ohgreat.id-Jawaban Sudut Dalam dan Sudut Luar Segitiga halaman 107 Sudut Segi Banyak (Poligon) Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 107. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 4 Menyelidiki Sifat-Sifat Bangun Geometri. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Sudut Segi Banyak (Poligon)

Sudut Dalam dan Sudut Luar Segitiga

Q.Gambar berikut dibentuk dari pengubinan segitiga-segitiga kongruen. Dari gambar ini, apa yang dapat disimpulkan tentang sudut-sudut segitiga? Selain itu, hubungan apa yang terbentuk antara garis ℓ dan m?

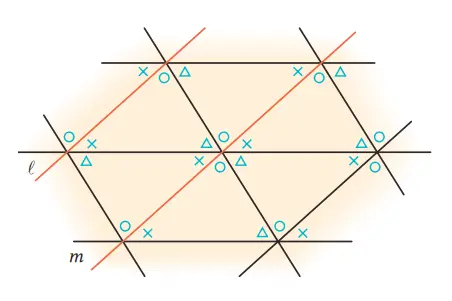
Jawaban:

Jumah 3 buah sudut segitiga adalah 180 derajat.
ℓ//m

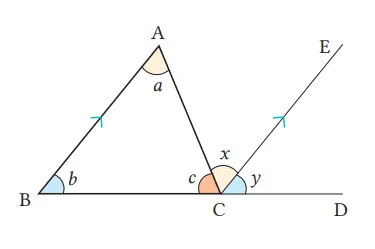
Pada gambar ∆ABC di sebelah kanan, sisi BC diperpanjang ke arah C sehingga terbentuk BD, dan garis CE dikonstruksi sejajar BA. Sudut-sudut dalam berseberangan yang terbentuk besarnya sama dan BA // CE, sehingga ∠a = ∠x.

Sudut-sudut sehadap yang terbentuk oleh garis-garis sejajar juga besarnya sama sehingga BA // CE dan ∠b = ∠y. Dengan demikian,

= ∠a + ∠b + ∠c

= ∠x + ∠y + ∠c = 180°

Berpikir Matematis

Kita dapat menunjukkan jumlah besar sudut-sudut segitiga 180° menggunakan sifat garis-garis sejajar.

Soal 1

Pada gambar di sebelah kanan, sudut manakah yang besarnya sama dengan ∠a + ∠b? Tunjukkan jawabanmu pada gambar, dan berilah penjelasan. Selain itu, tuliskan persamaannya dengan menggunakan bentuk aljabar.

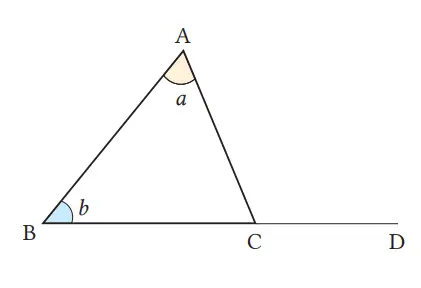
Jawaban:

Dari fakta bahwa jumlah ketiga sudut segitiga adalah 180°,

∠ACB = 180° – (∠a + ∠b) ①

Dari gambar,

∠ACB = 180° – ∠ACD ②

Dari ①, ②,

∠a + ∠b = ∠ACD

Soal 2

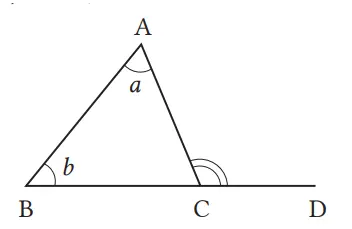
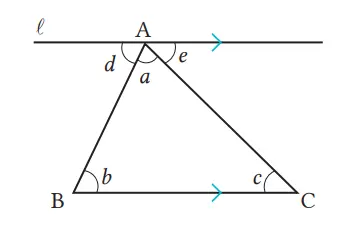
Jelaskan bahwa jumlah ketiga sudut ∆ABC adalah 180° dengan membuat garis ℓ sejajar sisi BC dan melalui titik A seperti ditunjukkan pada gambar.

Jawaban:

Karena sudut sehadap garis sejajar adalah sama, maka
∠b = ∠d, ∠c = ∠e

sehingga,

∠a + ∠b + ∠c
= ∠a + ∠d + ∠e
= 180°

Pada ∆ABC, ∠A, ∠B, dan ∠C disebut sudut-sudut dalam. Sudut-sudut yang terbentuk oleh sebuah sisi dan perpanjangan sisi, seperti ∠ACD atau ∠BCE disebut sudut-sudut luar pada titik C dari ∆ABC.

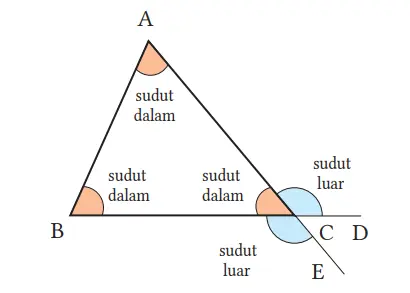
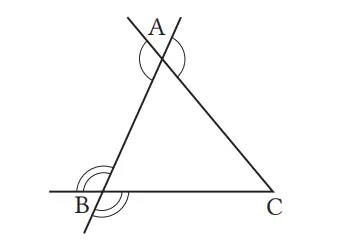
Soal 3

Pada ∆ABC pada gambar di atas, tunjukkan sudut-sudut luar di titik A dan B.

Jawaban:

Kita dapat merangkum sifat-sifat sudut dalam dan sudut luar segitiga seperti berikut.

Sifat-Sifat Sudut Segitiga

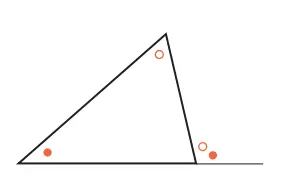
1. Jumlah sudut-sudut dalam segitiga adalah 180°.

2. Jumlah sudut luar segitiga sama dengan jumlah dua sudut dalam yang tidak berdampingan dengan sudut luar tersebut.

Soal 4

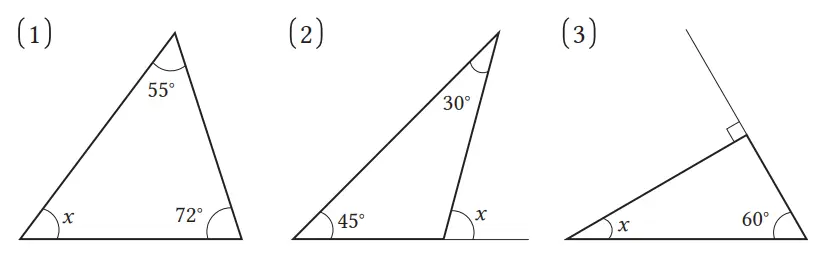
Carilah ∠x pada gambar-gambar berikut.

Jawaban:

(1) ∠x = 53°

(2) ∠x = 75°

(3) ∠x = 30°

Jumlah sudut-sudut dalam segitiga adalah 180°, adalah hal yang telah peserta didik pelajari sejak sekolah dasar sehingga telah mereka pahami dengan baik. Di sisi lain, sifat sudut luar segitiga sering dilupakan.

Dalam (2) dan (3), jika sifat sudut luar segitiga digunakan, maka dapat dengan mudah kita ketahui masing-masing, yaitu

(2) ∠x = 45° + 30° = 75°

(3) ∠x = 90° – 60° = 30°

Dalam situasi seperti itu, guru mengarahkan peserta didik untuk menyadari sifat sudut luar setiap kali mereka memiliki kesempatan.

Soal 5

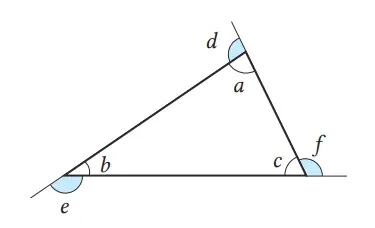
Berapakah jumlah sudut luar dari sebuah segitiga? Jelaskan dengan menggunakan sifat-sifat dari sudut-sudut segitiga.

Jawaban:

360°

⟨Alasan⟩

Pada sembarang titik sudut, jumlah sudut dalam dan satu sudut luar adalah 180°. Karena itu,

∠a + ∠d + ∠b + ∠e + ∠c + ∠f
= 180° × 3 = 540°

Karena jumlah sudut dalam segitiga adalah 180°,

jumlah sudut luar segitiga adalah

∠d + ∠e + ∠f = 540° – 180° = 360°

Catatan Jumlah sudut-sudut luar berarti jumlah dari sudut-sudut luar pada tiap titik sudut.

Sebagaimana kita ketahui dari penyelidikan di Soal 5, jumlah sudut-sudut luar segitiga adalah 360°.

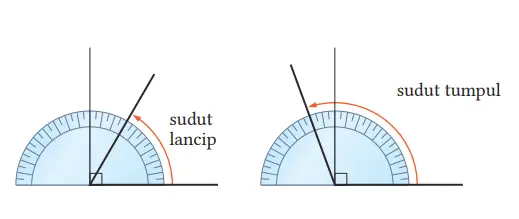
Sudut yang besarnya lebih dari 0° dan kurang dari 90° disebut sudut lancip. Sudut yang besarnya lebih dari 90° dan kurang dari 180° disebut sudut tumpul.

Segitiga dapat kita kelompokkan ke dalam tiga jenis berdasarkan sudut-sudut dalamnya.

1 Segitiga lancip: Besar ketiga sudut dalamnya lancip.

2 Sudut siku-siku: Besar salah satu sudut dalamnya 90°.

3 Segitiga tumpul: Besar salah satu sudut dalamnya tumpul.

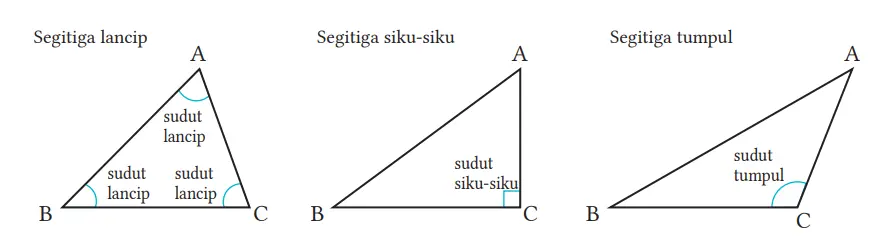
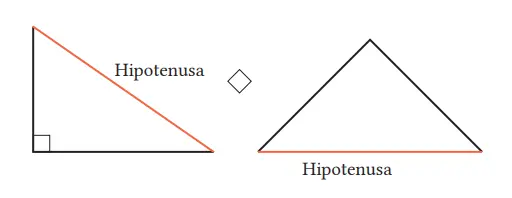
Sisi segitiga yang berada di depan sudut siku-siku disebut hipotenusa atau sisi miring.

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***