ohgreat.id-Jawaban Soal Garis dan Sudut halaman 164 Sifat-Sifat Dasar Bangun Datar Matematika SMP Kelas 7 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 164. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 5 Bangun Datar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Sifat-Sifat Dasar Bangun Datar
Garis dan Sudut
Siswa memahami bentuk-bentuk dasar seperti garis dan sudut.
Garis
Q. Pada gambar di samping, tariklah beberapa garis yang melewati A. Kemudian buatlah garis yang melalui A dan B.

Jawaban:
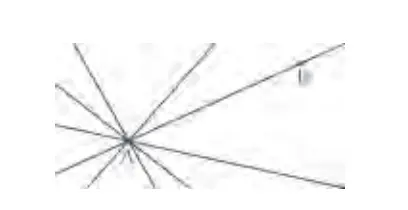
Jika kita menarik garis yang melewati A dan B, maka tidak ada garis lain yang juga melewati kedua titik A dan B. Namun, ada banyak garis yang melewati satu titik A. Dengan kata lain, hanya ada satu garis yang melalui dua titik A dan B. Sebuah garis yang melalui dua titik A dan B disebut garis AB.
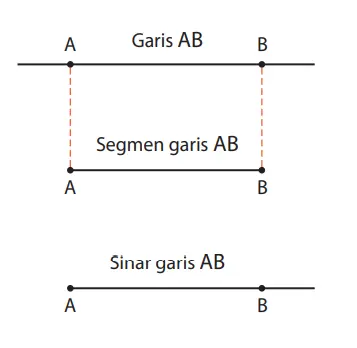
Jika kita mengatakan garis, yang dimaksud adalah garis lurus yang dapat perpanjang tak terhingga ke kedua arah. Untuk garis AB, bagian garis mulai dari A sampai B disebut ruas garis (segmen garis) AB. Garis lurus yang dapat perpanjang ke arah B mulai dari titik A disebut sinar garis AB.
1. Jika kita hubungkan tiga titik berbeda A, B, dan C pada gambar di samping kiri, bangun apa yang diperoleh?
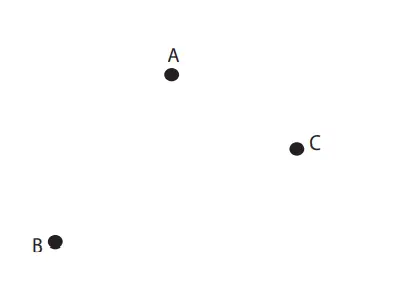
Jawaban:
Bangun segitiga
Kita menggunakan simbol ∆ dan menulis segitiga ABC sebagai ∆ABC. Kita baca “segitiga ABC”
Sudut
Q. Berapakah besar satu sudut segitiga sama sisi? Berapa besar satu sudut segi lima sama sisi diukur dalam derajat?
Jawaban:
Segitiga sama sisi… 60°
Segienam sama sisi… 120°
2. Bagian yang berwarna pada bangun di samping ini adalah ∠x dan sudut ∠y. Nyatakanlah sudut ∠x dan sudut ∠y menggunakan simbol dengan A, B, C, dan D berturut-turut.
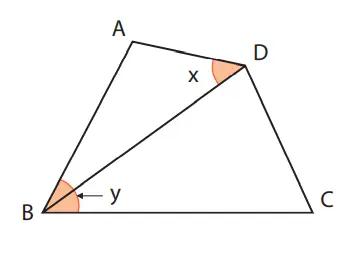
Jawaban:
∠x… ∠ADB atau ∠BDA
∠y… ∠ADC atau ∠CBA
3. Seperti pada gambar di samping ini, garis AB dan CD berpotongan di titik O. Jika sudut ∠AOC = 50° , tentukan ukuran sudut berikut.
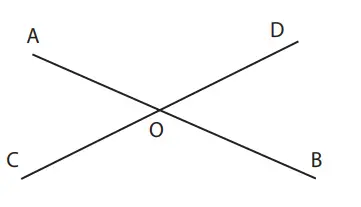
(1) ∠COB
Jawaban:
∠COB = 130°
(2) ∠DOB
Jawaban:
∠DOB = 50°
Tempat Kedudukan Relatif Dua Garis
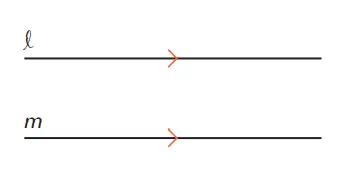
Q. Jika m diputar 360° dengan pusat O, seperti ditunjukkan gambar di samping ini, dapatkah kita simpulkan bahwa garis l dan m selalu berpotongan?
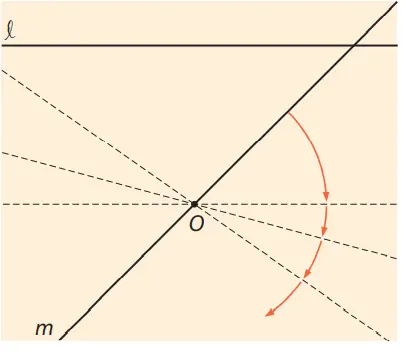
Jawaban:
Tidak dapat kita katakan selalu berpotongan
Kita menamakan garis dengan huruf kecil, seperti l atau m.
Dua garis pada bidang datar, kedudukannya berpotongan atau tidak berpotongan.
Jika sudut pada titik potong dua garis l dan m merupakan sudut siku-siku, maka kita katakan bahwa dua garis tersebut tegak lurus.
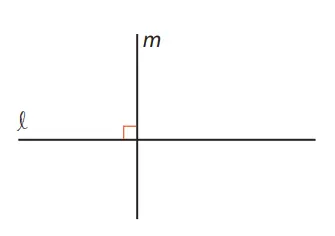
Kita menggunakan simbol ⊥ dan ditulis l ⊥ m. Kita baca “l tegak lurus m.” Jika dua garis tegak lurus, maka kita katakan garis yang satu tegak lurus pada garis yang lain.
Jika dua garis pada bidang tidak berpotongan, kita katakan bahwa garis l sejajar garis m. Kita menggunakan simbol l//m. Kita baca “l sejajar m.”
4. Pada gambar di sisi kiri ini, tariklah garis yang melalui titik P yang tegak lurus pada garis l. Tariklah garis yang melalui Q dan sejajar garis l.
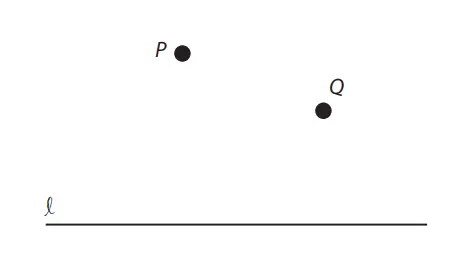
Jawaban:
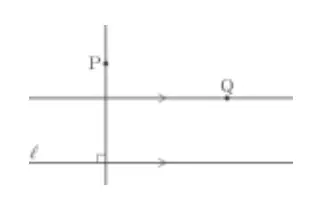
Jarak
Q. Pada gambar di samping kanan, manakah di antara titik A, B, H, dan C pada garis l yang panjangnya terpendek ke titik P? Selidiki dengan menggunakan jangka.
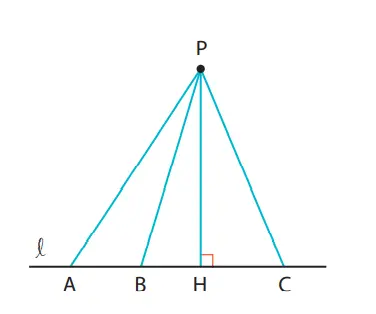
Jawaban:
Titik H
Menunjuk pada Q , ketika menggambar garis yang tegak lurus pada l melalui P yang berbeda dengan l, dan kita namai titik potongnya H, maka panjang segmen garis PH merupakan jarak antara titik P ke garis l.
5. Pada gambar di samping kanan, ditunjukkan bahwa l//m. Bandingkan tiga jarak berikut ini.
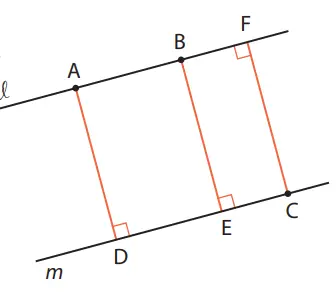
a. Jarak antara titik A yang berada di
garis l ke garis m.
b. Jarak antara titik B yang berada di
garis l ke garis m.
c. Jarak antara titik C yang berada di
garis m ke garis l..
Jawaban:
Berdasarkan gambar, karena l//m maka garis lurus l dan m tidak berpotongan, oleh karenanya AD = B E = CF. Oleh karenanya, jarak a, b, dan c semuanya sama.
Mari Mencoba
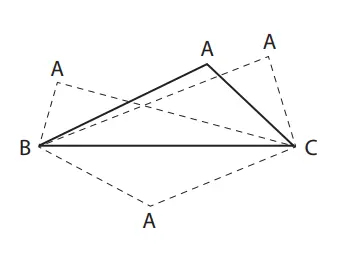
Dalam setiap ∆ABC, AB + AC > BC. Jelaskan fakta ini menggunakan jarak antara titik B dan C.
Jawaban:
Panjang segmen garis BC adalah sama dengan jarak di antara dua titik B dan C. Di sisi lain, panjang AB + AC menunjukkan panjang garis putus-putus yang menghubungkan 2 titik B dan C.
Oleh karenanya, di antara garis yang menghubungkan dua titik B dan C, panjang segmen garis BC adalah yang terpendek. Selain itu, karena titik A tidak berada pada segmen garis BC, maka terbentuklah AB + AC > BC.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***