
ohgreat.id-Jawaban Latihan Mandiri 8.4 halaman 230 Peluang Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMA/SMK Kelas 10 halaman 230. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMA/SMK Kelas 10 Kurikulum Merdeka Bab 8 Peluang. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Latihan Mandiri 8.4
Soal Pemahaman
1. Misalnya kalian melemparkan uang logam tiga kali.
a. Buatlah daftar ruang sampel untuk semua 8 hasil yang mungkin. Sebagai contoh, salah satu hasil adalah gambar, angka, angka (GAA).
Jawaban:
{(G, G, G), (G, G, A), (G, A, G), (A, G, G), (G, A, A), (A, G, A), (A, A, G),(A, A, A)}
b. Apakah hasil di dalam ruang sampel kalian sama besar kemungkinan terjadinya? Jelaskan.
Jawaban:
Ya. Masing-masing hasil di dalam ruang sampel ini sama besar kemungkinan terjadinya karena memiliki peluang yang sama, yaitu .
c. Buatlah tabel distribusi peluang untuk jumlah gambar. Apa peluang untuk mendapatkan tepat 2 gambar? Paling banyak 2 gambar?
Jawaban:

2. Yang manakah dari pasangan peristiwa berikut ini yang saling lepas? Jelaskan alasannya.
a. Melempar sepasang dadu: mendapatkan jumlah 6; mendapatkan satu dadu 6.
Jawaban:
Saling lepas karena jika salah satu dadu adalah angka 6, maka jumlahnyapasti lebih dari 6.
b. Melemparkan uang logam 7 kali: mendapatkan tepat 3 gambar; mendapatkan tepat 5 gambar.
Jawaban:
Saling lepas karena harus tepat 5 dan tepat 3.
c. Melemparkan uang logam 7 kali: mendapatkan setidaknya 3 gambar; mendapatkan setidaknya 5 gambar.
Jawaban:
Tidak saling lepas karena setidaknya 3 tercakup dalam setidaknya 5 sehingga ada irisan antara dua kejadian.
3. Gunakan bentuk yang sesuai dari aturan penjumlahan untuk menentukan peluang dari melempar sepasang dadu dan
a. mendapatkan jumlah 6 atau mendapatkan satu dadu dengan 6,
Jawaban:
P (jumlah 6 atau satu 6) = P (jumlah 6) + P (satu enam) = 5/36 + 10/36 = 15/36
b. mendapatkan jumlah 6 atau mendapatkan angka yang sama.
Jawaban:
P (jumlah 6 atau amgka sama) = P (jumlah 6) + P (satu enam) – P (jumlah 6 dan angka sama)= 5/36 + 6/36 – 1/36 = 10/36
Soal Aplikasi
4. Misalnya kalian melemparkan sebuah dadu dan kemudian melemparkannya kembali. Dadu berbentuk tetrahedron (limas segitiga) beraturan dan terdapat angka 1, 2, 3, dan 4 pada sisinya.
Gambar 8.5 Dadu Berbentuk Limas Segitiga
a. Buatlah bagan yang menunjukkan ruang sampel dari semua kemungkinan hasilnya.
Jawaban:
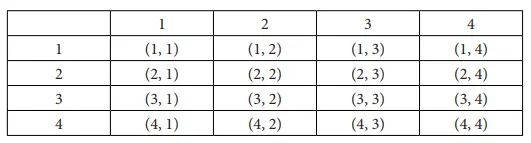
b. Ada berapa hasil kemungkinan? Apakah semua sama besar kemungkinannya?
Jawaban:
16 hasil kemungkinan dan sama besar kemungkinannya.
c. Buatlah tabel distribusi peluang untuk selisih dari kedua dadu (dadu pertama-dadu kedua). [Keterangan: Bukan nilai mutlak dari selisih]
Jawaban:
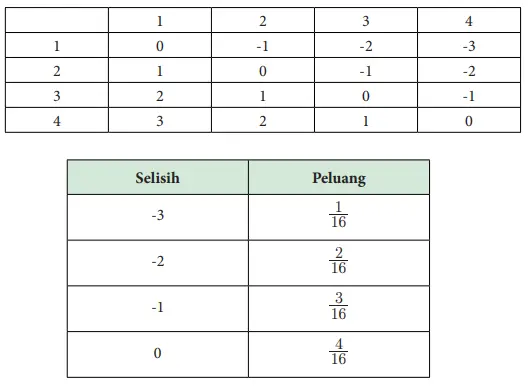
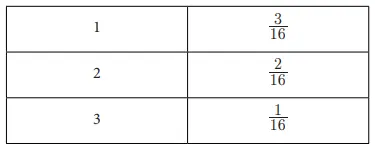
d. Selisih apa yang paling mungkin kalian dapatkan?
Jawaban:
Selisih 0
e. Berapa peluang bahwa selisihnya paling besar 2?
Jawaban:
1/16 + 2/16 + 3/16 + 4/16 + 3/16 + 2/16 = 15/16 atau 1 – 1/16 = 15/16
5. Misalnya kalian melemparkan dadu berbentuk tetrahedron (limas segitiga beraturan) dan sebuah dadu biasa (berbentuk kubus dengan enam sisi) pada saat yang sama.
a. Buatlah bagan yang menunjukkan ruang sampel dari semua hasil yang mungkin.
Jawaban:
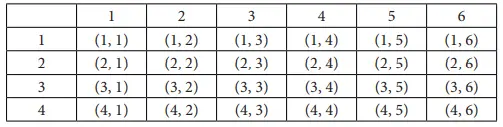
b. Berapa banyak hasil yang mungkin? Apakah semuanya sama besar kemungkinannya?
Jawaban:
Ada 24 hasil kemungkinan dan semua sama besar kemungkinannya.
c. Buatlah tabel untuk distribusi peluang dari jumlah kedua dadu.
Jawaban:
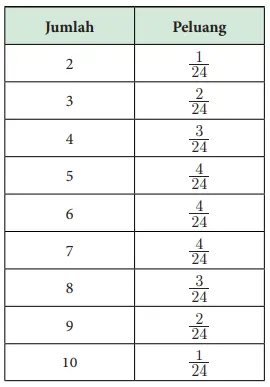
d. Jumlah apa yang paling mungkin didapat?
Jawaban:
Jumlah 5, 6, 7 memiliki peluang paling besar yaitu masing-masing 4/24.
e. Berapa peluang bahwa jumlahnya paling banyak 3?
Jawaban:
1/24 + 2/24 = 3/24
6. Gunakan hasil kerja kalian pada soal 4 dan bentuk yang sesuai dari aturan penjumlahan untuk menjawab pertanyaan berikut yang berhubungan dengan melempar dua dadu tetrahedron.
a. Berapa peluang kalian mendapatkan perbedaan 3 atau mendapatkan 2 pada dadu pertama?
Jawaban:
Saling lepas. P = 2/16 + 4/16 = 6/16 = 3/8
b. Berapa peluang mendapatkan selisih 2 atau mendapatkan angka yang sama?
Jawaban:
Saling lepas. P = 4/16 + 4/16 = 8/16 = 1/2
c. Berapa peluang mendapatkan selisih 0 atau mendapatkan angka yang sama?
Jawaban:
Tidak saling lepas. P= 4/16 + 4/16 – 4/16 = 4/16 = 1/4
d. Berapa peluang mendapatkan selisih 0 atau jumlah 6?
Jawaban:
Tidak saling lepas. P= 4/16 + 3/16 – 1/16 = 6/16 = 3/8
Soal Penalaran
7. Untuk kasus dua dadu dilempar dua kali, pertimbangkan peluang mendapatkan dua angka yang sama pada lemparan pertama atau pada lemparan kedua.
a. Apakah benar bahwa peluang mendapatkan dua angka yang sama pada lemparan pertama atau pada lemparan kedua adalah ? Berikan penjelasan untuk jawaban kalian.
Jawaban:
Peluang mendapatkan angka yang sama untuk lemparan pertama adalah 1/6 yang merupakan kemungkinan yang cukup kecil. Demikian juga peluangmendapatkan angka yang sama pada lemparan kedua adalah 1/6. Sangat tidakmasuk akal jika peluang mendapatkan dua hasil ini menjadi lebih besar.Untuk guru: dua kejadian ini disebut saling bebas, dan akan dipelajari di kelas 11.
b. Apakah benar bahwa peluang mendapatkan dua angka yang sama pada setidaknya satu dari enam giliran adalah?
Jawaban:
Cara berpikir sama dengan 7a yaitu sangat tidak masuk akal jika peluangnya menjadi 1, yang artinya pasti terjadi. Padahal, justru kemungkinannya seharusnya semakin kecil mendapatkan angka yang sama berturut-turut sebanyak 6 kali.
8. Misalnya kalian melemparkan uang logam empat kali dan mencatat gambar (G) atau angka (A) sesuai urutan munculnya.
a. Buatlah daftar semua 16 hasil yang mungkin.
Jawaban:
{(GGGG), (GGGA), (GGAG), (GAGG), (AGGG), (GGAA), (GAGA), (GAAG), (AGGA), (AGAG), (AAGG), (GAAA), (AGAA), (AAGA),(AAAG), (AAAA)}
b. Apakah hasil ini sama besar kemungkinannya?
Jawaban:
Ya
c. Buatlah tabel distribusi peluang untuk jumlah gambar.
Jawaban:
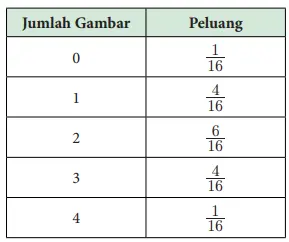
d. Berapa peluang yang kalian dapatkan tepat 2 gambar? Paling banyak 2 gambar?
Jawaban:
P (tepat 2 gambar) = 6/16 : P(paling banyak 2 gambar) = 1/16 + 4/16 + 6/16 = 11/16
9. Perhatikan dadu khusus yang ditunjukkan sisi-sisinya sebagai berikut. Misalnya dalam sebuah permainan kalian memilih salah satu dadu, dan teman kalian memilih satu dari sisanya. Masing-masing melemparkan dadunya. Yang mendapatkan angka yang lebih besar memenangkan permainan.
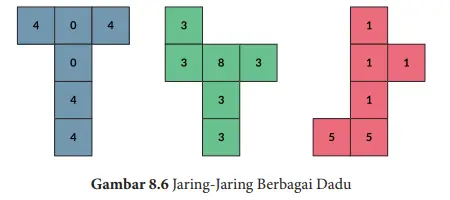
Misalnya teman kalian memilih dadu biru. Supaya kesempatan menang lebih besar, dadu mana yang kalian akan pilih? Jika teman kalian memilih dadu hijau, dadu mana yang kalian akan pilih? Jika teman kalian memilih dadu merah, dadu mana yang kalian akan pilih? Apa kejutan di sini?
Jawaban:
Selanjutnya untuk menentukan dadu mana yang memiliki peluang lebih besar menang, dapat dibuat tabel-tabel sebagai berikut:
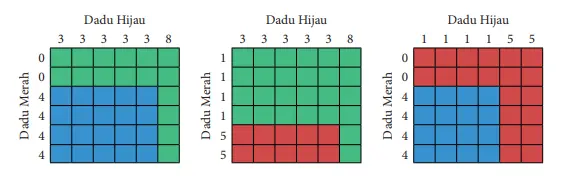
Apabila teman memilih dadu biru, maka dadu merah memiliki peluang lebih besar untuk menang. Dan jika teman memilih dadu hijau, maka dadu biru memiliki peluang lebih besar untuk menang. Selanjutnya jika teman memilih dadu merah, maka dadu hijau memiliki peluang lebih besar untuk menang. Kejutannya adalah tidak ada satu dadu yang pasti selalu menang.
10. Pikirkan tiga kejadian A, B dan C.
a. Gambarlah diagram Venn yang menyatakan situasi di mana A dan B adalah saling lepas, A dan C adalah saling lepas, dan B dan C adalah saling lepas.
b. Gambarlah diagram Venn yang menyatakan situasi di mana A dan B adalah saling lepas, A dan C adalah saling lepas, tetapi B dan C tidak saling lepas.
c. Gambarlah diagram Venn yang menyatakan situasi di mana A dan B tidak saling lepas, A dan C tidak saling lepas, dan B dan C tidak saling lepas.
Jawaban
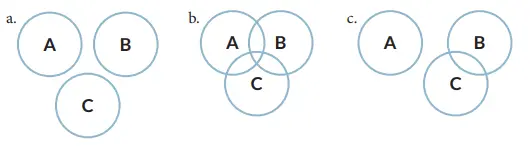
Selanjutnya gunakan diagram yang sesuai untuk membantu kalian menuliskan sebuah aturan penjumlahan yang kalian dapat gunakan untuk menentukan ketika
d. A dan B adalah saling lepas, A dan C adalah saling lepas, dan B dan C adalah saling lepas.
Jawaban:
P (A ∪ B ∪ C) = P (A) + P (B) + P(C) – P(B ∩ C)
e. A dan B adalah saling lepas, A dan C adalah saling lepas, tetapi B dan C tidak saling lepas.
Jawaban:
P (A ∪ B ∪ C) = P (A) + P (B) + P(C) – P(B ∩ C)
f. A dan B tidak saling lepas, A dan C tidak saling lepas, dan B dan C tidak saling lepas.
Jawaban:
P (A ∪ B ∪ C) = P (A) + P (B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***






