
ohgreat.id-Jawaban Jumlah Sudut Dalam Segi Banyak halaman 110 Sudut Segi Banyak (Poligon) Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 110. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 4 Menyelidiki Sifat-Sifat Bangun Geometri. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Sudut Segi Banyak (Poligon)
Jumlah Sudut Dalam Segi Banyak
Q.Mari kita cari jumlah sudut-sudut dalam dari sebuah pentagon (segi lima). Jelaskan!
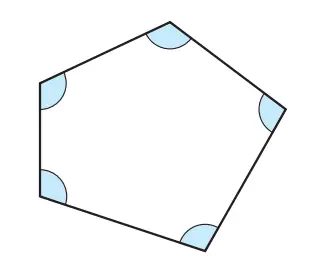
Jawaban:
Jika Anda menggambar dua garis diagonal dari satu titik sudut, Anda dapat membaginya menjadi tiga segitiga. Oleh karena itu, jumlah sudut interior segi lima adalah 180° × 3 = 540°
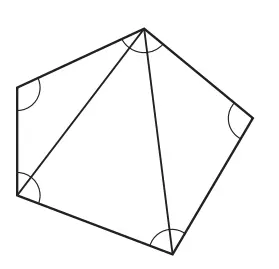
1. Pada Q, Heru menemukan jumlah sudut-sudut dalam sebuah pentagon (segi lima). Jelaskan!
Cara Heru
Segi lima dapat dibagi ke dalam tiga segitiga dengan menarik diagonal-diagonal dari salah satu titik sudut, sehingga jumlah sudut dalamnya adalah 3 × 180° = 540°
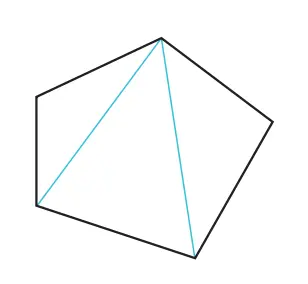
Lengkapi tabel berikut dengan mengikuti Cara Heru dan tentukanlah jumlah sudut-sudut dalam dari berbagai segi banyak.
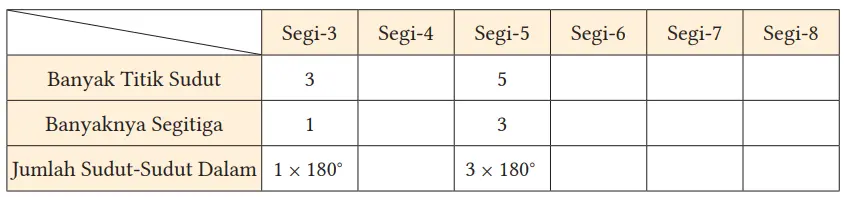
Jawaban:
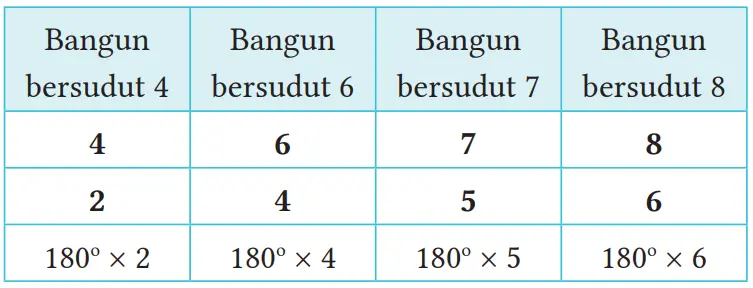
2. Dari tabel 1 , apakah hubungan antara banyaknya titik sudut dan banyaknya segitiga? Bentuk aljabar apa yang dapat digunakan untuk menentukan jumlah sudut-sudut dalam sebuah segi-10?
Jawaban:
Jumlah yang telah dikurangi 2 dari jumlah simpul poligon, akan menjadi jumlah segitiga. Jumlah dari sudut dalam dari bangun bersudut sepuluh adalah 180° × (10 – 2) = 1.440°
3. Pada bagian 1 di halaman sebelumnya, jika kita misalkan n adalah banyaknya titik sudut segi banyak, bentuk aljabar seperti apa yang dapat digunakan untuk menentukan jumlah sudut-sudut dalam dari sebuah segi banyak?
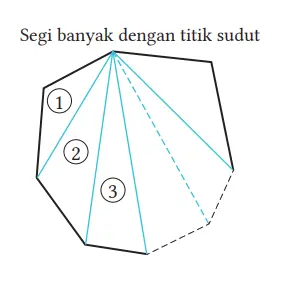
Jawaban:
180° × (n – 2)
Dari hasil penyelidikan kita sejauh ini, jumlah sudut-sudut dalam dari segi banyak dengan n titik sudut dapat merangkumnya sebagai berikut.
Jumlah Sudut-Sudut Dalam Segi Banyak
Jumlah sudut-sudut dalam segi banyak dengan n titik sudut adalah (n – 2) × 180°.
4. Pada di halaman sebelumnya, Dewi menemukan jumlah sudut-sudut dalam dari segi-5 sebagai berikut.
Cara Dewi
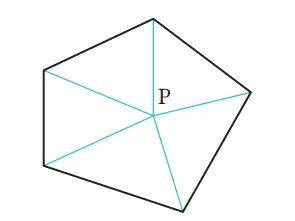
Ambil titik P di dalam segi-5 dan hubungkan ke tiap titik sudut, sehingga jumlah sudut-sudut dalamnya adalah 5 × 180° – 360° = 540°
Jawaban:
Karena dibagi menjadi lima segitiga, maka jumlah sudut dalamnya adalah 180° × 5 = 900°
Dengan mengurangi 360° , jumlah sudut di sekitar titik internal P, dari 900° ini, 900° – 360° = 540°
5. Dengan menggunakan Cara Dewi, tentukan jumlah sudut dalam segi banyak dengan n titik sudut, dan tunjukkan bahwa besarnya adalah (n – 2) × 180°.
Jawaban:
Jika mencarinya dengan Cara Dewi, 180° × n – 360°
Di samping itu, 180° × (n – 2)
= 180° × n – 180° × 2
= 180° × n – 360°
Oleh karena itu, 180° × n – 360° sama dengan 180° × (n – 2).
6. Jawablah pertanyaan-pertanyaan berikut bila diketahui jumlah sudut dalam sebuah segi banyak dengan titik sudut n adalah (n – 2) × 180°.
(1) Berapakah jumlah sudut dalam segi-12?
Jawaban:
180° × (12 – 2) =1800°
(2) Berapakah besar sebuah sudut dalam dari segi-12 beraturan?
Jawaban:
1800° : 12 = 150°
(3) Segi banyak mana yang jumlah sudut dalamnya 1.260°.
Jawaban:
Jika poligon yang dicari adalah bangun bersudut n, 180° × (n – 2) = 1260°
n – 2 = 7
n = 9
Jawaban: Nonagon
Cermati
Berpikir dengan Mengitari Titik P
Ketika kita menemukan jumlah sudut-sudut dalam segi-5, kita membagi segi-5 tersebut ke dalam segitiga-segitiga dengan cara berikut.
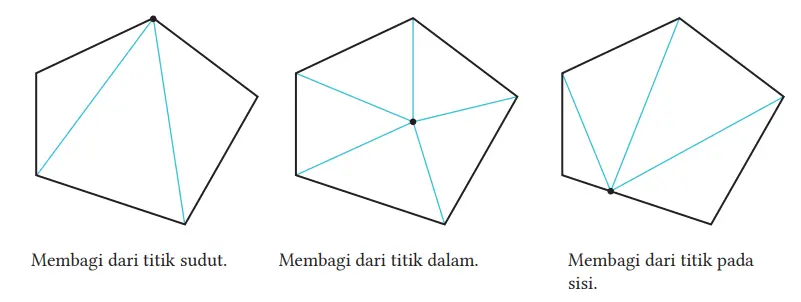
Jika kita berpikir cara-cara ini sebagai “menghubungkan sembarang titik P ke setiap titik sudut segi-5 dan menggerakkan P ke yang lain”, maka kita akan melihat cara-cara tersebut sebagai satu kesatuan ide.
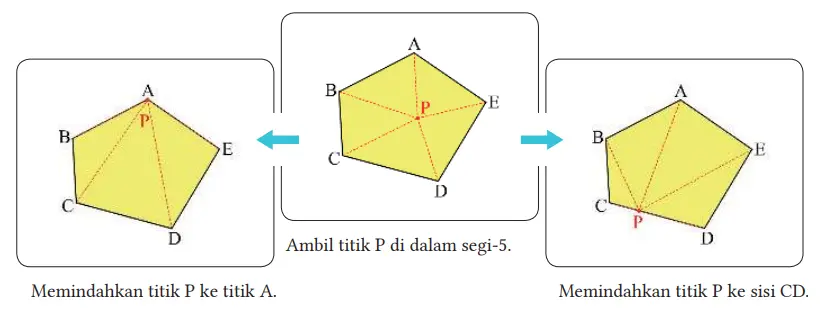 Jika kita memiliki gagasan ini, kita dapat berpikir untuk memindahkan titik P ke luar dari segi-5. Gunakan gambar di samping untuk menentukan jumlah sudut-sudut dalam dari segi-5.
Jika kita memiliki gagasan ini, kita dapat berpikir untuk memindahkan titik P ke luar dari segi-5. Gunakan gambar di samping untuk menentukan jumlah sudut-sudut dalam dari segi-5.
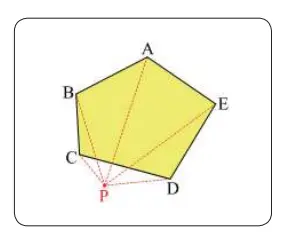
Jawaban:
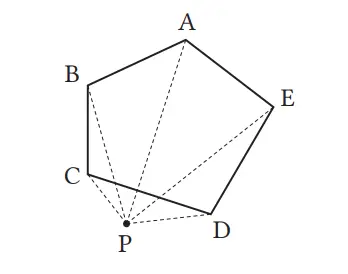
Cukup dengan mengurangi 180° jumlah sudut dalam ΔPDC, dari jumlah sudut dalam keempat segitiga ΔPBC, ΔPAB, ΔPEA, dan ΔPDE. Sehingga, jumlah sudut dalam segi lima adalah 180° × 4 – 180o = 540°
.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***






