ohgreat.id-Jawaban Bentuk Penyajian Fungsi halaman 175 Memahami Fungsi Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman175. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 4 Relasi dan Fungsi. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Relasi dan Fungsi

Memahami Fungsi

Bentuk Penyajian Fungsi

Ayo Bereksplorasi

Berikut ini adalah ketentuan tarif yang diberlakukan oleh perusahaan taksi:

1. Biaya tarif awal sebesar Rp7.500,00 dan tarif per kilometer sebesar Rp3.000,00.

2. Berapa besar tarif yang dibutuhkan untuk perjalanan sejauh 20 km, 25 km, 30 km?

3. Dapatkah kalian menetapkan tarif untuk perjalanan sejauh 36 km?

Sejauh berapa kilometer yang dibutuhkan untuk uang sebesar Rp154.500,00.

Hitungan aritmetika:

a. Untuk biaya 20 km = Rp7.500,00 + 20 × Rp3.000,00 = Rp67.500,00

b. Untuk biaya 25 km = Rp7.500,00 + 25 × Rp3.000,00 = Rp82.500,00

c. Untuk biaya 30 km = Rp7.500,00 + 30 × Rp3.000,00 = Rp97.500,00

Bagaimanakah cara kalian menentukan rumus fungsinya?

Sekarang, coba kalian perhatikan dengan cermat beberapa cara berikut dalam menyajikan fungsi yang sering digunakan dalam matematika, sebelum menghitung rumus fungsi.

Misalkan suatu fungsi f diterapkan dari himpunan P = {1, 2, 3, 4, 5} ke himpunan Q = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. “setengah kali dari” merupakan relasi yang ditentukan.

Masalah ini dapat dinyatakan dalam lima cara, yaitu berikut ini.

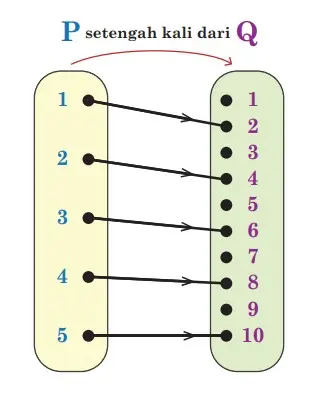
Cara Pertama: Diagram Panah

Misalkan suatu fungsi f dihubungkan dari himpunan P ke Q dengan anggota masing-masing P = {1, 2, 3, 4, 5} dan Q = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Selanjutnya apabila “setengah kali dari” adalah relasi yang ditentukan, maka diagram berikut ini merupakan cara yang dapat digunakan untuk hubungan tersebut.

Cara kedua: Himpunan Pasangan Berurutan

Misalkan suatu fungsi f dihubungkan dari himpunan P ke Q dengan anggota masing-masing P = {1, 2, 3, 4, 5} dan Q = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Apabila “setengah kali dari” adalah relasi yang ditentukan, maka himpunan pasangan berikut ini merupakan cara yang dapat digunakan untuk hubungan tersebut.

f = {(1,2);(2,4);(3,6);(4,8);(5,10)}

Cara ketiga: Persamaan Fungsi

Misalkan suatu fungsi f dihubungkan dari himpunan P ke Q dengan anggota masing-masing P = {1, 2, 3, 4, 5} dan Q = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Apabila “setengah kali dari” adalah relasi yang ditentukan, maka rumus fungsi berikut ini merupakan cara yang dapat digunakan untuk hubungan tersebut.

Perhatikan pola berikut untuk direpresentasikan dengan menggunakan rumus fungsi. Selanjutnya himpunan pasangan berurutan dari {(1, 2); (2, 4); (3, 6); (4, 8); (5, 10)} dapat membentuk menjadi pola matematika sebagai berikut.

(1, 2) menjadi (1,2 x 1)

(2, 4) menjadi (2,2 x 2)

(3, 6) menjadi (3,2 x 3)

(4, 8) menjadi 4,2 x 4)

(5, 10) menjaidi (5,2 x 5)

Pengertian:

Apabila anggota himpunan P disebut sebagai simbol x dan anggota himpunan Q disebut sebagai simbol y, maka didapat persamaan x = ½y. Selanjutnya persamaan ini x = ½y dapat diubah menjadi persamaan y= 2x , bentuk persamaan seperti ini dapat kita tulis dengan notasi dan rumus fungsi seperti berikut ini:

1. Notasi fungsi; f : x → y atau f : x → f(x) atau f : x → 2x

2. Rumus fungsi; f (x) = 2x, untuk setiap x ∈ P

Bentuk seperti inilah yang disebut sebagai persamaan fungsi.

Ayo Berpikir Kritis

Herman mengatakan bahwa setiap fungsi pasti bisa dituliskan rumus fungsinya. Sedangkan Ida mengatakan bahwa setiap fungsi belum tentu bisa dituliskan rumus fungsinya. Mereka berdua sepakat bahwa pendapatnya adalah benar. Setujukah kalian dengan salah satu pendapat dari meraka? Jelaskan.

Berikut Alternatif Jawaban “Ayo Berpikir Kritis” yang Bernilai Benar.

Setiap fungsi belum tentu bisa dituliskan rumus fungsinya, misalkan relasi tentang pemilik nomor HP, Anak dari, Ibu Kota suatu Negara, dan lainnya.

Langkah-langkah Kegiatan Berpikir Kritis ini diserahkan sepenuhnya kepada teman Guru untuk menyusunnya sendiri, sebagai latihan. Kemudian perkirakan sendiri juga kesimpulan yang didapat.

Cara keempat: Tabel

Misalkan suatu fungsi f dihubungkan dari himpunan P ke Q dengan anggota masing-masing P = {1, 2, 3, 4, 5} dan Q = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Selanjutnya apabila “setengah kali dari” adalah relasi yang ditentukan, maka tabel berikut ini merupakan cara yang dapat digunakan untuk hubungan tersebut.

x = 1, 2, 3, 4, 5

f(x) = 2, 4, 6, 8

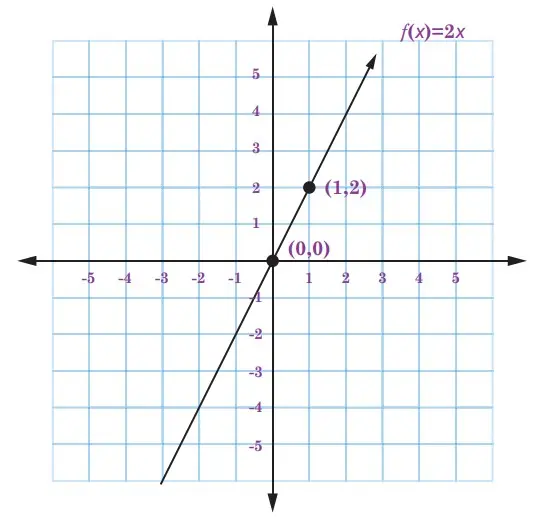
Cara kelima: Graik

Misalkan suatu fungsi f dihubungkan dari himpunan P ke Q dengan anggota masing-masing P = {1, 2, 3, 4, 5} dan Q = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Apabila “setengah kali dari” adalah relasi yang kita tentukan, maka graik berikut ini merupakan cara yang dapat digunakan untuk hubungan tersebut.

Berdasarkan pembahasan di halaman sebelumnya, menunjukkan bahwa ada ada lima cara untuk menyatakan suatu fungsi dari himpunan P ke Q.

Kemudian, kembali ke masalah awal penentuan rumus fungsi untuk masalah tarif taksi yang kita bahas di atas.

Beberapa harga sewa taksi lah tersampaikan sebelumnya, selanjutnya akan kita tunjukkan lebih rinci seperti uraian berikut ini.

a. Besar biaya untuk 20 km = Rp7.500,00 + 20 × Rp3.000,00 = Rp67.500,00

b. Besar biaya untuk 25 km = Rp7.500,00 + 25 × Rp3.000,00 = Rp82.500,00

c. Besar biaya untuk 30 km = Rp7.500,00 + 30 × Rp3.000,00 = Rp97.500,00

Cobalah perhatikan dengan cermat terhadap angka yang muncul di setiap persamaan berikut:

a. Besar biaya untuk 20 km = Rp7.500,00 + 20 × Rp3.000,00

b. Besar biaya untuk 25 km = Rp7.500,00 + 25 × Rp3.000,00

c. Besar biaya untuk 30 km = Rp7.500,00 + 30 × Rp3.000,00

Perhatikan angka 20 di sebelah kiri dan angka 20 di sebelah kanan. Apa persamaan dan perbedaannya?

Perhatikan angka 7500 di sebelah kanan.

Untuk memastikannya, coba buat dan lengkapi Tabel 4.7 berikut.

Tabel 4.7 Besar Tarif Mobil Taksi

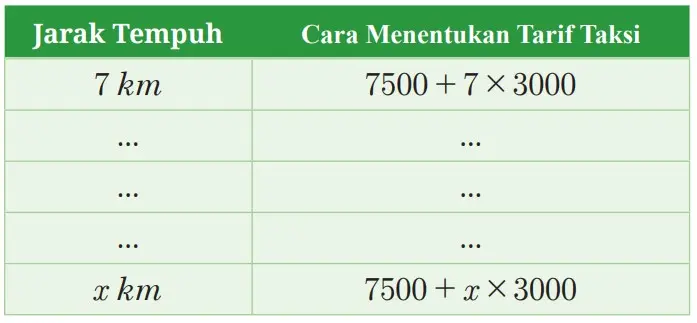
Jika B(x) adalah tarif naik taksi untuk x kilometer, maka B(x) dapat menyatakannya sebagai persamaan B (x) = + 3000 7500 x .

Ayo Berpikir Kritis

Bentuk diagram panah, himpunan pasangan berurutan, persamaan fungsi, tabel, dan graik adalah lima bentuk representasi fungsi yang paling populer dalam Matematika. Kelima cara menyajikan fungsi tersebut tidak harus menggunakannya untuk  setiap mengerjakan suatu soal, akan tetapi tergantung pertanyaan yang diminta dalam soal tersebut. Jailani mengatakan bahwa setiap fungsi pasti dapat menyatakannya  dengan kelima cara penyajian fungsi. Sedangkan Karim mengatakan bahwa setiap fungsi belum tentu dapat menyatakannya dengan kelima cara penyajian fungsi. Mereka berdua sepakat bahwa pendapatnya adalah benar. Setujukah kalian dengan salah satu pendapat dari meraka? Jelaskan.

Berikut Alternatif Jawaban Ayo Berpikir Kritis yang Bernilai Benar.

Setiap fungsi belum tentu dapat dinyatakan dengan kelima cara penyajian fungsi

Selanjutnya langkah-langkah Kegiatan Berpikir Kritis ini serahkan sepenuhnya kepada teman Guru untuk menyusunnya sendiri, sebagai latihan. Kemudian perkirakan sendiri juga kesimpulan yang didapat.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Selanjutnya Jangan lewatkan dan dapatkan Berita berita Update lainnya.***