ohgreat.id-Banyak Korespondensi Satu-satu halaman 194 Korespondensi Satu-satu (Pengayaan) Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 194. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 4 Relasi dan Fungsi. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Relasi dan Fungsi

Korespondensi Satu-satu (Pengayaan)

Banyak Korespondensi Satu-satu

Ayo Bereksplorasi

Simak dengan cermat penjelasan berikut untuk mempelajari lebih lanjut tentang korespondensi satu-satu.

Apabila diketahui anggota himpunan A adalah {1, 2, 3} dan anggota himpunan B adalah {a, b, c}. Relasi dari himpunan A ke B yang mungkin dapat dibentuk sebagai korespondensi satu-satu dapat diilustrasikan pada Tabel 4.8 berikut.

Tabel 4.8 Diagram Banyak Korespondensi Satu-Satu

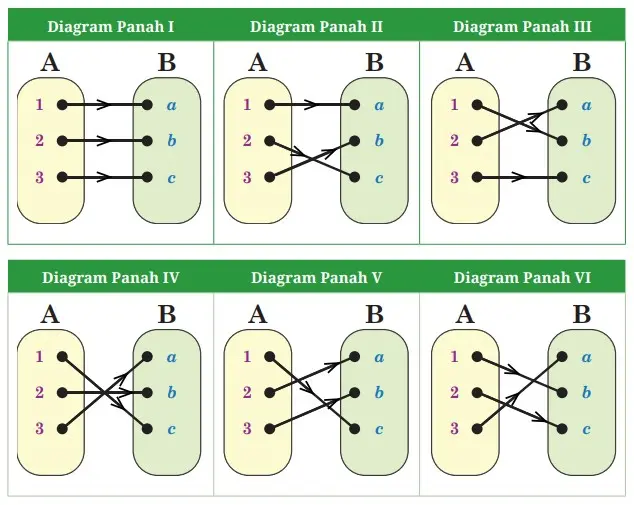
Berdasarkan sajian diagram panah pada Tabel 4.8 di atas, menunjukkan bahwa ada sebanyak 6 susunan diagram panah yang berbeda untuk korespondensi satu-satu dari himpunan A ke himpunan B.

Ayo Bekerja Sama

Berdasarkan temuan kalian pada Tabel 4.8, coba latihan pada Tabel 4.9 untuk menentukan berapa banyak korespondensi satu-satu yang ada antara himpunan A dan B tergantung pada jumlah anggota dan untuk menentukan berapa banyak orang yang diperlukan untuk membuat diagram panah penghubung himpunan A dan B. Berikut adalah contoh yang mungkin terjadi dan ditunjukkan pada Tabel 4.9. Sekarang, Cobalah kalian lengkapi isi sel yang masih kosong.

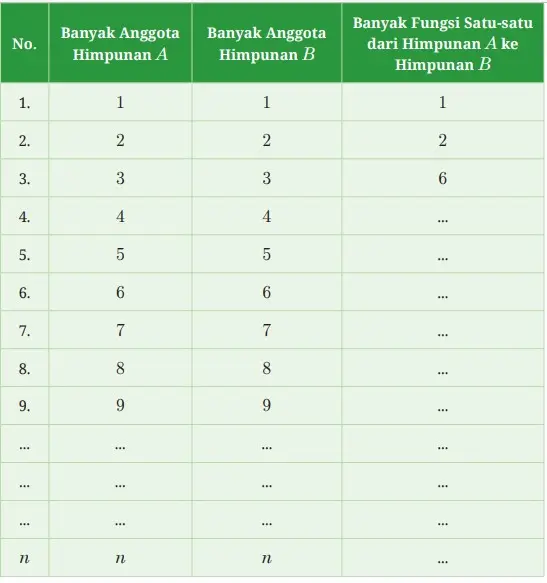
Tabel 4.9 Banyaknya korespondensi satu-satu

Ayo Berkomunikasi

Berdasarkan Tabel 4.8 dan 4.9 di halaman sebelumnya, dapat disimpulkan bahwa apabila banyak anggota himpunan A sama dengan banyak anggota himpunan B, yakni n(A) = n(B) = n; maka banyak korespondensi satu-satu yang mungkin dapat dibuat dari himpunan A ke himpunan B adalah sebanyak n! atau n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1.

Cobalah kalian perhatikan kesimpulan tersebut, apa yang perlu ditambahkan agar kesimpulan itu lebih komunikatif lagi?

Kemudian, sebutkan apa saja ciri-ciri dari dua himpunan dapat dikatakan korespondensi satu-satu atau tidak? Selanjutnya, dalam kondisi bagaimana dua himpunan tidak dapat dipastikan dikatakan korespondensi satu-satu? Jelaskan.

Sekarang, cobalah selesaikan kasus berikut ini untuk menunjukkan mengetahui pemahaman kalian.

Perhatikan dengan cermat pada diagram panah berikut ini.

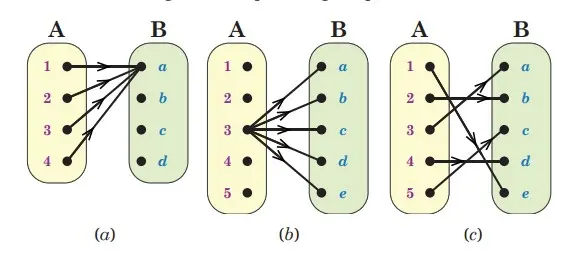
Gambar 4.13 diagram panah dari himpunan A ke himpunan B

1. Apakah relasi tersebut merupakan korespondensi satu-satu dari himpunan A ke himpunan B? Jelaskan.

2. Apabila relasi tersebut bukan merupakan korespondensi satu-satu, apakah diagram pada pada Gambar 4.13 termasuk fungsi? Jelaskan.

Berikut Alternatif Jawaban yang Bernilai Benar.

Dikarenakan pada contoh korespondensi satu-satu, jumlah kedua himpunannya adalah sama, maka untuk mengetahui jumlah anggotanya cukup untuk menentukan berapa banyak korespondensi satu-satu yang ada dari himpunan A ke himpunan B. Banyaknya anggota kemudian difaktorisasi; misalnya, jika ada 4 anggota, maka banyak korespondensi satu-satu yang mungkin terjadi adalah 4! = 4 × 3 × 2 × 1 = 24.

1. Karena tiga anggota himpunan B tidak ada pasangannya dan satu anggota himpunan B berpasangan lebih dari satu anggota himpunan A, maka diagram pada Gambar 4.12(a) (Buku Siswa) tidak menggambarkan korespondensi satu-satu. Di sisi lain, diagram dapat dianggap sebagai fungsi.

2. Karena satu anggota himpunan A dipasangkan lebih dari satu anggota himpunan A dan karena anggota himpunan A lainnya tidak memiliki pasangan, maka Gambar 4.14(b) (Buku Siswa) tidak merepresentasikan korespondensi satu-satu. Selain itu, diagram bukan fungsi.

3. Karena jumlah anggota yang identik di kedua himpunan dan fakta bahwa setiap anggota di kedua himpunan memiliki tepat satu pasangan, maka Gambar 4.14(c) (Buku Siswa) dapat dikatakan sebagai korespondensi satu-satu. Sehingga diagram termasuk fungsi.

Kemudian, mintalah siswa untuk memahami contoh 4.13 dan 4.14. Mintalah siswa untuk membagikan tugas mereka kepada rekan-rekan mereka, dan pastikan teman yang menerima tugas mengetahui apa yang harus diselesaikan. Selanjutnya periksa bagaimana mereka melakukan tugas mereka dan pastikan bahwa bahasa yang mereka gunakan sesuai dengan prinsip-prinsip moral yang baik.

Contoh 4.13

Apabila diketahui anggota himpunan K adalah {a, b, c, d, e} dan anggota himpunan L adalah {1, 2, 3, 4, 5}, tentukanlah banyaknya korespondensi satu-satu yang mungkin dari himpunan K ke himpunan L.

Alternatif penyelesaian

Diketahui himpunan K = {a, b, c, d, e} dan himpunan L = {1, 2, 3, 4, 5}, sehingga didapat banyak anggotanya adalah n(K) = 5 dan n(L) = 5

Jadi, banyaknya korespondensi satu-satu dari himpunan K ke himpunan L adalah sebanyak

n(K)! = n(L)! = 5!

5! = 5 × 4 × 3 × 2 × 1 = 120.

Contoh 4.14

Diketahui himpunan M = {x | -3 < x < 4, x bilangan bulat} dan himpunan N = {x | x < 7, x bilangan asli}. Tentukanlah banyaknya korespondensi satu-satu dari himpunan M ke himpunan N.

Alternatif penyelesaian

Diketahui M = {x | -3 < x < 4, x bilangan bulat} danN = {x | x < 7, x bilangan asli} M = {-2, -1, 0, 1, 2, 3} dan N = {1, 2, 3, 4, 5, 6} sehingga didapat n(M) = 6 dan n(N) = 6

Jadi, banyak korespondensi satu-satu yang mungkin dari himpunan M ke himpunan N adalah sebanyak n(M)! = n(N)! = 6!

6! = 6 × 5 × 4 × 3 × 2 × 1 = 720.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***