ohgreat.id-Jawaban Mengorganisasikan Data halaman 237 Bagaimana Menyelidiki Kecenderungan Data Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 237. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 7 Menggunakan Data. Selanjutnya pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Bagaimana Menyelidiki Kecenderungan Data

Mengorganisasikan Data

Siswa memahami perbedaan kecenderungan dua kumpulan data.

Jangkauan

Q. Pada Tabel 2, data posisi tangkapan penggaris siswa Kelas A dan Kelas B disusun berdasarkan panjangnya. Tentukan perbedaan antara data terkecil dan terbesar dalam setiap kelas. Berdasarkan Tabel 2, nilai terbesar data Kelas A adalah 15, 5 cm dan nilai terkecilnya adalah 8,0 cm.

Tabel 2： Data posisi tangkapan penggaris (cm)

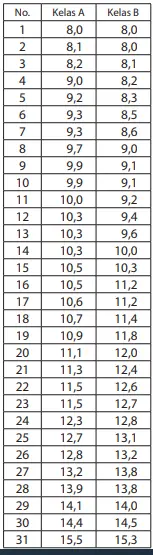
Jawaban:

a. Kelas A: 7,5 cm dari 15,5 – 8,0 = 7,5

b. Kelas B: 7,3 cm dari 15,3 – 8,0 = 7,3

Kita dapat menggunakan perbedaan nilai terbesar dan terkecil untuk menyatakan penyebaran (dispersi) data. Nilai ini disebut jangkauan data.

Jangkauan data Kelas A adalah 7,5 cm, karena 15,5 – 8,0 = 7,5

 

1. Berdasarkan Tabel 2, temukan nilai terbesar dan terkecil, serta jangkauan data Kelas B. Selanjutnya, bagaimana jika dibandingkan dengan jangkauan data Kelas A?

Jawaban:

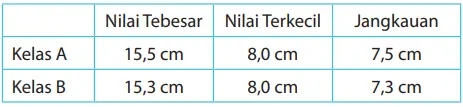
Nilai minimum dari dua kelas adalah sama, namun nilai maksimum dan jangkauan kelas A 0,2 cm lebih panjang.

Penyebaran data seperti di atas disebut distribusi.

Sebaran Data

Deviasi, varians, dan deviasi standar dari data dapat kita hitung dengan rumus berikut.

Deviasi = (nilai numerik dalam data) – (nilai rata-rata)

Varians = {total dari (deviasi kuadrat)} ÷ (jumlah data)

Deviasi standar = akar kuadrat dari varians

Tabel Distribusi Frekuensi

Perhatikan Tabel 2 di halaman 237. Kita kelompokkan nilai-nilai data di Kelas A ke dalam interval-interval yang panjangnya 1 cm, kemudian kita hitung banyaknya siswa pada setiap kelompok seperti yang telah kita lakukan di Sekolah Dasar, sehinggakita peroleh Tabel 3.

Sebuah interval seperti “paling kecil 8 dan kurang dari 9” disebut kelas. Panjang setiap interval disebut interval kelas. Nilai tengah interval kelas disebut nilai kelas. Selanjutnya sebagai contoh, nilai kelas untuk interval kelas “paling kecil 8 dan kurang dari 9” adalah 8,5 cm. Banyaknya data dalam setiap kelas disebut frekuensi kelas.

Tabel 3 menunjukkan penyebaran data menggunakan kelas dan frekuensi, dan disebut sebagai tabel distribusi frekuensi.

Tabel 3 : Data posisi tangkapan penggaris

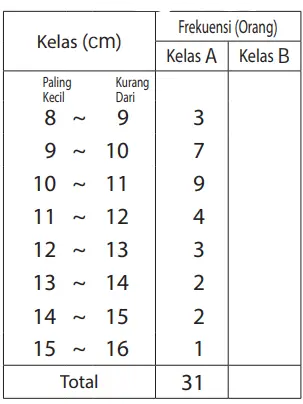
2. Jawablah pertanyaan berikut ini dengan menggunakan Tabel 3.

(1) Berdasarkan Tabel 2 di halaman 237, selidiki frekuensi setiap kelas untuk data siswa Kelas B, kemudian tuliskan pada Tabel 3.

Jawaban:

Dari atas tabel secara berurutan,

7, 6, 2, 4, 5, 4, 2, 1

Total 31

(2) Untuk setiap data Kelas A dan kelas B, kelas manakah yang memiliki frekuensi tertinggi? Berapakah nilainya?

Jawaban:

a. Kelas A

Kelas 10 cm atau lebih dan kurang dari 11 cm
Nilai kelas 10,5 cm

b. Kelas B

Kelas 8 cm atau lebih dan kurang dari 9 cm
Nilai kelas 8,5 cm

(3) Hitunglah banyaknya siswa di setiap kelas yang posisi tangkapannya kurang dari 10 cm.

Jawaban:

a. Kelas A…10 orang,

b. kelas B…13 orang

(4) Apa yang kamu simpulkan ketika membandingkan frekuensi data dua kelas?

Jawaban:

Kesimpulan Perbandingan Data kedua kelas

a. Distribusi di grup B lebih banyak pada kurang dari 10 cm

b. Distribusi di atas 14 cm adalah sama

Pada tabel distribusi frekuensi, nilai kelas yang memiliki frekuensi tertinggi disebut modus. Pada umumnya, ketika menggunakan modus sebagai nilai representatif, maka nilai kelas yang mempunyai frekuensi tertinggi yang digunakan, bukan nilai yang paling sering muncul pada kumpulan data.

Sebagai contoh, berdasarkan Tabel 3, modus data Kelas A adalah 10, 5 cm karena kelas yang memiliki frekuensi tertinggi adalah “paling kecil 10 cm dan kurang dari 11 cm.”

3. Berdasarkan Tabel 3, tentukan modus untuk data Kelas B.

Jawaban:

Karena kelas dengan frekuensi tertinggi adalah lebih dari 8 cm dan kurang dari 9 cm maka nilai modusnya adalah 8,5 cm yang merupakan nilai kelas.

Histogram

Kita dapat menggunakan tabel distribusi frekuensi untuk menggambar grafik dengan persegi panjang yang lebarnya menunjukkan interval kelas, dan tingginya menunjukkan frekuensi. Grafik seperti ini disebut histogram atau diagram batang.

Jika kita menggunakan histogram untuk menyajikan data posisi tangkapan penggaris siswa Kelas A seperti ditunjukkan pada Tabel 3, maka kita peroleh Gambar 1. Jika kita menggunakan tabel distribusi frekuensi untuk menggambar diagram batang, maka data akan mudah kita pahami.

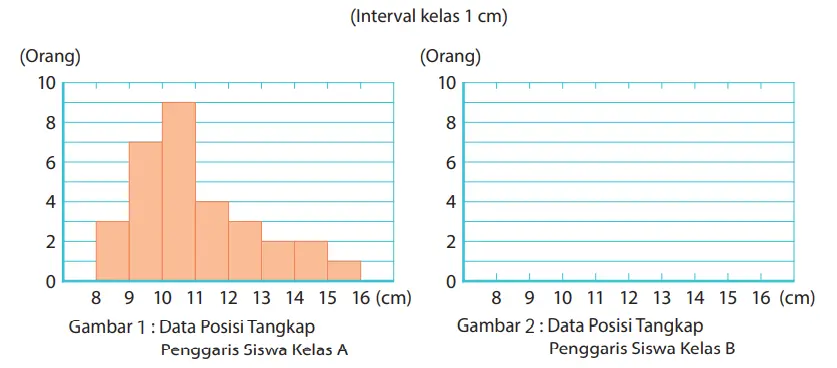
4. Berdasarkan Tabel 3 di halaman 238, gambarlah histogram untuk data “Gambar 2: Data posisi tangkap penggaris siswa Kelas B.

Jawaban:

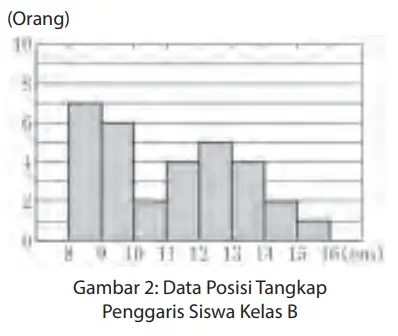
5. Gambar 3 di bawah ini adalah histogram untuk data posisi tangkap penggaris siswa Kelas A dengan interval kelas 2 cm. Gambarlah histogram untuk data posisi tangkap penggaris siswa Kelas B dengan interval kelas 2 cm pada Gambar 4.

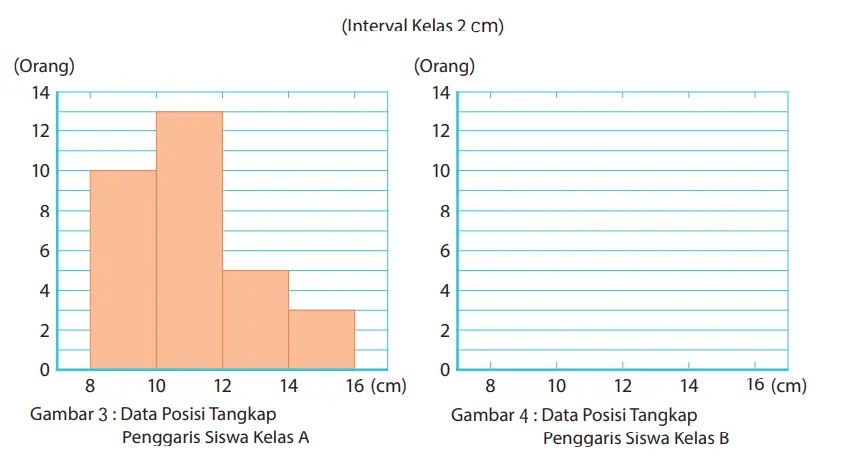
Jawaban:

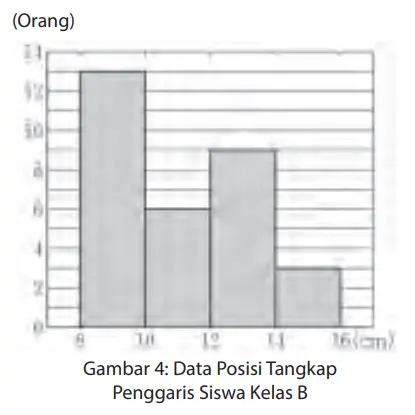
6. Apa perbedaan antara informasi yang dapat kita baca dari histogram di Gambar 1 dan Gambar 3 di halaman sebelumnya? Selanjutnya, bagaimana dengan Gambar 2 dan Gambar 4?

Jawaban:

Dari Gambar 1 terlihat bahwa jumlah orang 10 cm atau lebih dan kurang dari 11 cm adalah 9, yaitu sekitar 30% dari seluruh kelas, tetapi tidak dapat terbaca dari Gambar 3.

Gambar 2 dan Gambar 4 (contoh)

a. Dapat kita lihat dari Gambar 2 bahwa jumlah orang antara 10 cm sampai kurang dari 11 cm adalah kecil dengan hanya 2 orang, tetapi tidak dapat terbaca dari Gambar 4.

b. Dapat kita lihat dari Gambar 2 bahwa jumlah orang antara 8 cm sampai 9 cm adalah yang terbesar, namun tidak dapat terlihat dari Gambar 4.

Meskipun kita menggunakan data yang sama, jika kita gambar histogram dengan interval kelas berbeda, maka sifat data yang dapat kita amati dapat berubah. Ketika menyelidiki distribusi data, maka penting untuk kita perhatikan beberapa histogram dengan interval kelas berbeda.

Pada histogram Gambar 1 pada halaman 239, jika kita ambil nilai tengah di setiap ujung atas empat persegi panjang kemudian kita hubungkan, maka kita peroleh grafik pada Gambar 5.

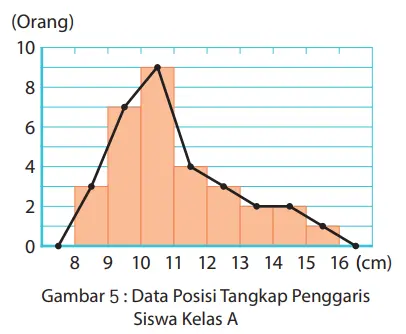
7. Berdasarkan histogram pada Soal 4 di halaman sebelumnya, gambarlah grafik frekuensi garis pada Gambar 2 di halaman sebelumnya. Bandingkanlah Gambar 5 dengan grafik frekuensi garis di Gambar 2 dan diskusikan hasil pengamatanmu.

Jawaban:

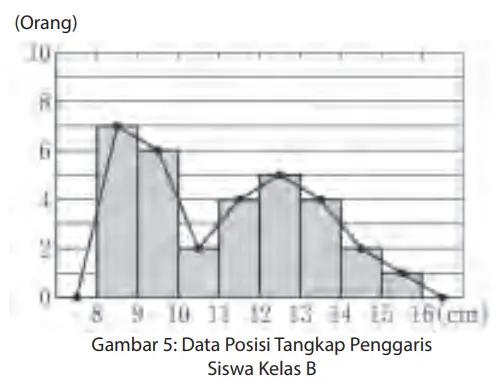
a. Kelas A memiliki satu puncak gunung, Kelas B memiliki dua

b. Pada kelas 10 cm atau lebih dan kurang dari 11 cm, kelompok A memiliki frekuensi paling tinggi, tetapi kelompok B memiliki frekuensi paling rendah.

8. Gambar 6 menunjukkan suhu maksimum harian di Tokyo pada bulan Agustus 1963 dan 2013. Bandingkanlah dua grafik tersebut dan diskusikan apa yang dapat kamu baca dan simpulkan dari grafik-grafik tersebut.

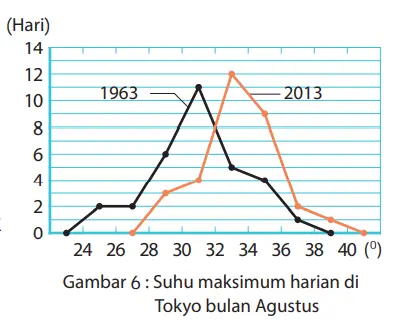
Jawaban:

Karena grafik tahun 2013 bergeser ke kanan secara keseluruhan dibandingkan grafik tahun 1963, terlihat bahwa suhu tahun 2013 secara umum lebih tinggi dibandingkan tahun 1963.

 

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Selanjutnya jangan lewatkan dan dapatkan Berita berita Update lainnya.***