ohgreat.id-Jawaban Ayo Berkomunikasi halaman 155 Penyajian Relasi Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 155. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 4 Relasi dan Fungsi. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Relasi dan Fungsi
- 1.0.1 Diketahui ada dua himpunan bilangan, yaitu bilangan A = {bilangan bulat antara 2 dan 7} dan B = {enam bilangan cacah pertama}. Apabila relasi dari himpunan A ke himpunan B adalah “satu lebihnya dari”, maka coba tentukan daerah domain, kodomain, dan rangenya.
- 1.0.2 Diketahui himpunan A = {2, 3, 4, 5, 6, 7}, dan himpunan B = {4, 9, 16, 25, 36, 49}; relasi antara anggota himpunan A dan B adalah akar dari. Hubungan ini dapat dinyatakan dalam pasangan berurutan, seperti (2,4), yang menunjukkan dua faktor dari empat; (3,9), yang berarti tiga hasil akar dari sembilan; dan seterusnya. Jadi, himpunan relasi dari pasangan terurut adalah {(2,4); (3,9); (5,25); (6,36); (7,49)}. Cobalah temukan untuk membuat setidaknya tiga contoh lebih lanjut dari hubungan antara anggota himpunan A dan B, coba temukan 3 macam relasi lain yang berbeda dari A dan B. Hubungan tersebut kemudian dapat ditunjukkan dengan menggunakan cara diagram panah, koordinat Cartesius, dan himpunan pasangan berurutan.
- 1.0.3 Durahman mengatakan bahwa diagram pada Gambar 4.7 termasuk bukan relasi, karena ada satu anggota yang bukan merupakan anggota dari himpunan B dipasangkan dengan anggota himpunan A, yaitu bilangan 5 dipasangkan dengan huruf f. Akan tetapi, hubungan dari himpunan A ke himpunan B merupakan relasi”. Sedangkan Bahrudin mengatakan bahwa “diagram pada Gambar 4.7 termasuk relasi, meskipun ada satu anggota yang bukan merupakan anggota dari himpunan B dipasangkan dengan anggota himpunan A, yaitu bilangan 5 dipasangkan dengan huruf f. Akan tetapi, hubungan dari himpunan A ke himpunan B bukan merupakan relasi”. Bu Muhas menyimak terhadap kedua pendapat tersebut dan memberikan tanggapan bahwa pernyataan yang tepat adalah pendapat Pak Durahman. Apakah kalian setuju dengan tanggapan Bu Muhas? Coba jelaskan alasan kalian.
Relasi dan Fungsi
Penyajian Relasi
Ayo Berkomunikasi
Diketahui ada dua himpunan bilangan, yaitu bilangan A = {bilangan bulat antara 2 dan 7} dan B = {enam bilangan cacah pertama}. Apabila relasi dari himpunan A ke himpunan B adalah “satu lebihnya dari”, maka coba tentukan daerah domain, kodomain, dan rangenya.
Jawaban Siswa A
Diketahui A = {bilangan bulat antara 2 dan 7}
B = {enam bilangan cacah pertama}
Lalu, mendaftar anggotanya dari kedua bilangan tersebut, yaitu:
A = {3, 4, 5, 6} dan B = {0, 1, 2, 3, 4, 5}
Kemudian, untuk menentukan domain, kodomian, dan range dengan diagram panah
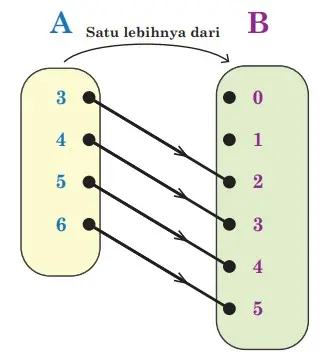
Berdasarkan diagram panah tersebut, didapat daerah ketiganya adalah
Domain = {3, 4, 5, 6}
Kodomain = {0, 1, 2, 3, 4, 5}
Range = {2, 3, 4, 5}
Jawaban Siswa B
Mendaftar anggotanya dari kedua bilangan tersebut, yaitu:
A = {3, 4, 5, 6} dan B = {0, 1, 2, 3, 4, 5}
Untuk menentukan domain, kodomain, dan range dengan diagram Cartesius

Dengan demikian, didapat
Domain = {3, 4, 5, 6}
Kodomain = {0, 1, 2, 3, 4, 5}
Range = {2, 3, 4, 5}
Jawaban Siswa C
Mendaftar anggotanya dari kedua bilangan tersebut, yaitu:
A = {3, 4, 5, 6} dan B = {0, 1, 2, 3, 4, 5}
Relasi dari himpunan A ke himpunan B adalah “satu lebihnya dari”, maka himpunan pasangan berurutannya adalah {(3, 2), (4, 3), (5, 4),(6, 5)}
Oleh karena itu, maka daerah domain, kodomain, dan rangenya didapat:
Domain = {3, 4, 5, 6}
Kodomain = {0, 1, 2, 3, 4, 5}
Range = {2, 3, 4, 5}
Ayo Berpikir Kreatif
Berikut Alternatif Jawaban “Ayo Berpikir Kreatif” yang Bernilai Benar
Relasi yang mungkin dari himpunan P ke Q, dintaranya sebagai berikut:
a. Relasinya “setengah dari”, yakni {(2,4)}
b. Relasinya “faktor dari”, yakni {(2,4); (2,16); (2,36); (3,9); (3,36); (4,4); (4, 16); (4,36); (5,25); (6,36); (7,49)}
c. Relasinya “kurang dari”, yakni {(2,4); (2, 9); ……; (7,49)}
Ayo Berpikir Kritis
Perhatikan Gambar 4.7 pada halaman berikut.
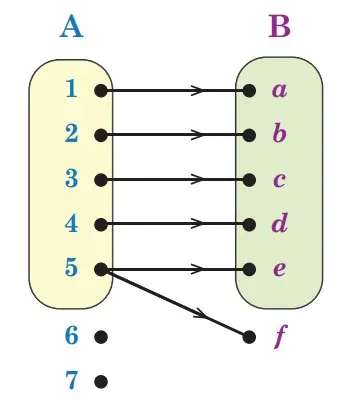
Durahman mengatakan bahwa diagram pada Gambar 4.7 termasuk bukan relasi, karena ada satu anggota yang bukan merupakan anggota dari himpunan B dipasangkan dengan anggota himpunan A, yaitu bilangan 5 dipasangkan dengan huruf f. Akan tetapi, hubungan dari himpunan A ke himpunan B merupakan relasi”. Sedangkan Bahrudin mengatakan bahwa “diagram pada Gambar 4.7 termasuk relasi, meskipun ada satu anggota yang bukan merupakan anggota dari himpunan B dipasangkan dengan anggota himpunan A, yaitu bilangan 5 dipasangkan dengan huruf f. Akan tetapi, hubungan dari himpunan A ke himpunan B bukan merupakan relasi”. Bu Muhas menyimak terhadap kedua pendapat tersebut dan memberikan tanggapan bahwa pernyataan yang tepat adalah pendapat Pak Durahman. Apakah kalian setuju dengan tanggapan Bu Muhas? Coba jelaskan alasan kalian.
Berikut Alternatif Jawaban “Ayo Berpikir Kritis” yang Bernilai Benar
Dikarenakan angka 5 dipasangkan dengan huruf f pada Gambar 4.3, anggota himpunan A yang bukan anggota himpunan B, maka diagram tersebut tidak merepresentasikan suatu relasi. Namun, ada hubungan antara himpunan A dan B tetap disebut sebagai relasi.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
