ohgreat.id-Jawaban Eksplorasi Matematika halaman 212 Sudut Segi Banyak Bintang Beraturan Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 212. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Matematika Lanjut. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Eksplorasi Matematika

Sudut Segi Banyak Bintang Beraturan

Pada gambar di sebelah kanan diberikan 5 titik pada keliling lingkaran yang ditempatkan berjarak sama satu sama lain. Dengan menghubungkan titik-titik dari titik permulaan ke titik kedua (satu titik dilewat), kemudian dihubungkan lagi ke titik lain (melewati satu titik pula) dalam arah yang sama hingga kembali ke titik semula, maka gambar yang terbentuk dinamakan segi banyak bintang beraturan.

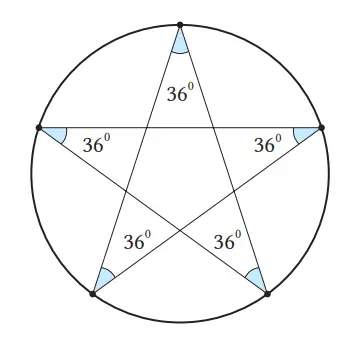
Seperti yang telah kita selidiki di halaman 137, jumlah sudut-sudut dalam dari segi-5 bintang adalah 180°. Sehingga, satu titik sudut pada segi-5 bintang beraturan besarnya adalah 36°.

1. Gambar di sebelah kanan terbentuk dengan cara menghubungkan titik ke-3 pada keliling lingkaran yang telah dibagi menjadi 7 bagian. Carilah jumlah sudut-sudut dalam dari semua titik sudut segi banyak bintang tersebut, lalu tentukan besar sudut untuk tiap titik sudutnya.

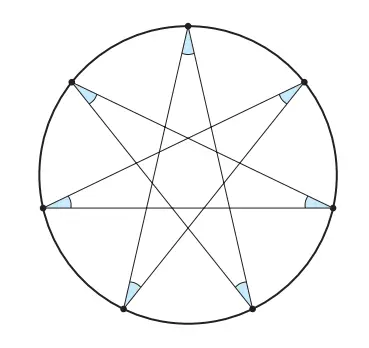
Jawaban:

Jumlah total 7 sudut ujung adalah 180°

Contoh cara mencari jumlah total 7 sudut:

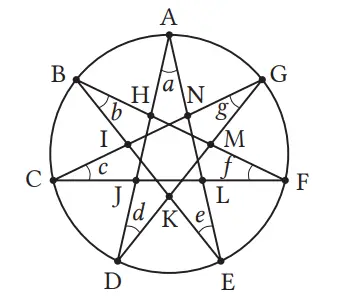
∠b + ∠e + ∠f = ∠ELF = ∠ALJ
∠g + ∠c + ∠d = ∠CJD = ∠AJL

maka dari itu

∠a + ∠b + ∠c + ∠d + ∠e + ∠f + ∠g
= ∠a + ∠ALJ + ∠AJL
= 180°

2. Pada gambar di sebelah kanan, kita hubungkan setiap titik ke-2. Hitunglah jumlah semua sudut dalam dari segi banyak bintang tersebut, dan tentukan pula ukuran untuk tiap sudutnya.

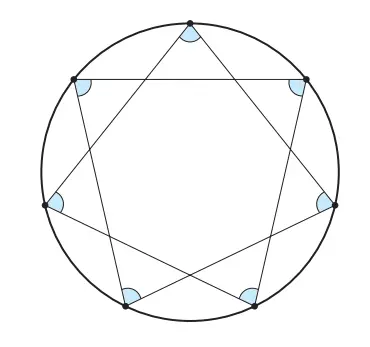
Jawaban:

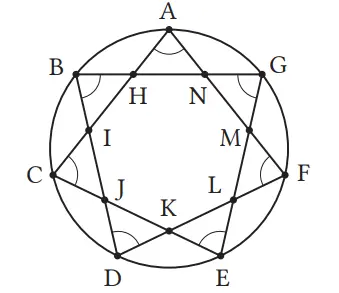
Jumlah total sudut dalam segitiga adalah 180° × 7 = 1.260°.

Karena jumlah total sudut luar bagian dalam segi-7 HIJKLMN adalah 360°, maka jumlah total 7 sudut bagian ujung adalah

1.260° – 360° × 2 = 540°.

Gambar 1 dan 2 bernamakan segi-7 bintang beraturan. Jika kita coba kemungkinan lainnya, kamu hanya akan temukan dua buah segi-7 bintang beraturan.

Penjelasan dan Hal yang Perlu Kita perhatikan

Segi Tujuh Bintang

Ada 1 jenis segi-5 bintang, tapi dapat kita katakan ada 2 jenis segi-7 bintang. Bangun datar (1) terbentuk dengan menghubungkan setiap 4 titik. Bangun datar (2) terbentuk dengan menghubungkan setiap 5 titik. Hal ini wajar mengingat 7 – 3 = 4 dan 7 – 2 = 5, tetapi saya ingin peserta didik menggambar diagram untuk memastikannya.

Selanjutnya, mari kita selidiki bangun yang terbentuk dengan membagi lingkaran ke dalam 8 dan 9 bagian.

3. Gambar di sebelah kanan menunjukkan sebuah keliling lingkaran yang telah dibagi ke dalam 8 bagian. Tanpa menghubungkan 2 titik berdekatan, bagaimana seharusnya kita hubungkan titik-titik agar kita kembali ke titik permulaan? Cari pula jumlah sudut-sudut dalam dari ke-8 titik sudut pada segi banyak bintang yang terbentuk.

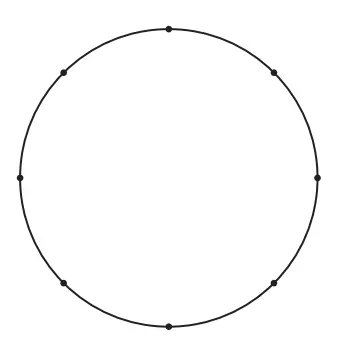
Jawaban:

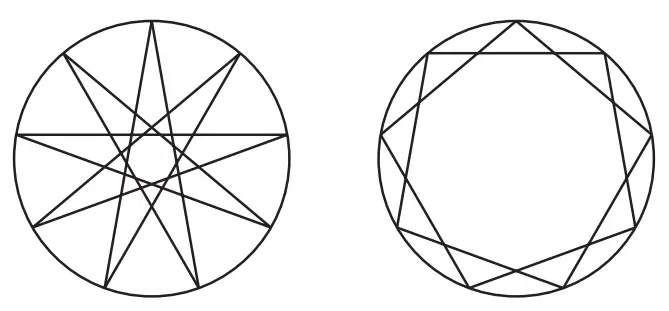
Jika setiap 3 titik kita hubungkan, maka kita bisa menggambar bangun datar berikut.

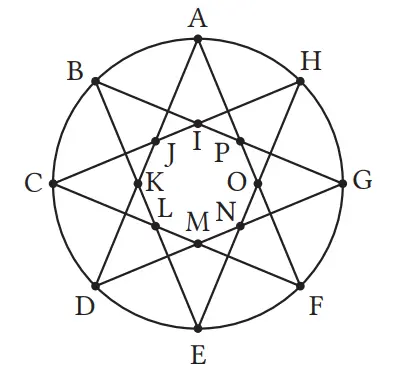
Jumlah total 8 sudut ujung 360°

Besar 1 sudut 45°

(Cara mencari jumlah total 8 sudut)

Pada gambar di atas, dari jumlah total sudut dalam 4 belah ketupat, yaitu AKEO, BLFP, CMGI, dan DNHJ. Memperoleh jumlah total sudut dalam pada segi delapan IJKLMNOP,

360° × 4 – 180o × (8 – 2)
= 360°

※ Menggunakan sifat perbandingan sudut keliling lingkaran dan panjang busur (yang kita pelajari dalam 3 tahun), peserta didik mampu mencari besar 1 sudut pada segi banyak bintang beraturan, dengan menggunakan metode sama untuk semua jenisnya.

(Contoh)

Jumlah sudut di ujung merupakan kelipatan integral dari 180°.

Untuk segi lima bintang dan segi tujuh bintang beraturan, terdapat bangun datar yang jumlah sudut ujungnya 180°.

4. Pada gambar berikut, keliling lingkaran telah dibagi ke dalam 9 bagian. Buatlah gambar bangunnya dan carilah jumlah semua sudut dalam dari ke-9 titik sudut pada segi banyak bintang yang terbentuk (serupa pertanyaan 3 ).

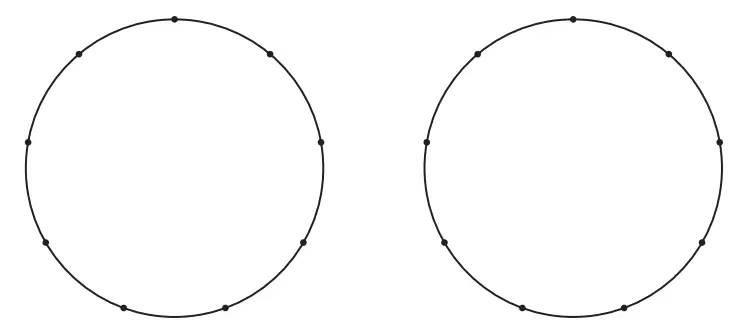
Jawaban:

Jika setiap 4 titik atau 2 titik kita hubungkan, maka setiap bangun datar dapat kita gambar seperti ini.

① Setiap 4 titik

② Setiap 2 titik

① Jumlah total 9 sudut ujung 180°
Besar 1 sudut 20°

② Jumlah total 9 sudut ujung 900°
Besar 1 sudut 100°

Gambar yang dibuat pada 3 dan 4 berturut-turut kita namakan segi-8 bintang beraturan dan segi-9 bintang beraturan. Mulai dari segi-5 bintang beraturan hingga segi-7 bintang beraturan, kesemuanya kita namakan segi banyak bintang beraturan.

Perlu kita pikirkan dengan syarat seperti apa kita bisa menggambar segi banyak bintang. Selain itu, perlu kita perhatikan, bahwa pada bagian dalam segi-n bintang beraturan dapat kita buat segi-n beraturan. Dengan kata lain, dapat kita anggap bahwa bangun datar bintang segi-n beraturan dapat diperoleh dengan menggabungkan segi-n beraturan yang sisinya diperpanjang.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***