ohgreat.id-Jawaban Soal Perkalian halaman 36 Perkalian dan Pembagian Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 36. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 1 Bilangan Bulat. Selanjutnya pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Perkalian dan Pembagian

Perkalian

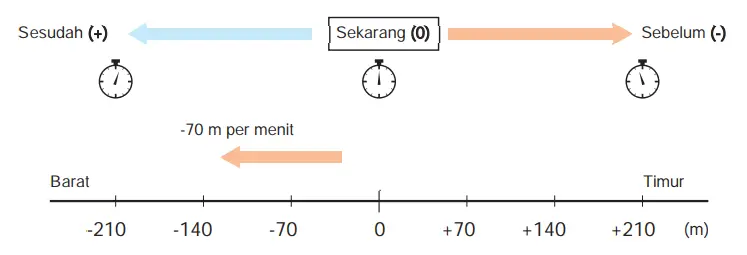
Q. Munir berjalan ke arah timur dengan kecepatan 70 m per menit. Titik awal ditetapkan sebagai 0 m. Arah ke timur sebagai arah positif. Melewati satu menit dihitung sebagai +1 menit.

(1) Di titik manakah Munir setelah berjalan satu menit? Setelah dua menit?

Di titik manakah dia semenit sebelumnya? Dua menit sebelumnya? Selanjutnya tandai (dengan anak panah) lokasi Munir menggunakan diagram berikut ini.

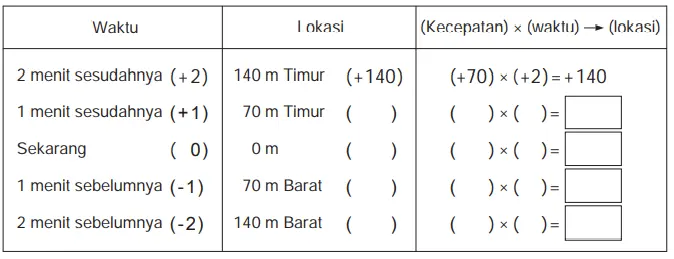
(2) Nyatakanlah lokasi Munir pada saat-saat yang ditentukan dengan mengisi ( ) dan < > dengan angka yang tepat.

Jawaban:

(1) 

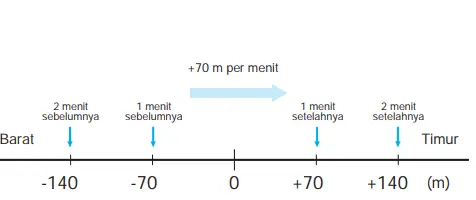
(2) Dari keterangan di atas, diperoleh bahwa

Titik jarak +70, 0 , -70, -140

Rumus/persamaan (+70) × (+1) = +70
(+70) × 0 = 0 ; (+70) × (-1) = -70 ; (+70) × (-2) = –140

1. Berdasarkan , di titik-titik manakah Munir 5 menit sesudahnya dan 10 menit sebelumnya? Selanjutnya nyatakanlah lokasinya dengan kalimat matematika.

Jawaban:

5 menit setelahnya (+70) × (+5) = +350
350 m ke timur

10 menit sebelumnya (+70) × (-10) = -700
700 m ke barat

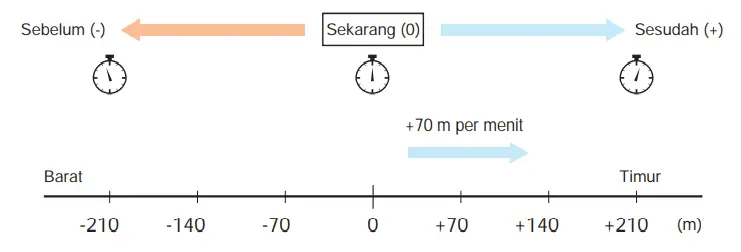
Q. Toni berjalan ke arah barat dengan kecepatan 70 m per menit. Posisi Toni sekarang ditetapkan sebagai titik 0, ke arah ke timur sebagai arah positif, ke barat negatif, melalui selama satu menit sebagai +1 menit.

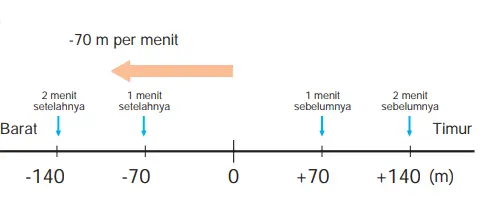
(1) Di titik manakah Toni setelah 1 menit? Setelah 2 menit? Pada titik mana Toni semenit sebelumnya? Dua menit sebelumnya? Selanjutnya tandai lokasinya (dengan anak panah) pada diagram di bawah ini.

(2) Nyatakanlah lokasi Toni pada saat-saat yang ditentukan dengan mengisi ( ) dan < > dengan angka yang tepat.

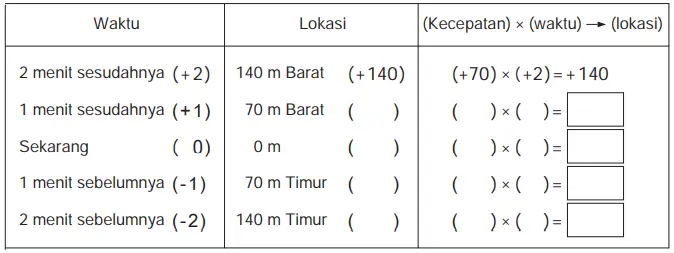
Jawaban:

(1) 

(2) Dari gambar di atas, diperoleh bahwa

Jarak -70, 0 , +70, +140
Persamaan (-70) × (+1) = -70
(-70) × 0 = 0 ; (-70) × (-1) = +70 ;  (-70) × (-2) = +140

2. Berdasarkan , di titik-titik manakah Toni 5 menit sesudahnya dan 10 menit sebelumnya? Nyatakanlah lokasinya dengan kalimat matematika.

Jawaban:

5 menit kemudian (+70) × (+5) = -350
350 m ke barat

10 menit sebelumnya (-70) × (-10) = +700
700 m ke timur

Operasi mengalikan bilangan positif dan negatif juga disebut perkalian.

3. Pada contoh di Q di halaman sebelumnya dan Q di atas, bagaimanakah perubahan hasil kali dengan mengubah besaran waktu? Selanjutnya bandingkan dan diskusikan perbedaannya.

Jawaban:

Siswa harus mengetahui karakteristik berikut dan mendiskusikannya.

(Dalam kasus Q pada halaman 36) *Hasil bertambah sebesar 70. Pengali berubah dari negatif ke positif pada batas 0.

(Dalam kasus Q di halaman 37) Hasil berkurang 70. * pengali berubah dari positif ke negatif pada batas 0.

Perkalian dengan Menggunakan Tanda Positif, Negatif, dan Nilai Mutlak

Dalam mengalikan bilangan positif dan negatif, bagaimana hubungan antara nilai mutlak hasil kali dengan nilai mutlak bilangan-bilangan yang dikalikan? Selanjutnya diskusikan pada Q di halaman 36 dan Q pada halaman sebelumnya.

Jawaban:

Anda harus dapat menjelaskan karakteristik berikut dengan cara Anda sendiri dan selanjutnya siswa dapat menemukannya dalam kerja sama.

1. Perkalian dua bilangan bertanda sama menghasilkan bilangan positif

2. Perkalian dua bilangan dengan tanda yang berbeda menghasilkan bilangan negatif

4. Hitunglah.

(1) (+6) × (+5)              (2) (-7) × (-8)

(3) (+12) × (-3)             (4) (-2) × (+10)

Jawaban:

(1) (+6) × (+5) = +30        (2) (-7) × (-8) = +56

(3) (+12) × (-3) = -36        (4) (-2) × (+10) = -20

Perkalian bilangan positif dengan negatif dapat dirangkum sebagai berikut.

Perkalian Bilangan Positif dan Negatif

1. Hasil kali bilangan dengan tanda sama

Tanda: positif
Nilai mutlak: hasil kali nilai-nilai mutlak dua bilangan yang dikalikan

2. Hasil kali bilangan dengan tanda berbeda

Tanda: negatif
Nilai mutlak: hasil kali nilai mutlak dua bilangan yang dikalikan

5. Tentukan hasil kali +14 dengan +1. Kalikan -6 dengan +1. Selanjutnya tentukan hasil +14 dengan -1, dan -6 dengan -1.

Jawaban:

(+14) × (+1) = +14 (+14) × (-1) = -14

(+6) × (+1) = -6 (-6) × (-1) = +6

Berapapun bilangannya, jika dikalikan dengan 1 hasilnya sama dengan bilangan tersebut. Hasil kali -1 dengan bilangan menghasilkan negatif bilangan tersebut.

6. Berapa hasilnya -8 dikalikan 0, dan jika 0 dikalikan +2?

Jawaban:

(-8) × 0 = 0

0 × (+2) = 0

Berapapun bilangannya, jika dikalikan 0 hasilnya 0.

Contohnya, (8) × 0 = 0 ; 0 × (-2) = 0.

7. Hitunglah.

(1) (+0,5) x (-2)                          (2) (-3,6) × (-1,4)

(3) (-2/3) x (-9)                          (4) （-4/7） × （+7/8）

Jawaban:

(1) (+0,5) x (-2) = -1                       (2) (-3,6) × (-1,4) = +5,04

(3) (-2/3) x (-9) = +6                     (4) （-4/7） × （+7/8） = -1/2

8. Hitunglah.

(1) (+4) × (+2)

(2) (-4) × (-8)

(3) (-7) × (+9)

(4) (+3) × (-10)

(5) (-18) × (-3)

(6) 0 × (-5)

(7) (-4,8) × (+1,3)

(8) （+2/3 ）×（-9/2 ）

(9) （-2,5）×（-4/3）

Jawaban:

(1) (+4) × (+2) = +8

(2) (-4) × (-8) = +32

(3) (-7) × (+9) = -63

(4) (+3) × (-10) = -30

(5) (-18) × (-3) = +54

(6) 0 × (-5) = 0

(7) (-4,8) × (+1,3) = -6,24

(8) （+2/3 ）×（-9/2 ） = -3

(9) （-2,5）×（-4/3） = +10/3

Pertanyaan Serupa

Kerjakan soal berikut

(1) (+9) × (+4)                            (2) (+6) × (-7)

(3) (-5) × (+10)                          (4) (-13) × (-2)

(5) (+2/5) x (-15)                       (6) (-3/4) x (7/12)

Jawaban:

(1) +36              (4) +26

(2) -42               (5) -6

(3) -50               (6) +7/16

 

Sifat Komutatif dan Asosiatif Perkalian

Q. Hitunglah. Selanjutnya bandingkan hasilnya antara a dan b .

(1) a. (+4) × (-3)

b. (-3) × (+4)

(2) a. {(+2) × (-4)} × (-5)

b. (+2) × {(-4) × (-5)}

Jawaban:

1) A, B sama-sama menghasilkan -12

2) A, B sama-sama menghasilkan +40

Sifat-sifat berikut ini berlaku pada perkalian bilangan positif dan negatif.

Sifat komutatif perkalian
a × b = b × a

Sifat asosiatif perkalian
(a × b) × c = a × (b × c)

9. Diskusi

Yuli menghitung sebagai berikut. (-4) × (+9) × (-25) seperti ditunjukkan hitungan ke samping. Jelaskan proses di balik hitungan 1 dan 2 .

Jawaban:

1) Tukar -4 dan +9 menggunakan hukum Komutatif perkalian

2) kerjakan (-4) × (-25) terlebih dahulu menggunakan hukum Asosiatif perkalian

10. Hitunglah

(1) (-50) × (+17) × (-2)                      (2) (+9) × (-4,5) × (+2)

(3) （-1/8) × (+3,6) × (-8)                (4) （+1/3）× (-10) × (-3/5）

Jawaban:

(1) Persamaan = (-50) × (-2) × (+17)
= (+100) × (+17) = +1700

(2) Persamaan = (+9) × {(-4.5) × (+2)}
= (+9) × (-9) = -81

(3) Persamaan = （-1/8) × (-8) x (+3,6)
= (+1) x (+3,6) = +3.6

(4) Persamaan = （+1/3）× <(-10) × (-3/5）>
= (+1/3) x (+6) = +2

Q.Diskusi

Hitunglah, amati, Selanjutnya diskusikan bagaimana tanda dari hasil kalinya.

(1) (+5) × (-2)

(2) (+5) × (-2) × (-3)

(3) (+5) × (-2) × (-3) × (-1)

Jawaban:

(1) (+5) × (-2) = -10

(2) (+5) × (-2) × (-3) = +30

(3) (+5) × (-2) × (-3) × (-1) = -30

Anda harus dapat menjelaskan karakteristik dengan cara Anda sendiri agar siswa dapat menemukannya dalam kerja sama. Tanda hasil perkalian berubah seiring bertambahnya jumlah bilangan negatif. Selanjutnya jika hanya ada 1 bilangan negatif maka tandanya “-”, jika terdapat 2 bilangan negatif tandanya jadi “+”, jika terdapat 3 bilangan negatif tandanya jadi “-” begitu seterusnya.

Berapa kalipun bilangan dikalikan dengan bilangan positif, maka tanda hasil kalinya tidak berubah. Namun, setiap kali kita mengalikan dengan bilangan negatif, maka tanda dari hasil kalinya berubah. Dengan perkataan lain, tanda dari hasil kalinya ditentukan oleh berapa kali dikalikan dengan bilangan negatif.

11. Hitunglah.

(1) (-5) × (-6) × (+2)

(2) (-7) × (-3/14) × (-3/4)

Jawaban:

(1) (-5) × (-6) × (+2) = +60

(2) (-7) × (-3/14) × (-3/4) = -2

Perkalian beberapa bilangan dapat dirangkum sebagai berikut.

Tanda dan Nilai Mutlak Hasil Kali

1) Ketika bilangan negatif muncul sebanyak genap kali, maka tanda hasil kalinya adalah +. Ketika bilangan negatif muncul sebanyak ganjil kali, maka tanda hasil kalinya -.

2) Nilai mutlak hasil kali sama dengan hasil perkalian nilai-nilai mutlak bilangan-bilangan yang dikalikan.

12. Hitunglah.

(1) 4 × (-2) × 6

(2) -5 × 2 × (-7)

(3) (-3,5) × (-2) × 9

(4) -1/3 × 6 × (-4) × (-9)

(5) 8 × (-3) × 1/6 × (-1/4）

(6) (-5) × (-5) × (-5)

Jawaban:

(1) 4 × (-2) × 6 = -48

(2) -5 × 2 × (-7) = 70

(3) (-3,5) × (-2) × 9 = 63

(4) -1/3 × 6 × (-4) × (-9) = -72

(5) 8 × (-3) × 1/6 × (-1/4） = 1

(6) (-5) × (-5) × (-5) = -125

Perpangkatan (Eksponen)

Sebuah bilangan yang dikalikan dengan dirinya beberapa kali Soal 12 6 di halaman sebelumnya merupakan bilangan yang dinyatakan dalam bentuk eksponen.5 × 5 dituliskan sebagai 5², dan dibaca “5 pangkat dua atau 5 kuadrat” 5 × 5 × 5 dituliskan sebagai 5³, dan disebut “lima pangkat tiga”.

Angka kecil yang muncul di atas angka yang pertama menunjukkan berapa kali bilangan dipangkatkan. Bilangan pangkat tersebut dinamakan eksponen.

13. Nyatakan perkalian berikut dalam bentuk perpangkatan eksponen.

(1) 2 × 2 × 2

(2) (-4) × (-4)

(3) （-3/5) × (-3/5)

Jawaban:

(1) 2³

(2) (-4)²

(3) (-3/4)²

14. Nyatakan luas persegi dengan panjang sisi 5 cm, kemudian hitung volume kubus dengan panjang sisi 5 cm.  Selanjutnya nyatakan dalam bentuk eksponen. Satuan apa yang paling cocok digunakan?

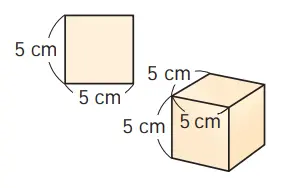
Jawaban:

Luas Persegi = s x s
= 5 x 5 = 5² = 25

Volume Kubus = s x s x s
= 5 x 5 x 5 = 5³ = 125

Berkaitan dengan satuan luas dan volume dari kubus dan persegi (cm² dan cm³), hal ini dapat digunakan sebagai salah satu contoh penerapan bentuk eksponen atau perpangkatan. Selanjutnya Area dan volume spesifik dibahas di hal.14. Juga, perhatikan bahwa ketika persamaan dalam bentuk pangkat dimasukkan, adalah umum untuk keliru antara 5³ dengan 5 × 3.

15. Hitunglah.

(1) (-10)²                   (2) -10²            (3)（-4/7)²

(4) 0,3²                      (5) (-2)³            (6) -2³

Jawaban:

(1) 100                      (4) 0.09

(2) -100                     (5) -8

(3) 16/49                  (6) -8

 

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Selanjutnya jangan lewatkan dan dapatkan Berita berita Update lainnya.***