ohgreat.id-Pengertian Korespondensi Satu-satu halaman 190 Korespondensi Satu-satu (Pengayaan) Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 190. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 4 Relasi dan Fungsi. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Relasi dan Fungsi

Korespondensi Satu-satu (Pengayaan)

Pengertian Korespondensi Satu-satu

Perhatikan dengan cermat pada Gambar 4.11 di bawah, untuk memahami konsep korespondensi satu-satu, lihatlah deretan rumah di area tertentu atau dekat dengan rumah kalian. Setiap rumah dibedakan dari yang lain dengan nomor rumah yang unik. Apakah mungkin untuk memiliki dua nomor rumah di satu perumahan? Apakah juga ada kemungkinan dua rumah berbagi nomor rumah yang sama? Secara alami, jawabannya adalah tidak. Korespondensi satu-satu merupakan fungsi khusus yang menghubungkan rumah dengan nomornya.

Gambar 4.11 deretan rumah

Ayo Bereksplorasi

Ada lima siswa telah memiliki nomor induk sekolah di SMP Semangat 45, kelima siswa tersebut tentunya memiliki nomor induk khusus buat nomor induk masing-masing yang tidak akan dimiliki oleh siswa lain, yakni seperti berikut.

1. Nomor induk Ahmad adalah 219,

2. Nomor induk As’ari adalah 279,

3. Nomor induk Tohir adalah 292,

4. Nomor induk Tauiq adalah 258,

5. Nomor induk Wati adalah 224,

Apabila A dinyatakan mewakili himpunan siswa, maka anggotaanggota himpunan A adalah {Ahmad, As’ari, Tohir, Tauiq, Wati} dan anggota-anggota himpunan B adalah {219, 224, 258, 279, 292}, sehingga “nomor induk” merupakan relasi yang mungkin dari himpunan A ke himpunan B, dan “nama pemilik nomor induk” merupakan relasi yang mugkin dari himpunan B ke himpunan A, maka sajian diagram panah pada Gambar 4.12 merupakan relasi dari kedua himpunan tersebut. Perhatikan secara khusus uraian berikut untuk menemukan dua diagram panah pada kasus tersebut.

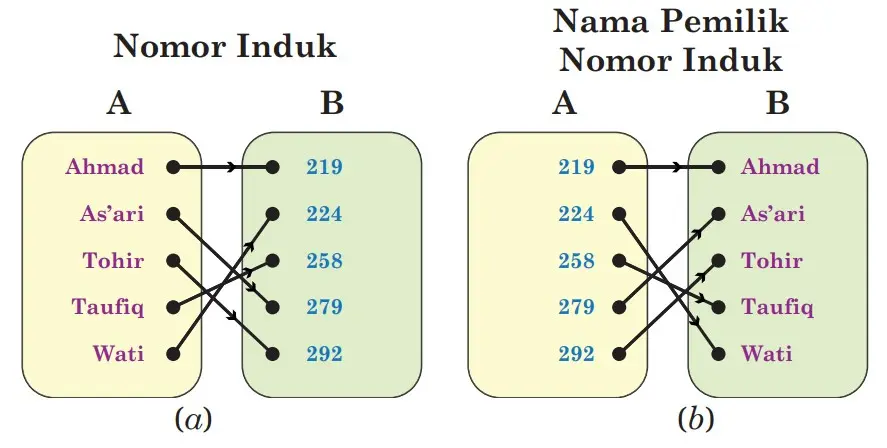
Gambar 4.12 diagram panah

Berdasarkan Gambar 4.12a menunjukkan bahwa setiap elemen A memiliki satu pasangan dengan setiap anggota B. Sehingga, “nomor induk” merupakan relasi dari himpunan A ke B yang dapat disebut juga sebagai fungsi (pemetaan). Semua elemen himpunan B dapat disebut sebagai pemetaan (bayangan) dari elemen himpunan A dan dipasangkan dengan tepat satu oleh anggota himpunan A. Sedangkan yang terjadi pada Gambar 4.12b merupakan kebalikannya. Pemetaan dua arah seperti yang ditunjukkan pada Gambar. 4.12 dapat juga disebut sebagai fungsi satu-satu.

Perhatikan dengan cermat relasi dari anggota himpunan A ke B yang digambarkan pada Tabel 4.2 di bawah ini.

Tabel 4.2 contoh korespondensi satu-satu dan contoh bukan korespondensi satu-satu

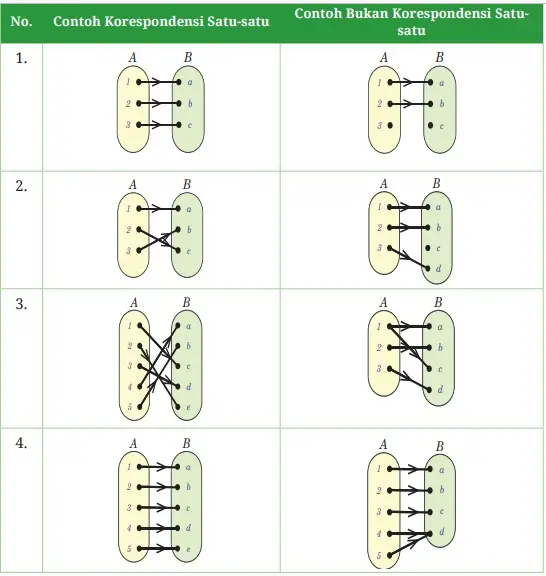
Pengertian:

Korespondensi satu-satu adalah fungsi khusus yang memasangkan tepat satu untuk setiap anggota daerah asal maupun daerah kawan. Dengan kata lain, dapat dikatakan bahwa setiap anggota dari daerah asal maupun dari daerah kawan hanya mempunyai satu pasang.

Contoh 4.12

Apabila diketahui himpunan-himpunan berikut, maka tentukan yang termasuk korespondensi satu-satu. Jelaskan.

1. Himpunan P = {1, 2, 3, 4} dan himpunan Q = {a, b, c, d}

2. Himpunan R = {x, y, z} dan himpunan S = {5, 6}

Alternatif penyelesaian

1. Diketahui anggota himpunan P adalah {1, 2, 3, 4} dan anggota himpunan Q adalah {a, b, c, d}, sehingga banyak anggota keduanya dapat ditulis n(P) = 3 dan n(Q) = 3.

Jadi, banyak anggota keduanya sama, sehingga dapat dinotasikan dengan n(P) = n(Q). Dengan demikian, himpunan P dan himpunan Q merupakan korespondensi satu-satu.

2. Diketahui himpunan R = {x, y, z} dan himpunan S = {5, 6}, sehingga banyak anggota keduanya dapat ditulis n(R) = 3 dan n(S) = 2

Jadi, banyak anggota keduanya tidak sama, sehingga n(R) ≠ n(S). Dengan demikian, himpunan R dan S bukan merupakan korespondensi satu-satu.

Ayo Berpikir Kritis

Menurut Sulastri, perbedaan antara relasi, fungsi, dan korespondensi satu-satu adalah setiap relasi tidak selalu dapat disebut sabagai fungsi dan korespondensi satu-satu, setiap relasi tidak selalu dapat disebut sebagai korespondensi satu-satu tetapi pasti dapat disebut sebagai relasi, dan setiap korespondensi satu-satu pasti selalu dapat disebut sebagai relasi dan fungsi. Sedangkan Rudi tidak setuju dengan pendapat Sulastri, karena Rudi punya pendapat lain tentang perbedaan antara relasi, fungsi, dan korespondensi satu-satu; yaitu korespondensi satusatu dapat disebut sebagai himpunan bagian dari fungsi dan relasi, begitu juga fungsi dapat disebur sebagai himpunan bagian dari relasi. Setujukah kalian dengan pendapat Rudi? Jelaskan. Ataukah kalian justru setuju dengan pendapat Sulastri? Jelaskan.

Berikut Alternatif Jawaban Ayo Berpikir Kritis yang Bernilai Benar.

Setiap relasi tidak selalu merupakan fungsi dan korespondensi satu-satu, setiap relasi tidak selalu merupakan korespondensi satu-satu tetapi pasti suatu relasi, dan setiap korespondensi satu-satu pasti selalu relasi dan fungsi.

Ayo Berpikir Kreatif

Diketahui himpunan K = {1, 2, 3, 4} dan himpunan L = {a, b, c, d}. Muhasshanah menemukan hubungan kedua himpunan tersebut yang dapat dikatakan sebagai korespondensi satu-satu, yaitu {(1, a); (2, b); (3, c); (4, d)}. Sedangkan Mukhsin menemukan hubungan kedua himpunan tersebut yang dapat dikatakan sebagai korespondensi satu-satu, yaitu {(1, b); (2, a); (3, d); (4, c)}. Kalau kalian, dapatkah kalian menemukan bentuk susunan himpunan pasangan berurutan yang berbeda? Temukan sebanyak mungkin susunan himpunan pasangan berurutan berbeda-beda.

Berikut Alternatif Kegiatan Ayo Berpikir Kreatif.

Coba kalian kedua bentuk korespondensi satu-satu yang ditemukan oleh Muhasshanah dan Mukhsin. Jika ada temanmu yang kurang mengerti, karena jawaban kurang lengkap. Coba apa yang perlu ditambahkan dalam dalam penyelesaian tersebut agar lebih lengkap dan jelas sehingga temanmu lebih mengerti.

Siswa diharapkan memahami masalah dengan beberapa korespondensi satu-satu dalam tugas ini. Memberikan kesempatan kepada siswa untuk memahami sebelum memberikan kesempatan kepada mereka untuk menyampaikan atau menjelaskan kepada siswa lain apa yang telah mereka pahami.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***