ohgreat.id-Pengertian Kemiringan halaman 223 Persamaan Garis Lurus Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 223. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 5 Persamaan Garis Lurus. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Persamaan Garis Lurus
Pengertian Kemiringan
Ayo Bereksplorasi
Gambar 5.8 Tangga bersandar pada dinding
Perhatikan secara khusus tangga yang disandarkan pada dinding samping rumah pada Gambar 5.7. Tangga yang disandarkan ke dinding merupakan gambaran bagaimana garis lurus digunakan dalam kehidupan sehari-hari. Kemiringan tangga yang tepat harus diperhitungkan agar aman, nyaman, dan tidak berbahaya untuk dinaiki. Dapatkah kalian menentukan nilai kemiringan tangga tersebut? Dapatkah nilai kemiringan dipandang sebagai gradien dalam persamaan garis lurus?
Sekarang, cobalah untuk menemukan sesuatu dalam kehidupan sehari-hari yang menyerupai Gambar 5.8, yang menunjukkan kemiringan suatu garis.
Definisi
Kemiringan adalah rasio antara jarak vertikal terhadap jarak horizontal. Persamaan berikut menyatakan pengertian Kemiringan.
Kemiringan = perubahan panjang sisi tegak vertikal : perubahan panjang sisi mendatar horizontal
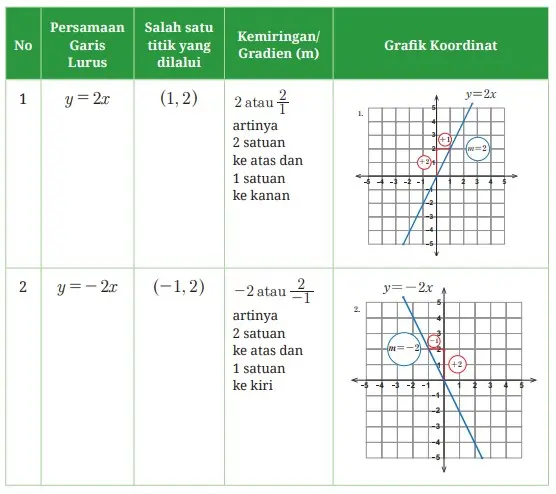
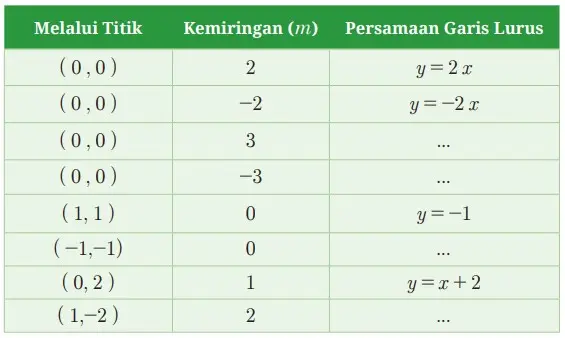
Sekarang, coba perhatikan baik-baik sajian Tabel 5.1 agar kalian dapat memahami kemiringan suatu garis dengan mudah. Setelah itu, coba lengkapi Tabel 5.1 di bawah ini.
Tabel 5.1 Kemiringan Persamaan Garis Lurus yang Melalui Dua Titik Koordinat
Berdasarkan hasil kegiatan pada kedua persamaan di atas, coba kalian eksplorasikan hasil diskusinya dengan menjawab beberapa pertanyaan berikut.
1. Apa yang membedakan garis yang melalui pusat koordinat dengan garis yang melalui titik lain dalam sistem koordinat?
2. Pada koordinat Cartesius, mengapa beberapa garis miring ke kanan sementara yang lain miring ke kiri?
3. Bagaimana cara menentukan persamaan garis dengan kemiringan m yang melalui pusat koordinat?
4. Bagaimana persamaan garis yang melalui sembarang titik (x1,y1) dan bergradien m?
Contoh 5.3
Jika diketahui garis dengan kemiringan 3 yang melalui titik A(2,5); maka tentukan persamaan garis tersebut.
Alternatif penyelesaian
titik A(2,5), maka x1 = 2 dan y1 = 5 dan m = 3.
Persamaan garisnya adalah y – y1 = m(x – x1)
⇔ y – 5 = 3 (x – 2)
y – 5 = 3x – 6
⇔ y = 3x – 6 + 5
y = 3x – 2
Jadi, persamaan garis dengan kemiringan 3 yang melalui titik A(2,5) adalah y = 3x – 2
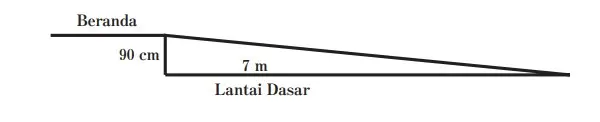
Sekarang pikirkan tentang masalah berikutnya. Gambar 5.9 di bawah ini mengilustrasikan teras belakang sekolah. Hal ini akan dibuat lebih sederhana bagi pengguna kursi roda dengan pembangunan jalur baru. Jika panjang jalan yang akan dibuat 7 meter dari tepi beranda, apakah memenuhi syarat keselamatan bagi pengguna kursi roda?
Gambar 5.9 serambi belakang sekolah
Berapa panjang jalan terkecil yang dapat dibuat agar dapat diakses oleh pengguna kursi roda?
Perhatikan dengan cermat pada Gambar 5.9 di atas; menunjukkan bahwa beranda naik 90 cm di atas permukaan tanah, dan jalan memanjang 7 m, atau 700 cm, dari bibir beranda. Persamaan berikut dapat digunakan untuk menghitung kemiringan jalan yang akan dibangun.
Kemiringan = perubahan panjang sisi tegak (tinggi beranda) : perubahan panjang sisi mendatar (panjang jalan dari bibir beranda)
= 90 : 700
= 9 : 70 = 0,128
Dengan demikian, karena jalan yang sedang dibangun memiliki kemiringan kurang dari 0,15; maka sudah sesuai dengan peraturan keselamatan pengguna kursi roda.
Tahukah Kalian?
Tahukah kalian bahwa Australia, negeri Kanguru, memiliki aturan dan larangan terkait kemiringan suatu jalan atau lintasan tertentu?
Untuk mengakomodasi pengguna kursi roda, kemiringan jalan tidak boleh melebihi 0,15.
Kemiringan tidak boleh lebih dari 0,25 di area parkir yang aman.
Kemiringan tidak boleh lebih dari 0,875 persen pada anak tangga bangunan.
Untuk pejalan kaki, kemiringan trotoar tidak boleh lebih besar dari 0,325.
Jarak terpendek yang dapat dibangun dengan tetap aman bagi pengguna kursi roda timbul dari kemiringan jalan yang direkomendasikan sebesar 0,15.
Dengan asumsi bahwa untuk jalur terpendek yang diperlukan adalah memiliki panjang x2 maka perhitungannya dapat dilakukan seperti berikut.
Kemiringan = perubahan panjang sisi tegak (tinggi beranda) : perubahan panjang sisi mendatar (panjang jalan terpendek)
0,15 = 90 : x substitusikan ukuran yang diketahui
0,15x = 90 kalikan keda ruas oleh x
x = 600bagi kedua ruas oleh 0,15
Jadi, jalur terpendek dari tepi anak tangga adalah 600 cm, atau 6 meter.
Ayo Mencoba
Agar kalian lebih memahami cara mendapatkan persamaan garis lurus, cobalah berbicara dengan teman kalian tentang pertanyaan berikut:
1. Apa pengetahuan dan pemahaman kalian tentang kemiringan garis lurus?
2. Apa yang dapat kalian simpulkan dari kemiringan garis lurus?
3. Bagaimana cara menemukan persamaan garis lurus jika diketahui kemiringan dan titiknya?
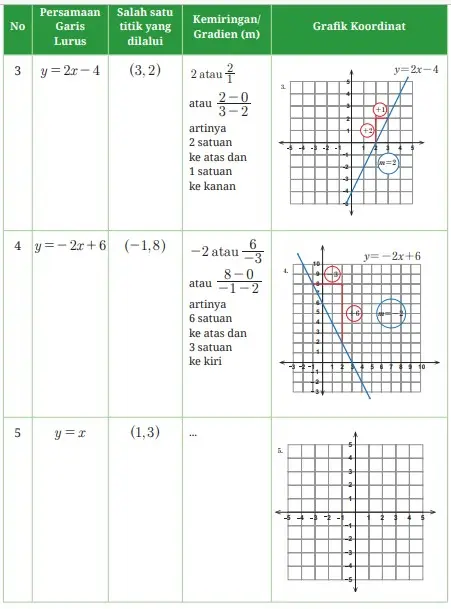
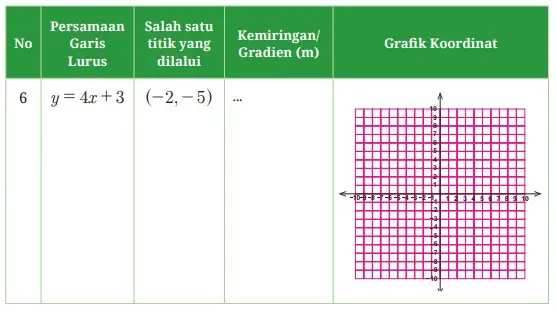
Coba kalian perhatikan dengan cermat Tabel 5.2 berikut, kemudian lengkapi.
Tabel 5.2 Persamaan garis lurus dengan kemiringan dan melalui titik tertentu
4. Jika diketahui kemiringan garis lurus seperti berikut ini, maka gambarlah graiknya.
a. m = -1/2
b. m = – 1
c. m = – 2
d. m = 1/2
e. m = 1
f. m = 2
Perhatikan baik-baik garis yang telah kalian gambar. Berapakah kemiringan garis tersebut?
Coba simpulkan, menurut kalian apa hubungan antara gambar garis lurus dan kemiringan?
Ayo Berpikir Kreatif
Segitiga siku-siku terdiri dari tiga titik: A(a,5),B(-2,3),dan C.(3,b)
Dapatkah kalian menemukan kemungkinan terbentuknya segitiga siku-siku dan ukuran kemiringannya dengan membuat sketsa? Jelaskan alasan kalian.
Ayo Berpikir Kritis
Menurut Durahman, suatu garis tidak mempunyai nilai kemiringan jika sejajar dengan sumbu y dan kemiringannya bernilai nol jika sejajar dengan sumbu x. Burhan, di sisi lain mengatakan bahwa setiap garis sejajar memiliki nilai kemiringan yang sama dan hasil kali dari dua kemiringan garis saling tegak lurus adalah -1. Setujukah kalian dengan pendapat Durahman dan Burhan? Jelaskan alasan kalian.
Petunjuk Guru untuk Kegiatan “Ayo Berikir Kritis”
Lakukan kegiatan alternatif berikut untuk membantu siswa dalam memahami dari kedua pernyataan tersebut:
Kegiatan 1
Agar pengetahuan siswa lebih mendalam terkait kedudukan dua garis atau lebih, cobalah ajak siswa untuk melakukan kegiatan pengamatan berikut:
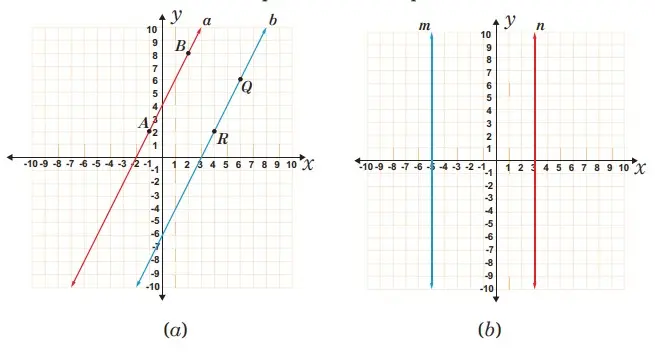
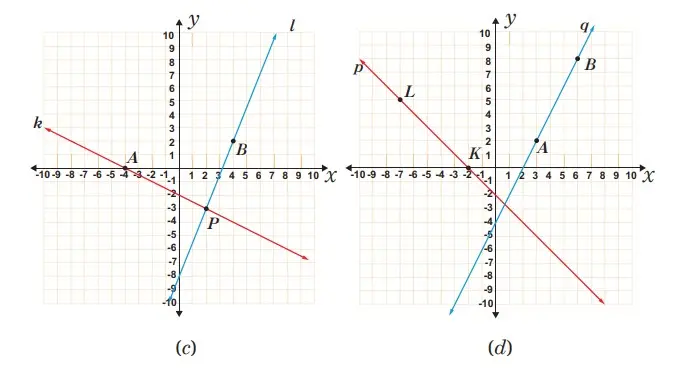
Mintalah siswa untuk memperhatikan keempat Gambar berikut ini
Berdasarkan keempat gambar di atas, ajaklah siswa untuk berdiskusi pertanyaan-pertanyaan berikut dengan kelompoknya.
1. Pertanyaan terhadap gambar (a).
a. Benarkah bahwa garis a dan b adalah dua garis saling sejajar? Coba Jelaskan.
b. Berapakah besar kemiringan dari kedua garis tersebut? Kesimpulan apa yang didapat?
2. Pertanyaan terhadap gambar (b).
a. Benarkah bahwa garis m dan n adalah dua garis saling sejajar? Coba Jelaskan.
b. Berapakah besar kemiringan dari kedua garis tersebut? Kesimpulan apa yang didapat?
3. Pertanyaan terhadap gambar (c).
a. Benarkah bahwa garis k dan l adalah dua garis saling berpotongan saja ataukah saling berpotongan tegak lurus? Jelaskan.
b. Berapakah besar kemiringan dari kedua garis tersebut? Kesimpulan apa yang didapat?
c. Coba kalikan besar kemiringan garis k dan l ? bagaimana hasil kalinya?
4. Pertanyaan terhadap gambar (d).
a. Benarkah bahwa garis p dan q adalah dua garis saling berpotongan? Coba Jelaskan.
b. Berapakah besar kemiringan dari kedua garis tersebut? Kesimpulan apa yang didapat?
c. Coba kalikan besar kemiringan garis p dan q? bagaimana hasil kalinya?
5. Bagaimana dengan besar kemiringan garis a, b, dan c pada gambar (a), apakah sama?
Bagaimana juga dengan besar kemiringan garis m dan n pada gambar (b), apakah sama?
6. Apakah besar kemiringan garis saling berpotongan pada gambar (c) dan (d) memperoleh hasil kali yang sama?
7. Buatlah rumus atau kesimpulan tentang kemiringan garis saling sejajar, garis saling berpotongan dan garis saling tegak lurus.
Kegiatan 2
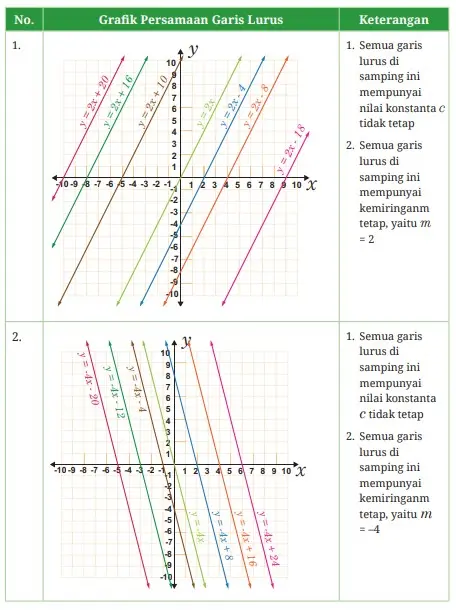
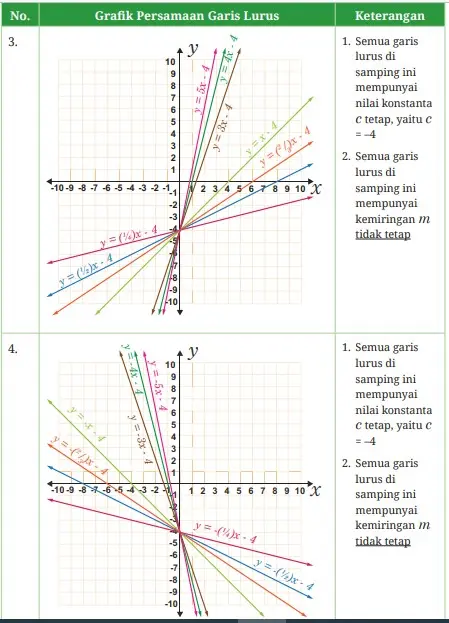
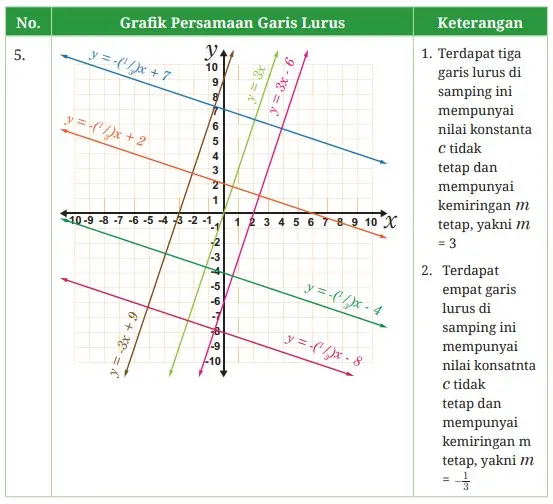
Siswa harus diingatkan terkait dengan bentuk umum persamaan garis lurus, yaitu y = mx + c, hal ini bertujuan untuk memahami karakteristiknya. Siswa akan mempelajari karakteristik persamaan garis lurus dalam latihan pertama ini, baik yang muncul dalam persamaannya maupun sebagai perubahan nilai koeisien atau konstanta tertentu.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***