ohgreat.id-Jawaban Syarat untuk Jajargenjang halaman 153 Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 153. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Segi Empat
Syarat untuk Jajargenjang
Q. Buatlah titik D pada gambar sebelah kanan, dan cobalah buat Jajargenjang ABCD. Mari kita perhatikan cara menentukan posisi titik D dengan berbagai cara, dan coba jelaskan cara menggambarkannya.
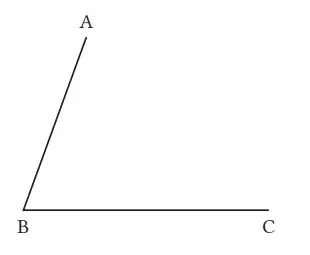
Jawaban:
Selain metode yang ditunjukkan dalam Buku Siswa, metode berikut dapat dipertimbangkan.
(1) Gambarlah AF, suatu garis yang membuat BC // AF, dan ambil titik D dengan BC = AD pada AF.
(2) Hubungkan dua titik A dan C untuk mencari titik tengah O pada ruas garis AC, dan perpanjang ruas garis BO. Ambil titik D di mana BO = DO.
(3) Gambarlah AF, suatu garis yang membuat BC // AF, dan ambil titik D pada AF dengan BA = CD.
(Perhatikan bahwa dalam kondisi ini, titik D dapat digambar dengan dua cara.)
Buat dua sinar CE dan AF yang memenuhi BA // CE dan BC // AF, serta misalkan D titik potong kedua sinar tersebut.
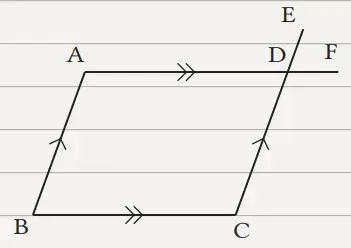
Buat lingkaran dengan pusat C dan BA sebagai jari-jarinya. Selanjutnya Buat juga lingkaran lain dengan A sebagai pusat dan BC sebagai jari-jari. Misalkan D adalah titik potong kedua lingkaran.
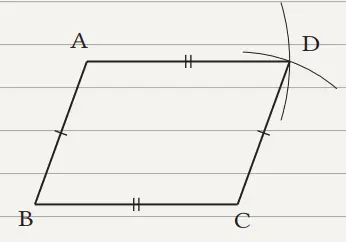
Catatan:
Sinar CE adalah suatu garis yang dibentuk dari titik C sebagai titik pangkal, dan memanjang ke satu arah yang melalui titik E.
Soal 1
Tentukan bagian yang diketahui dan bagian kesimpulan dari pernyataan berikut dengan menggunakan gambar di sebelah kanan. “Segi empat dengan dua pasang sisi berhadapan sama panjang dinamakan jajargenjang.”
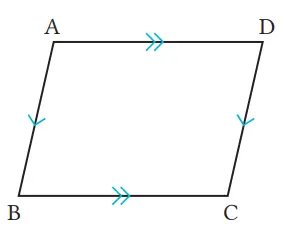
Jawaban:
⟨Asumsi⟩ AB = DC, AD = BC
⟨Kesimpulan⟩ AB//DC, AD//BC
Soal 2
Pada segi empat ABCD, buktikan bahwa jika ∠A = ∠C dan ∠B = ∠D, maka AB // DC dan AD // BC, sesuai urutan (1) , (2) , (3) , (4).
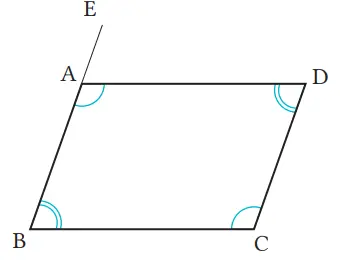
(1) ∠A + ∠B = 180°
Jawaban:
Karena jumlah sudut dalam segi empat adalah 360°,
∠A + ∠B + ∠C + ∠D = 360°
Dari asumsinya,
∠A = ∠C, ∠B = ∠D
Oleh karena itu, ∠A + ∠B = 180°
(2) Jika BA diperpanjang hingga terbentuk BE, maka ∠EAD = ∠B.
Jawaban:
∠BAD + ∠EAD = 180°
Dari ①, ∠BAD + ∠B = 180°
Oleh karena itu, ∠EAD = ∠B
(3) AD // BC
Jawaban:
Dari ②, karena sudutnya sama, AD // BC
(4) AB // DC
Jawaban:
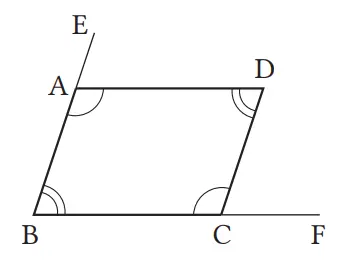
Jika BC diperpanjang ke BF, dengan cara yang sama seperti ① dan ②, ∠B = ∠DCF
Jadi, AB // DC.
Soal 3
Jika kita misalkan O adalah titik potong kedua diagonal segi empat ABCD, buktikan bahwa jika AO = CO dan BO = DO, maka AB//DC dan AD//BC.
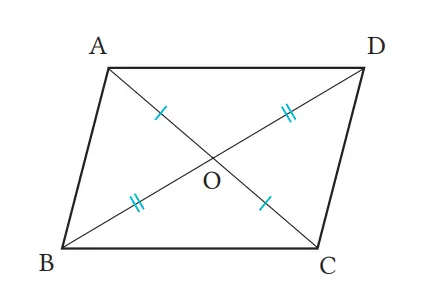
Jawaban:
Dalam ΔABO dan ΔCDO, dari asumsi,
AO = CO ①
BO = DO ②
Karena besar sudut bertolak belakang adalah sama, maka ∠AOB = ∠COD ③
Dari (1), (2), dan (3), dan menurut aturan kekongruenan sisi-sudut-sisi, maka ΔABO ≅ ΔCDO
Oleh karena itu, karena sudut bersesuaian pada ΔABO dan ΔCDO adalah sama, yaitu ∠BAO = ∠DCO, maka AB // DC ④
Demikian pula, ΔAOD ≅ ΔCOB
Oleh karena itu, ∠DAO = ∠BCO maka AD // BC ⑤
Dari ④ dan ⑤, AB // DC, AD // BC.
Soal 4
Pada segi empat ABCD, buktikan bahwa jika AD//BC dan AD = BC, maka segi empat ABCD adalah jajargenjang.
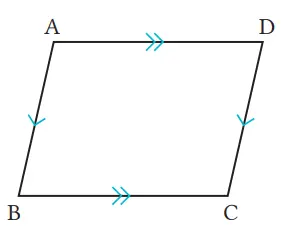
Jawaban:
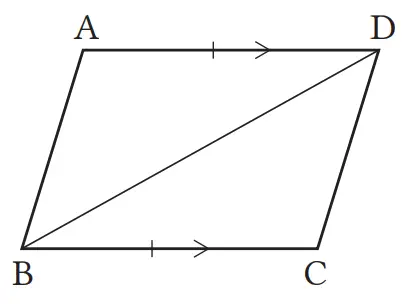
Gambarlah diagonal BD.
Dalam ΔABD dan ΔCDB, dari asumsi, AD = CB ①
Karena sudut dalam berseberangan pada garis sejajar AD//BC adalah sama, maka ∠ADB = ∠CBD ②
BD sisi persekutuan ③
Dari (1), (2), dan (3), dan menurut aturan kekongruenan sisi-sudut-sisi, maka
ΔABD ≅ ΔCDB
Oleh karena itu, karena ∠ABD = ∠CDB maka AB // DC ④
Dari asumsinya, AD // BC ⑤
Dari (4) dan (5), segi empat ABCD adalah jajargenjang.
Soal 5
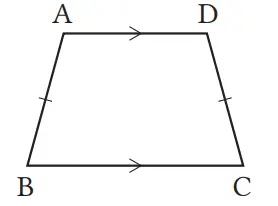
Pada segi empat ABCD, jika AD//BC dan AB = DC, maka dapatkah kita menyatakan bahwa segi empat ABCD adalah jajargenjang?
Jawaban:
Tidak dapat dikatakan jajargenjang.
Hal-hal yang telah kita selidiki sejauh ini dapat dirangkum ke dalam sebuah teorema berikut.
Dengan menggunakan sifat-sifat jajargenjang, mari kita selesaikan beragam permasalahan.
Contoh 2
Pada gambar jajargenjang ABCD di sebelah kanan, jika titik E dan F terletak pada diagonal AC demikian sehingga AE = CF, maka buktikan bahwa segi empat EBFD adalah jajargenjang.
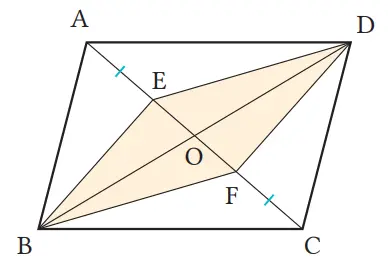
Bukti
Misalkan O adalah titik potong kedua diagonal jajargenjang. Karena perpotongan diagonal-diagonal jajargenjang berada tepat di tengah, maka BO = DO ①
AO = CO ②
Dari soal diketahui bahwa AE = CF ③
Dari ② dan ③, AO – AE = CO – CF
Karena EO = AO – AE , FO = CO – CF, maka EO = FO ④
Dari ① dan ④, karena dua diagonal jajargenjang berpotongan tepat di titik tengahnya, maka segi empat EBFD adalah jajargenjang.
Soal 6
Buktikan pernyataan yang sama di Contoh 2 dengan menggunakan teorema syarat untuk jajargenjang di (2).
Jawaban:
Dari asumsi ΔABE dan ΔCDF, AE = CF ①
Karena sudut dalam berseberangan dari garis sejajar AB // DC, maka ∠BAE = ∠DCF ②
Karena sisi berlawanan dari jajargenjang sama, AB = CD ③
Dari (1), (2), dan (3), menurut aturan kekongruenan sisi-sudut-sisi, maka ΔABE ≅ ΔCDF
Oleh karena itu, BE = DF ④
Demikian pula, ΔAED ≅ ΔCFB
Oleh karena itu, ED = FB ⑤
Dari (4) dan (5), EBFD segi empat adalah jajargenjang karena dua pasang sisi berlawanan adalah sama.
Soal 7
Bila kita misalkan titik M dan N masing-masing merupakan titik tengah AB dan DC dari jajargenjang ABCD, buktikan bahwa segi empat MBND adalah jajargenjang.
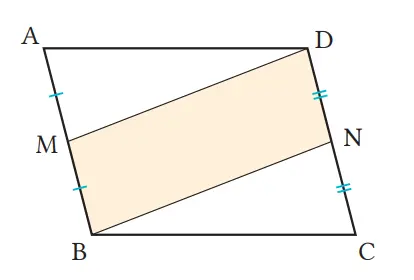
Jawaban:
Karena sisi-sisi yang berlawanan dari jajargenjang adalah sama, maka AB = DC ①
Dari asumsi, didapat MB = 1/2 AB, DN = 1/2 DC ②
Selanjutnya Dari ①, ②, dengan asumsi MB = DN, maka ③MB // DN ④
Dari ③, ④, segi empat MBND adalah jajargenjang karena sepasang sisi yang berhadapan sejajar dan sama besar.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
