ohgreat.id-Jawaban Soal Volume Prisma dan Tabung halaman 221 Volume Bangun Ruang Matematika SMP Kelas 7 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 221. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 6 Bangun Ruang. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
Volume Bangun Ruang
Siswa dapat menghitung volume bangun ruang.
Q. Hitunglah volume prisma segi empat dan tabung berikut ini.
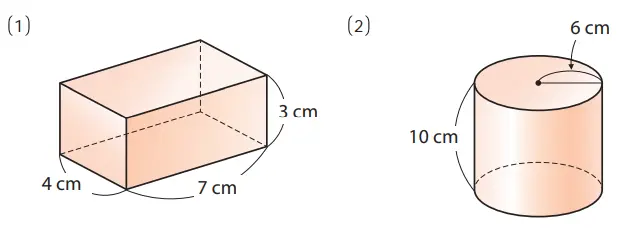
Jawaban:
(1) 4 × 7 × 3 = 84 (cm3)
(2) (π × 62) × 10 = 360π (cm3)
Sebagaimana telah dipelajari di Sekolah Dasar, volume prisma dan tabung adalah (Luas alas) × (Tinggi)
Volume Prisma dan Tabung
Jika luas alas prisma atau tabung adalah L cm2,
tinggi t cm, maka volumenya adalah V cm3,
V = Lt
Catatan t dan V merupakan huruf pertama dari tinggi dan volume.
1. Hitunglah volume bangun ruang berikut ini.
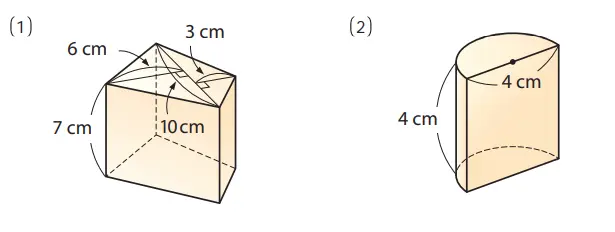
Jawaban:
(1) Jika pertama-tama kita cari luas alas, maka
1/2 × 10 × 6 + 1/2 × 10 × 3 = 84 (cm²)
Karenanya, volumenya adalah 45 × 7 = 315 (cm³)
(2) Jika pertama-tama kita cari luas alas, maka
(π × 22) : 2 = 2π (cm²)
Karenanya, volumenya adalah
2π × 4 = 8π (cm³)
Volume Limas dan Kerucut
Q. Bandingkan volume prisma, limas, tabung, dan kerucut yang mempunyai luas alas dan tinggi yang sama dengan menggunakan wadah.

Jawaban:
Volume air dalam wadah limas atau kerucut dianggap sepertiga dari volume prisma atau tabung, karena terdapat tiga gelas air dalam wadah prisma atau tabung dengan luas alas dan tinggi yang sama.
Berdasarkan hasil di Q, kita dapat melihat bahwa volume limas dan kerucut sama dengan 1/3 volume prisma dan tabung dengan luas alas dan tinggi yang sama.
Volume Limas dan Kerucut
Jika luas alas limas atau kerucut adalah L cm2 , tingginya adalah t cm, maka volumenya adalah V cm3
V= 1/3 Lt
2. Hitunglah volume bangun ruang berikut ini.
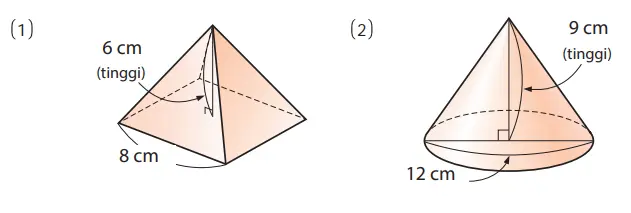
Jawaban:
(1) 1/3 × 82 × 6 = 128 (cm3)
(2) 1/3 ×(π × 62) × 9 = 108π (cm3)
Cermati
Volume Limas Menggunakan Miniatur
1. Marilah kita membuat tiga limas persegi menggunakan jaring-jaring yang disediakan di akhir buku 2 , kemudian bentuklah menjadi sebuah kubus.
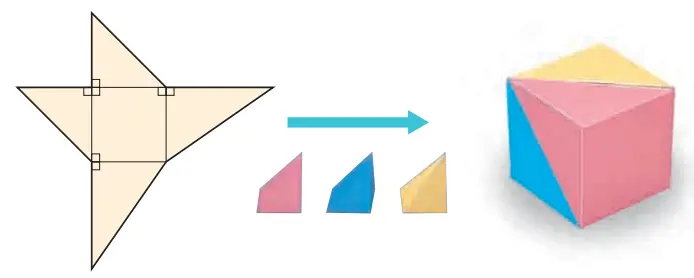
Berdasarkan 1 , kita dapat melihat bahwa volume masing-masing limas persegi sama dengan 1/3 volume kubus. Alas limas menjadi salah satu permukaan kubus.
Jawaban:
Dari [1], model limas segi empat memiliki luas alas dan tinggi yang sama dengan kubus. Volume limas segi empat adalah sepertiga dari volume prisma segi empat yang luas alas dan tingginya sama, karena kubus kita bentuk dengan mengumpulkan ketiganya.
2. Marilah kita membuat enam limas persegi dengan jaring-jaring yang tersedia di akhir buku 2 , kemudian kita susun menjadi kubus.
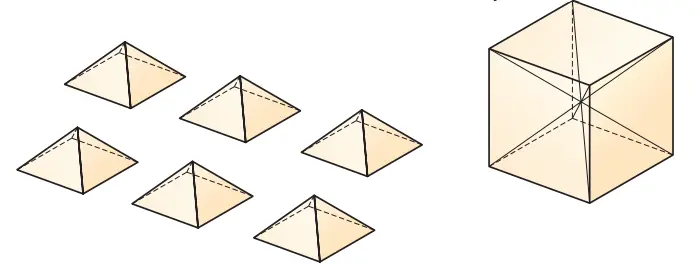
Dari gambar di atas, tampak bahwa volume limas persegi di atas adalah 1/6 volume kubus. Permukaan-permukaan kubus merupakan alas-alas limas, sehingga tinggi kubus sama dengan dua kali tinggi limas.
Jawaban:
Dari [2], model limas segi empat memiliki luas alas yang sama dengan kubus dan tingginya setengah. Volume limas segi empat setengah tingginya adalah 1/6 volume prisma segi empat dengan luas alas dan tinggi yang sama, karena kubus kita bentuk dengan mengumpulkan enam buah. Oleh karena itu, volume limas segi empat adalah 1/3 dari volume prisma segi empat yang luas alas dan tingginya sama satu sama lain.
3. Berdasarkan 1 dan 2 , di atas, jelaskan mengapa volume limas persegi sama dengan 1/3 volume prisma persegi yang mempunyai luas alas dan tinggi yang sama.
Jawaban:
Bangun ruang yang dapat kita bentuk dari jaring-jaring [1] adalah limas miring yang tidak kita bahas dalam teks buku pelajaran, tetapi harus kita pahami secara intuitif bahwa jika posisi puncak digeser, itu menjadi limas persegi biasa volume yang sama.
Juga, di 2, kita dapati bahwa volume limas segi empat beraturan dengan luas alas yang sama dan setengah tingginya dari kubus adalah 1/6 dari volume kubus, sehingga volume limas segi empat adalah 1/3 dari limas segi empat dengan tinggi yang sama. Bisa juga berpikir menggunakan balok dengan tinggi setengah dari kubus sejak awal. Ketika kita potong seperti yang ditunjukkan pada gambar di sebelah kanan,balok menghasilkan empat limas segiempat beraturan yang ada di buku pelajaran, dan empat limas segi empat hasil memotongnya menjadi dua.
Oleh karenanya, volume limas segiempat dapat dijelaskan sebagai 1/3 volume prisma segi empat yang luas alas dan tingginya sama.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
