ohgreat.id-Jawaban Soal Translasi halaman 186 Transformasi Bangun Geometri Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 186. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 5 Bangun Datar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Transformasi Bangun Geometri

Translasi

Contoh 1

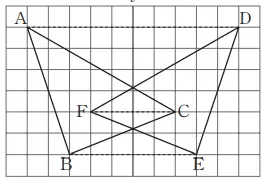
Pada gambar di samping kanan ini, ∆DEF merupakan bangun geometri yang kita hasilkan dari ∆ABC yang digeser searah dan sepanjang anak panah.

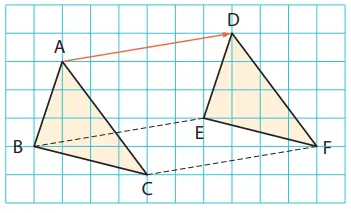
Transformasi dengan menggeser bangun geometri suatu arah tertentu sejauh suatu jarak tertentu banak ang menyebutnya translasi. Dalam AD // BE //CF menyatakan bahwa AD, BE, dan CF saling sejajar.translasi, setiap titik pada bangun geometri kita transformasikan ke arah yang sama sejauh jarak yang sama. Jadi, pada Contoh 1 di atas,

AD // BE //CF, dan AD = BE = CF.

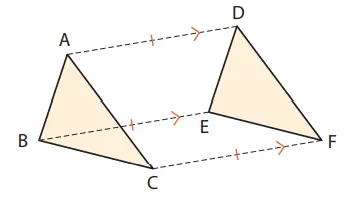
1. Untuk ∆ABC dan ∆DEF pada Contoh 1, jawablah pertanyaan berikut ini.

(1) Apa hubungan antara sisi-sisi yang bersesuaian AB dan DE, BC dan EF, CA dan FD?

Jawaban:

AB//DE, AB = DE

BC//EF, BC = EF

CA//FD, CA, FD

(2) Apa hubungan antara sudut-sudut yang bersesuaian ∠A dan ∠D, ∠B dan ∠E, ∠C dan ∆F?

Jawaban:

∠A = ∠D

∠B = ∠E

∠C = ∠F

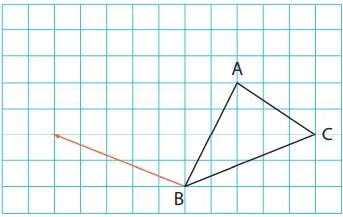
2. Pada gambar di samping kiri, gambarlah ∆DEF yang kita hasilkan dari ∆ABC yang kita translasikan searah dan sejauh anak panah.

Jawaban:

Rotasi

3. Pada gambar bangun di sebelah kanan, jawablah pertanyaan berikut ini.

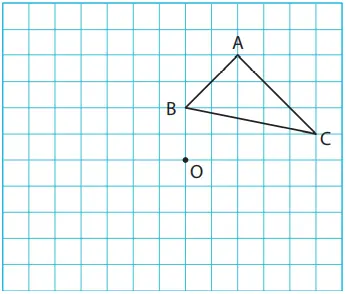
(1) Gambarlah ∆DEF yang dihasilkan dengan memutar ∆ABC sejauh 90° berlawanan arah jarum jam dengan titik O sebagai pusat.

Jawaban:

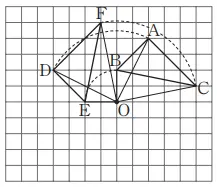
(2) Gambarlah ∆GHI yang dihasilkan dengan memutar ∆ABC secara simetri titik dengan O sebagai pusat.

Jawaban:

Pencerminan

Contoh 3

Pada gambar di samping kanan, ∆ DEF merupakan bangun geometri yang dihasilkan ketika ∆ ABC dibalik menggunakan garis lipat l.

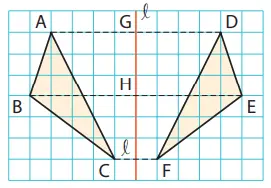
Transformasi yang membalik bangun geometri menggunakan garis disebut pencerminan atau refleksi. Garis lipatan kita sebut sumbu pencerminan.

Pada Contoh 3, ketika bangun geometri Kita cerminkan menggunakan garis l, maka segmen garis AG dan DG sama panjangnya. Akhirnya, l merupakan bisektor tegak lurus dari segmen garis AD.

Jadi, l ⊥ AD dan AG = DG.

4. Pada gambar di Contoh 3, bagaimana garis l berpotongan dengan garis BE dan CE? Selanjutnya nyatakanlah jawabanmu menggunakan simbol-simbol.

Jawaban:

l ⊥ BE , BH = EH

l ⊥ CF, CI = FI

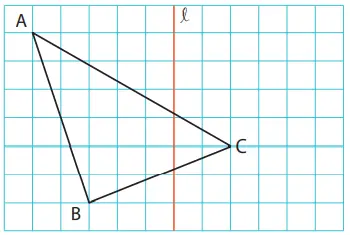
5. Pada gambar di samping kiri, gambarlah ∆DEF merupakan bangun geometri yang dihasilkan ketika ∆ABC kita cerminkan menggunakan garis l sebagai sumbu pencerminan.

Jawaban:

Jika sebuah bangun geometri Kita translasi, Kita rotasi, atau kita cerminkan, maka hasilnya adalah bangun geometri yang sama dan sebangun. Ketika kita menggabungkan beberapa transformasi, maka kita dapat mentransformasikan bangun datar menjadi beberapa posisi.

6. Delapan trapesium sama dan sebangun ditunjukkan pada gambar di samping kanan. Berdasarkan gambar tersebut, jawablah pertanyaan berikut ini.

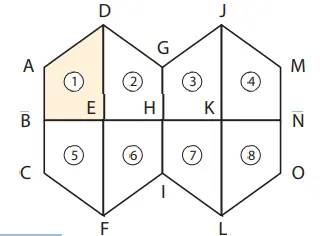
(1) Jika kita pilih titik E sebagai pusat rotasi untuk merotasi (1), Selanjutnya bangun mana yang kita hasilkan?

Jawaban:

⑥

(2) Jika kita menggunakan garis DE sebagai sumbu pencerminan untuk mencerminkan (1), kita lanjutkan dengan menggunakan garis EH sebagai sumbu pencerminan berikutnya, bangun manakah yang dihasilkan?

Jawaban:

⑥

(3) Bagaimana kita mentransformasikan (1) menjadi (8) dengan satu kali gerakan (satu transformasi)?

Jawaban:

Rotasi simetri titik dengan titik H sebagai sumbu rotasinya

(4) Bagaimana mentransformasikan (1) menjadi (8) dalam 2 gerakan (transformasi)? Selanjutnya jawablah dengan dua cara.

Jawaban:

a. Refleksi dengan garis GH sebagai sumbu refleksinya ④, kemudian kita lakukan lagi refleksi dengan garis KN sebagai sumbu refleksinya.

b. Refleksi dengan garis BF sebagai sumbu refleksinya ⑤, kemudian kita lakukan lagi refleksi dengan garis HI sebagai sumbu refleksinya.

c. Rotasi simetri titik dengan titik E sebagai pusat rotasinya ⑥. Selanjutnya translasi ke arah kanan sepanjang HN.

d. Translasi ke arah kanan sepanjang EK ③. Selanjutnya kemudian rotasi simetri titik dengan K sebagai titik pusat rotasinya.

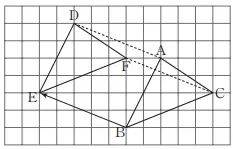
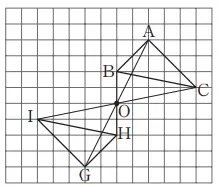
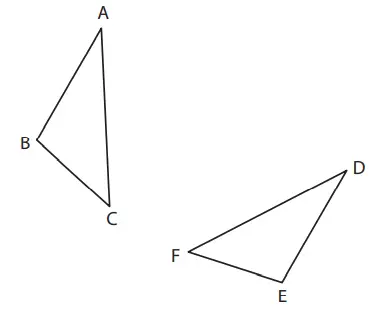
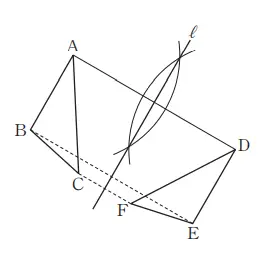
7. Pada gambar di sebelah kanan, ∆DEF merupakan bangun geometri yang dapat kita hasilkan ketika ∆ABC kita cerminkan. Selanjutnya Temukan garis l yang merupakan sumbu simetri.

Jawaban:

Hubungkan 2 titik yang berkorespondensi (titik A dan D, titik B dan C, titik C dan F), kemudian jika kita tarik garis sumbu terhadap segmen garis tersebut, maka ia akan menjadi sumbu sumetri l.

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***