ohgreat.id-Jawaban Soal Ringkasan halaman 23 Menyederhanakan Bentuk Aljabar Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 23. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 1 Menyederhanakan Bentuk Aljabar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Soal Ringkasan

Gagasan Utama

1. Jawablah setiap pertanyaan berikut menggunakan a sampai f.

a) 4x + 7

b) 2x²

c) 3x – 5y

d) -8x

e) 6xy + 9y

f) x² – 6x +1

(1) Manakah yang merupakan bentuk-bentuk suku tunggal?

Jawaban:

(b) 2x², (d) -8x

(2) Manakah yang merupakan bentuk-bentuk linear?

Jawaban:

(a) 4x + 7, (c) 3x – 5y, (e) 6xy + 9y

2. Sederhanakanlah.

(1) 8a2 + 6a + a2 – 2a

(2) -2x – 8y + 7y – 3x + 5

(3) (4a – 9b) + (3a + 5b)

(4) (5x + 2y) – (6x – 4y)

Jawaban:

(1) 8a² + 6a + a² – 2a = 9a² + 4a

(2) -2x – 8y + 7y – 3x + 5 = –5x – y + 5

(3) (4a – 9b) + (3a + 5b) = 7a – 4b

(4) (5x + 2y) – (6x – 4y) = –x + 6y

3. Sederhanakanlah.

(1) (20x – 4y) : (–4)

(2) (5a – 8b) + 3(–a + 2b)

(3) 5 (x + 3y) – 4(2x – y)

(4) (3x + y)/4 – (x – y)/6

(5) 7x × 4y

(6) 3a² × (–2a)

(7) (–9x)²

(8) (–16a²) : 4a

(9) 6xy : 3/7x

(10) 4x² : 6x² × 3x

Jawaban:

(1) 20x – 4y) : (–4) = -5x + y

(2) (5a – 8b) + 3(–a + 2b) = 2a – 2b

(3) 5 (x + 3y) – 4(2x – y) = –3x + 19y

(4) (3x + y)/4 – (x – y)/6 = (7x + 5y)/12

(5) 7x × 4y = 28xy

(6) 3a² × (–2a) = -6a3

(7) (–9x)² = 81x²

(8) (–16a²) : 4a = –4a

(9) 6xy : 3/7x = 14y

(10) 4x²: 6x² × 3x = 2x

4. Perbaiki kesalahan pada perhitungan berikut dan tuliskan jawaban yang benar.

(1) 18xy : 3x × 2y

= 18xy : 6xy = 3

(2) 6ab : [(-2/3)a]

= 6ab x [(-3/2)a] = -9a²b

Jawaban:

(1) 18xy : 3x × 2y = 18xy × 1/3x × 2y

= (18xy x 2y)/3x = 12y²

(2) 6ab : [(-2/3)a] = 6ab x -3/2a

= -9b

5. Jika x = 6 dan y = –5, tentukan nilai-nilai untuk setiap bentuk aljabar berikut.

(1) 14xy² : 7y

(2) (3x + 5y) – (x + 6y)

Jawaban:

(1) 14xy² : 7y

= 14 (6) (-5) 2 : 7(-5)

= -60

(2) (3x + 5y) – (x + 6y)

= (3(6) + 5(-5)) – (6 + 6(-5))

= 17

6. Jelaskan dengan menggunakan bentuk aljabar: mengapa jumlah 3 bilangan bulat dengan selisih 3, seperti 1, 4, 7 adalah kelipatan 3.

Jawaban:

Dari 3 buah bilangan bulat dengan selisih 3, jika bilangan bulat terkecilnya adalah n, maka 3 buah bilangan bulat yang berselisih 3 adalah n, n + 3, n + 6.

Jumlah dari ketiganya adalah

n + (n + 3) + (n + 6)

= 3n + 9

= 3(n + 3)

n + 3 adalah bilangan bulat, maka 3(n + 3) adalah kelipatan 3.

Jadi, jumlah 3 buah bilangan bulat yang selisihnya 3 adalah kelipatan 3.

7. Selesaikan setiap persamaan berikut untuk variabel dalam [ ].

(1) 3x + 2y = 10 [y]

(2) a = (4b + 3c)/7 [c]

Jawaban:

(1) 3x + 2y = 10 [y]

y = (10 -3x)/2 [y = 5- 3/2x]

(2) a = (4b + 3c)/7 [c]

c = (7a – 4b)/3

Penerapan

1. Sederhanakanlah

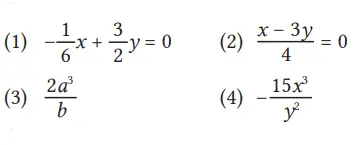
Jawaban:

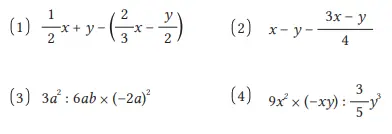
2. Jika kita misalkan A = x2 – 3x – 5 dan B = –2×2 + x + 7, bentuk aljabar apa yang harus dikurangkan dari A untuk menghasilkan B?

Jawaban:

Rumus pencariannya adalah C, maka

A – C = B

Sehingga,

C = A – B

= (x2 – 3x – 5) – (–2×2 + x + 7)

= x2 – 3x – 5 + 2×2 – x – 7 = 3×2 – 4x – 12

Jawaban: 3×2 – 4x – 12

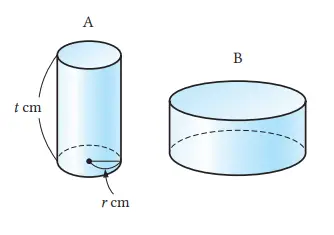
3. Tabung A memiliki jari-jari alas r cm dan tinggi t cm. Tabung B memiliki jari-jari alas dua kali panjang jari-jari alas tabung A, dan tingginya 1/2 dari tinggi tabung A. Gunakan bentuk-bentuk aljabar untuk menjelaskan berapa kali ukuran volume

tabung B terhadap tabung A.

Jawaban:

Volume tabung A adalah πr²h cm³

Di lain pihak, volume tabung B adalah

π × (2r)² × ½h = 2πr²h (cm³)

Jadi, volume tabung B adalah 2 kali volume tabung A.

4. Pada kalender di sebelah kanan, jumlah 3 buah bilangan 2, 9, dan 16 ditandai dengan lingkaran merah sama dengan 3 kali bilangan yang di tengah, yaitu 9. Dapatkah kita menyatakan hal yang sama tentang jumlah 3 bilangan berurutan secara vertikal di tempat lain pada kalender tersebut? Jelaskan jawabanmu dengan menggunakan bentuk-bentuk aljabar.

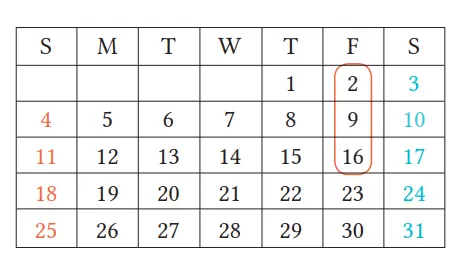
Jawaban:

Dari 3 buah bilangan yang berderet vertikal di kalender, jika bilangan di tengah adalah n, maka 3 buah bilangan yang berderet vertikal adalah

n – 7, n, n + 7. Jumlah ketiganya adalah (n – 7) + n + (n + 7) = 3n

n adalah bilangan tengah, maka 3n adalah 3 kali lipat bilangan tengah.

Jadi, jumlah 3 buah bilangan yang berderet di kalender adalah 3 kali lipat bilangan tengahnya.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***