ohgreat.id-Jawaban Soal Ringkasan halaman 132 Bab 4 Menyelidiki Sifat-Sifat Bangun Geometri Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 132. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 4 Menyelidiki Sifat-Sifat Bangun Geometri. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Soal Ringkasan
- 1.1 Penggunaan Praktis
- 1.1.1 Metode Thales
- 1.1.2 1. Jawablah pertanyaan-pertanyaan berikut.
- 1.1.2.1 (1) Pada Metode Thales, dengan menggunakan gambar di kanan, ia menemukan jarak A ke kapal dengan menggunakan AB = DE. Buktikan bahwa AB = DE.
- 1.1.2.2 (2) Pada Metode Thales, ia memisalkan ∠BAC dan ∠EDC sebesar 90°. Bagian (a) , (b) , (c) , dan (d) berikut merupakan pernyataan-pernyataan terkait ∠BAC dan ∠EDC. Pilih pernyataanpernyataan yang benar.
- 1.1.3 Penjelasan dan Hal yang Perlu Diperhatikan
- 1.1 Penggunaan Praktis
Soal Ringkasan
Penggunaan Praktis
Thales, matematikawan Yunani Kuno abad 6 SM, telah menemukan cara menentukan jarak antara suatu daratan dan sebuah kapal laut yang tak dapat diukur secara langsung.
Metode Thales
(1) Lihatlah kapal B dari A.
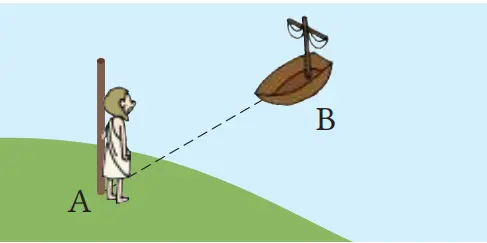
(2) Pada titik A, berputarlah 90°, kemudian tentukan sembarang jarak dan berjalanlah ke arah tersebut lalu tempatkan tongkat di C. Lanjutkan berjalan ke depan dengan arah dan jarak yang sama hingga D.
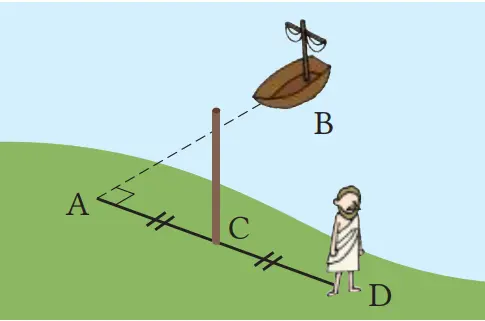
(3) Pada D, lihat ke arah C, dan berputar 90° ke arah berlawanan B. Berjalanlah ke depan pada arah tersebut, dan namai titik untuk melihat tongkat C dan kapal B yang segaris dengan titik E.
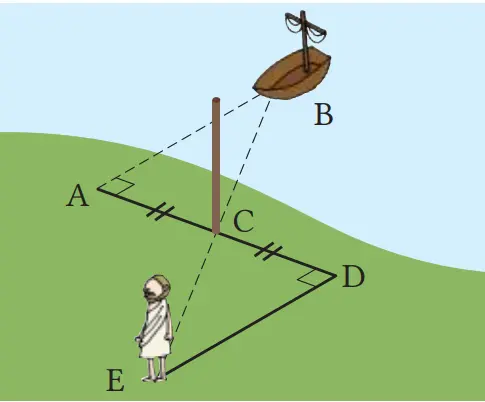
(4) Ukurlah jarak D dan E.
1. Jawablah pertanyaan-pertanyaan berikut.
(1) Pada Metode Thales, dengan menggunakan gambar di kanan, ia menemukan jarak A ke kapal dengan menggunakan AB = DE. Buktikan bahwa AB = DE.
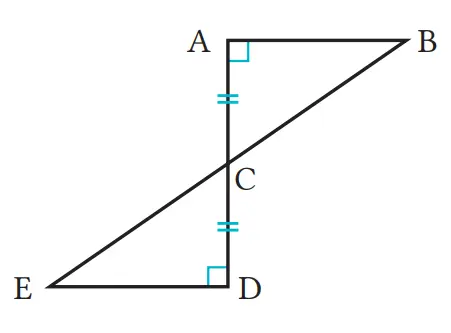
Jawaban:
Dari asumsi pada ΔACB dan ΔDCE, maka
AC = DC ①
∠A = ∠D = 90° ②
Karena sudut bertolak belakang sama, maka
∠ACB = ∠DCE ③
Dari (1), (2), dan (3), satu set sisi dan sudut di kedua ujungnya sama, maka
ΔACB ≅ ΔDCE
Karena sisi-sisi bersesuaian dari bangun yang kongruen adalah sama, maka
AB = DE
(2) Pada Metode Thales, ia memisalkan ∠BAC dan ∠EDC sebesar 90°. Bagian (a) , (b) , (c) , dan (d) berikut merupakan pernyataan-pernyataan terkait ∠BAC dan ∠EDC. Pilih pernyataanpernyataan yang benar.
(a) Hanya bila kedua sudut ∠BAC dan ∠EDC sebesar 90°, maka jarak ke kapal dapat kita tentukan dengan menggunakan ∆ABC ≅ ∆DEC.
(b) Jika ∠BAC = ∠CDE, maka jarak ke kapal dapat kita tentukan dengan ∆ABC ≅ ∆DEC meskipun besar sudutnya tidak 90°.
(c) Jika ∠BAC= 90°, maka jarak ke kapal dapat kita tentukan dengan menggunakan ∆ABC ≅ ∆DEC berapa pun besar ∠EDC.
(d) Meskipun ∠BAC dan ∠EDC tidak sama, jarak ke kapal dapat kita tentukan dengan menggunakan ∆ABC ≅ ∆DEC.
Jawaban:
(b) Jika ∠BAC = ∠CDE, maka jarak ke kapal dapat kita tentukan dengan ∆ABC ≅ ∆DEC meskipun besar sudutnya tidak 90°.
Penjelasan dan Hal yang Perlu Diperhatikan
1. Penggunaan 1
Thales dikatakan telah menggunakan kekongruenan segitiga untuk menemukan jarak dari darat ke kapal yang tidak dapat diukur secara langsung. Soal ini dapat melihat sifat-sifat bilangan yang digunakan di sana dengan membaca metode Thales ini.
(1) adalah soal yang membaca ide metode Thales, memahami bahwa jarak ke kapal dapat kita hitung dengan menggunakan kekongruenan segitiga, dan membuktikannya.
(2) adalah soal yang mempertimbangkan bagaimana mengatur kondisi sudut BAC dan sudut EDC untuk menemukan jarak ke kapal dengan memahami pengembangan metode Thales. Di sini, perlu untuk melihat kembali metode pemecahan masalah dan berpikir secara progresif. Pilih salah satu yang dinyatakan dengan benar berdasarkan kondisi kekongruenan segitiga.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
