ohgreat.id-Jawaban Soal Ringkasan dan Pendalaman Materi halaman 252 Menggunakan Data Matematika SMP Kelas 7 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 252. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 7 Menggunakan Data. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Soal Ringkasan
- 1.1 Gagasan Utama
- 1.1.1 (1) Berdasarkan data banyaknya penjualan baju setiap ukuran per tahun, sebuah perusahaan baju akan memutuskan ukuran baju yang mana yang perlu diproduksi lebih banyak pada tahun depan.
- 1.1.2 (2) Berdasarkan data sebelumnya mengenai hasil pertandingan lari 500 m beregu antara dua tim, buatlah perkiraan tim mana yang akan menang pada pertandingan mendatang.
- 1.1.3 (3) 15 siswa dalam suatu kelas bermain lempar bola tangan. Hasil lemparannya diukur dan dicatat. Berdasarkan catatan tersebut, selidiki apakah lemparanmu termasuk dalam 7 terbaik.
- 1.1.4 (1) 510.000.000 km² (luas permukaan Bumi)
- 1.1.5 (2) 0,0350 mm (ukuran serbuk sari cemara)
- 1.2 Penerapan
- 1.3 Penggunaan Praktis
- 1.3.1 (1) Berdasarkan dua histogram di atas, nampak bahwa banyaknya lompatan kedua pemain ini sama banyak. Hitunglah berapa kali mereka melompat.
- 1.3.2 (2) Berdasarkan dua histogram tersebut, hitunglah rata-rata jarak lompatan setiap pemain.
- 1.3.3 (3) Bandingkanlah dua histogram tersebut. Berdasarkan sifat-sifatnya, jika akan dipilih satu pemain untuk pertandingan berikutnya, siapa yang dipilih? Jelaskan alasanmu dengan membandingkan sifat-sifat dua histogram tersebut.
- 1.1 Gagasan Utama
- 2 Pendalaman Materi
Soal Ringkasan
Gagasan Utama
1. Nilai manakah yang sesuai digunakan sebagai nilai representatif pada (1) – (3) Jelaskan alasanmu.
(1) Berdasarkan data banyaknya penjualan baju setiap ukuran per tahun, sebuah perusahaan baju akan memutuskan ukuran baju yang mana yang perlu diproduksi lebih banyak pada tahun depan.
Jawaban:
Modus
(Contoh)
Ukuran yang paling laris tahun ini kita harapkan laris tahun depan, sehingga dapat kita gunakan modus.
(2) Berdasarkan data sebelumnya mengenai hasil pertandingan lari 500 m beregu antara dua tim, buatlah perkiraan tim mana yang akan menang pada pertandingan mendatang.
Jawaban:
Rata-rata
(Contoh)
Tim dengan catatan anggota rata-rata yang baik juga akan memiliki waktu estafet total yang lebih baik, jadi gunakan nilai rata-rata.
(3) 15 siswa dalam suatu kelas bermain lempar bola tangan. Hasil lemparannya diukur dan dicatat. Berdasarkan catatan tersebut, selidiki apakah lemparanmu termasuk dalam 7 terbaik.
Jawaban:
Median
(Contoh)
Dalam hal ini, median adalah rekor kedelapan dari yang terbaik. Jika rekor tersebut di atas median, dapat dinilai bahwa termasuk dalam 7 orang teratas, jadi di sini digunakan median.
2. Nyatakanlah bilangan-bilangan signifikan dari nilai pendekatan berikut ini. Berapakah nilai absolut (mutlak) galat terbesar?
(1) 510.000.000 km² (luas permukaan Bumi)
Jawaban:
5,10 × 10^8 km2
Nilai absolut galat adalah 500000 km2 atau kurang
(2) 0,0350 mm (ukuran serbuk sari cemara)
Jawaban:
3,50 × 1/10² mm
Nilai absolut dari galat adalah 0,00005 mm atau kurang
Penerapan
Tabel distribusi frekuensi di samping ini merangkum waktu tempuh dari rumah ke sekolah siswa-siswa kelas VII dari Sekolah A dan Sekolah B. Frekuensi relatif untuk setiap interval kelas dari Sekolah A disajikan dengan diagram garis pada gambar di bawah. Jawablah pertanyaan berikut ini.
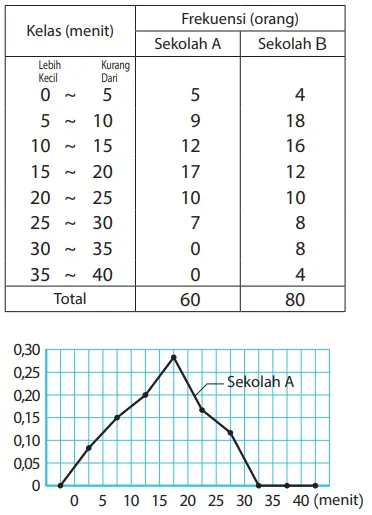
(1) Tentukan frekuensi relatif untuk setiap kelas di Sekolah B dan gambarlah grafik garis di samping kanan ini.
Jawaban:
Jika kita hitung frekuensi relatif tiap kelas B SMP,kita urutkan dari atas 0,050, 0,225, 0,200, 0,150, 0,125, 0,100, 0,100, 0,050
Oleh karena itu, garis poligonal frekuensinya adalah sebagai berikut.

(2) Apa perbedaan antara dua kumpulan data? Berikan paling sedikit dua perbedaan.
Jawaban:
a. Di sekolah menengah pertama A, puncak (modus) lebih dekat ke kanan.
b. Distribusi sekolah menengah pertama B tersebar di jangkauan yang lebih luas.
c. Ada lebih banyak siswa di SMP B yang menghabiskan lebih banyak waktu untuk pergi ke sekolah.
Penggunaan Praktis
1. Di antara dua pemain A dan B dipilih yang akan diajukan untuk pertandingan lompat ski berikutnya. Histogram berikut ini merangkum data lompatan pada kompetisi yang telah dilakukan selama ini. Jawablah (1) – (3).
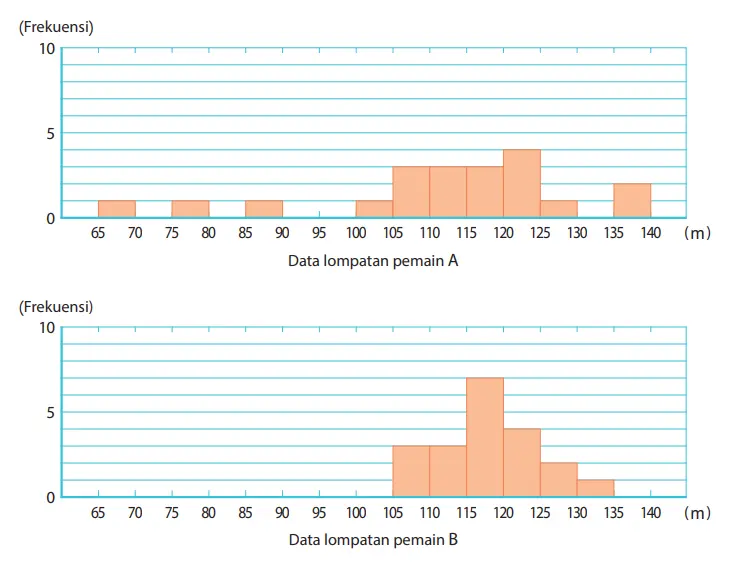
(1) Berdasarkan dua histogram di atas, nampak bahwa banyaknya lompatan kedua pemain ini sama banyak. Hitunglah berapa kali mereka melompat.
Jawaban:
20 kali
(2) Berdasarkan dua histogram tersebut, hitunglah rata-rata jarak lompatan setiap pemain.
Jawaban:
Tabel berikut menunjukkan catatan atlet A dan atlet B dalam tabel distribusi frekuensi.
Catatan Atlet A
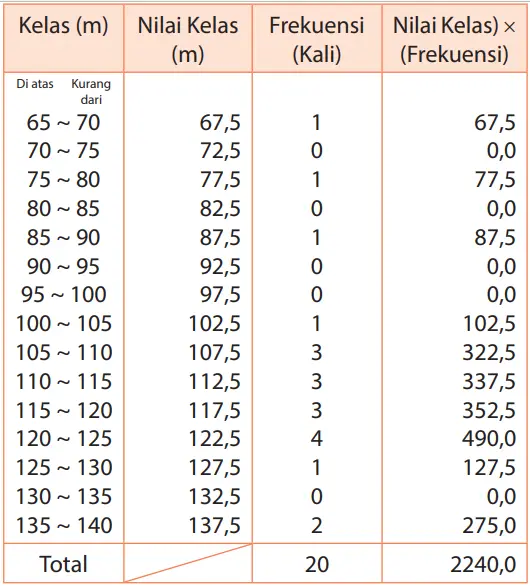
Dari 2240 : 20 = 112, maka 112 m
Catatan Atlet B
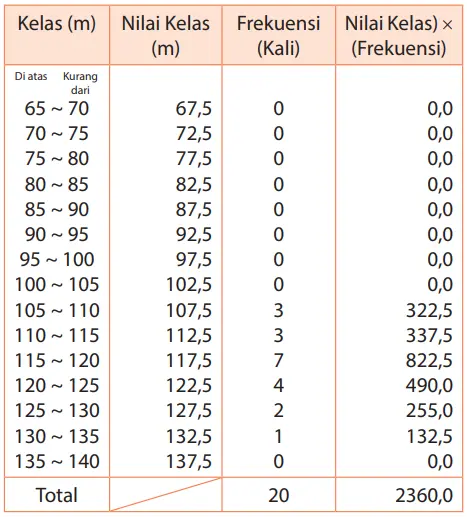
Dari 2360 : 20 = 118, maka 118 m
(3) Bandingkanlah dua histogram tersebut. Berdasarkan sifat-sifatnya, jika akan dipilih satu pemain untuk pertandingan berikutnya, siapa yang dipilih? Jelaskan alasanmu dengan membandingkan sifat-sifat dua histogram tersebut.
Jawaban:
Jika memilih atlet A
Meski terdapat sebaran pada catatan hasil atlet A, nilai kelas terbesar yang mana termasuk kelas di mana ada nilai terbesar adalah 137,5m. Nilai tersebut adalah lebih besar dari nilai kelas terbesar yang mana termasuk kelas di mana ada nilai terbesar pada kelas B yaitu 132,5 m, oleh karenanya dapat kita pikirkan bahwa pada pertandingan selanjutnya ada kemungkinan bisa lompat lebih jauh, menjadi alasannya.
Jika Anda memilih Atlet B.
a. Karena nilai rata-rata 118 m untuk pemain B lebih baik daripada nilai rata-rata 112 m untuk pemain A, hasil yang stabil dan baik dapat kita harapkan.
b. Nilai kelas yang temasuk di dalamnya nilai terkecil pada atlet B yaitu 107,5m adalah lebih besar dari nilai kelas yang termasuk di dalamnya nilai terkecil atlet A, yaitu 67,5 m, oleh karena itu dapat kita pikirkan bahwa pada pertandingan selanjutnya akan dapat melompat lebih jauh.
Pendalaman Materi
Piramida Populasi
Histogram di bawah ini menunjukkan populasi berdasarkan kelompok umur di Jepang tahun 1950 dan 2000. Dalam tabel dipisahkan juga berdasarkan jenis kelamin. Histogram di bawah ini disebut “piramida populasi.”
Data tahun 1950 menunjukkan ’piramida ekspansif’ (melebar ke bawah) disebabkan menurunnya laju kelahiran. Di sisi lain, piramida populasi tahun 2000 merupakan ‘piramida konstruktif ‘ (melebar di tengah).
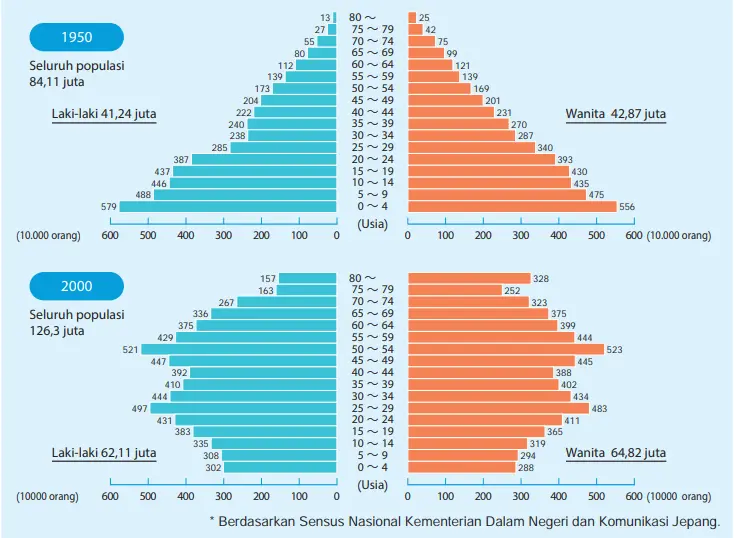
1. Pada distribusi populasi tahun 1950 dan tahun 2000, bandingkan kelompok usia yang mempunyai frekuensi terbesar.
Jawaban:
a. 1950 … 0-4 tahun baik untuk pria maupun wanita
b. 2000 … 50-54 tahun baik untuk pria maupun wanita
2 Bandingkanlah rasio populasi usia sampai 14 tahun dengan masing-masing kelompok usia lainnya. Bandingkanlah rasio populasi yang usianya paling sedikit 65 tahun.
Jawaban:
Persentase penduduk di bawah usia 14 tahun
<1950>
2979 ÷ 8411 = 0,3541 … (sekitar 35%)
<tahun 2000>
1846 ÷ 12693 = 0,1454 … (sekitar 15%)
Pada tahun 2000 proporsi penduduk di bawah usia 14 tahun mengalami penurunan yang cukup signifikan dibandingkan tahun 1950.
<1950>
416 ÷ 8411 = 0,0494 … (sekitar 5%)
<tahun 2000>
2201 ÷ 12693 = 0,1734 … (sekitar 17%)
Pada tahun 2000, proporsi penduduk usia 65 tahun ke atas meningkat secara signifikan dibandingkan tahun 1950.
3. Jika laju kelahiran terus menurun, dapatkah kamu perkirakan bagaimana bentuk histogram tahun 2050?
Jawaban:
Dapat Kita perkirakan menjadi segitiga terbalik.
Penjelasan:
Biasanya jumlah kelahiran besar, dan seiring bertambahnya usia, populasinya menurun karena kematian. Karena alasan ini, grafik tersebut menjadi piramida segitiga, yang disebut “piramida penduduk”. Namun, yang sering terlihat di negara maju seperti Jepang bukanlah jenis piramida melainkan jenis pot karena pengaruh angka kelahiran yang menurun.
Mereka yang berusia 0-4 tahun pada tahun 1950 berusia 50-54 tahun pada tahun 2000. Pada grafik tahun 2000, fenomena “menurunnya angka kelahiran” dapat kita lihat dari kenyataan bahwa jumlah penduduk di bawah kelompok umur ini semakin menurun. Selain itu, ada gunung yang memuncak pada kelompok umur 25-29 tahun yang kita anggap sebagai generasi anak-anak pada kelompok umur 50-54 tahun. Mereka juga disebut “generasi baby boomer” dan “baby boomer junior”.
Selanjutnya Kita perkirakan bahwa angka kelahiran akan terus menurun dalam 50 tahun, dan angka kelahiran akan mendekati bentuk segitiga terbalik.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
