ohgreat.id-Jawaban Soal Menerapkan Perbandingan Senilai dan Perbandingan Berbalik Nilai halaman 152 Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 152. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 4　Perbandingan Senilai dan Perbandingan Berbalik Nilai. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Menerapkan Perbandingan Senilai dan Perbandingan Berbalik Nilai

Siswa mampu mengidentifikasi hal-hal di sekilingnya yang mempunyai hubungan perbandingan senilai dan perbandingan berbalik nilai.

1. Sebuah perusahaan mampu memproduksi 5 gulung tisu kamar mandi dari 30 kotak susu bekas. Jika y gulung dihasilkan dari x kotak susu bekas, jawablah pertanyaan-pertanyaan berikut ini.

(1) Nyatakanlah hubungan antara x dan y dalam persamaan.

Jawaban:

Karena y sebanding dengan x,
Mensubstitusi x = 30, y = 5 pada y = ax,

5 = 30a
a = 1/6

Oleh karena itu rumus yang akan kita dapat adalah

y = 1/6x

(2) Berapa gulung tisu dapat dibuat oleh perusahaan tersebut dari 132 kotak susu bekas?

Jawaban:

y = 1/6x

y = 1/6 × 132 = 22

Contoh 2

Sebuah timbangan ditunjukkan pada gambar di sebelah kanan. Sebuah baterai digantung di salah satu sisi dan anak timbangan di sisi lainnya. Jarak baterai ke titik tumpu selalu tetap. Apabila baterai kita ganti dengan berat yang berbeda maka jarak anak timbangan ke titik tumpu menyesuaikan sedemikian hingga seimbang. Ketika anak timbangan kita teliti, hubungan antara berat x g dan jarak ke titik tumpu y cm, kita peroleh tabel di bawah ini.

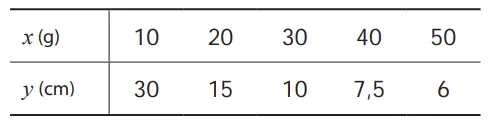
Dari tabel di atas, hasil kali x dengan y yang bersesuaian adalah tetap. Jadi, y berbanding terbalik dengan x.

2. Jawablah pertanyaan terkait Contoh 2 berikut ini.

(1) Nyatakanlah hubungan antara x dan y dalam persamaan.

Jawaban:

Karena hasil kali xy = 300 adalah konstan, maka dapat dipikirkan bahwa yberbanding terbalik terhadap x. Pada saat ini, persamaan perbandingan berbalik nilai adalah y = 300/x

(2) Ketika menggantung anak timbangan seberat 60 g pada sebelah kanan titik tumpu, berapa cm jarak anak timbangan tersebut dari titik tumpu agar seimbang?

Jawaban:

Jika pada persamaan (1), nilai x kita ganti menjadi x = 60, maka y = 300/60 = 5

Jawab: 5cm

(3) Jika menggantung anak timbangan sejauh 12 cm dari titik tumpu, berapa g beratnya?

Jawaban:

Persamaan perbandingan berbalik nilai y = 300/x dapat juga kita nyatakan dengan xy = 300. Jika pada persamaan ini, nilai y kita ganti dengan y = 12, maka

12x = 300
x = 25

Jawaban 25 g

3. Seperti ditunjukkan pada gambar di bawah ini, ada dua gerigi A dan B yang berputar saling berkait. A memiliki 30 gigi dan berputar 6 kali per detik. Untuk gerigi B, kita bisa memasang beberapa gerigi yang cocok.

(1) Jika gerigi B memiliki 60 gigi, berapa kali B berputar dalam satu detik?

Jawaban:

Karena gerigi A dan gerigi B hanya terkait pada jumlah gigi yang sama, maka dalam 1 detik, maju bersama sebanyak 30 × 6 = 180 saja. Oleh karena itu, jumlah putaran gerigi B dalam 1 detik adalah 180 : 60 = 3, maka berputar sebanyak 3 putaran.

Jawab: 3 putaran

(2) Jika banyaknya gigi B adalah x dan jumlah putaran dalam satu detik adalah y, nyatakanlah hubungan antara x dan y dalam persamaan.

Jawaban:

Dengan pola pikir yang sama seperti pada (1), dari xy = 180, kita dapat y = 180/x

Contoh 3

Diketahui sebuah persegi ABCD seperti ditunjukkan pada gambar di samping ini. Titik P bergerak dari titik A sepanjang sisi AB. Jika AP adalah x cm dan luas segitiga APD adalah y cm2, dapatkah disimpulkan bahwa y berbanding lurus dengan x? Atau dapatkah disimpulkan y berbanding terbalik dengan x?

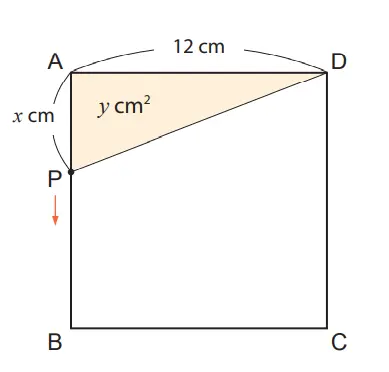
Penyelesaian:

Luas segitiga APD adalah

y = × x × 12

Jadi, y = 6x Karena persamaan merupakan perbandingan langsung, maka y berbanding lurus dengan x.

Jawab: y berbanding lurus dengan x

4. Jawablah pertanyaan-pertanyaan di bawah ini berdasarkan Contoh 3.

(1) Hitunglah luas segitiga APD jika P bergerak 5 cm dari A.

Jawaban:

Jika pada persamaan y = 6x, nilai x kita ganti dengan x = 5, maka

y = 6 x 5= 30

Jawab 30 cm2

(2) Tentukan domain dan jangkauan.

Jawaban:

<Domain x>

Karena titik P bergerak dari A ke B, dengan AB = 12cm, maka 0 ≤ x ≤ 12

<Jangkauan y>

Luas segitiga APD, pada saat titik P berada di A adalah terkecil, yaitu 0 cm2

Pada saat titik P berada di B adalah terbesar, yaitu y = 6 × 12 = 72, karenanya, 72 cm2

Oleh karena itu, 0 ≤ y ≤ 72

5. Diberikan sebuah persegi ABCD seperti ditunjukkan pada gambar di samping ini. Tititk P bergerak dari titik A sepanjang sisi AB. Tititk Q bergerak dari titik A sepanjang sisi AD sedemikian hingga luas APQ sama dengan 6 cm2. Jika AP adalah x cm dan AQ adalah y cm, jawablah pertanyaan berikut ini.

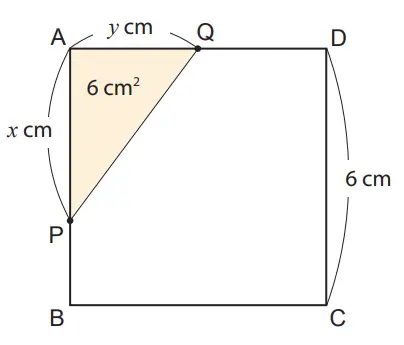
(1) Nyatakanlah hubungan antara x dan y dalam persamaan.

Jawaban:

Karena luas segitiga APQ adalah selalu 6 cm2, maka 1/2 xy = 6 sehingga y = 12/4

(2) Dapatkah disimpulkan y berbanding lurus dengan x? Atau dapatkah disimpulkan y berbanding terbalik dengan x?

Jawaban:

Karena dapat kita nyatakan dengan y = 12/x , maka y berbanding terbalik terhadap x

(3) Tentukan domain dan jangkauan.

Jawaban:

2 ≤ x ≤ 6, 2 ≤ y ≤ 6

Penerapan Grafik

Contoh 4

Dua bersaudara berangkat dari rumah bersama-sama menuju stasiun kereta yang jaraknya 1.200 m. Untuk setiap anak, y adalah jarak yang telah ditempuh x menit setelah berangkat. Grafik di bawah ini menunjukkan hubungan antara x dan y untuk anak yang lebih tua (kakak). Hitunglah kecepatan berjalan kakak.

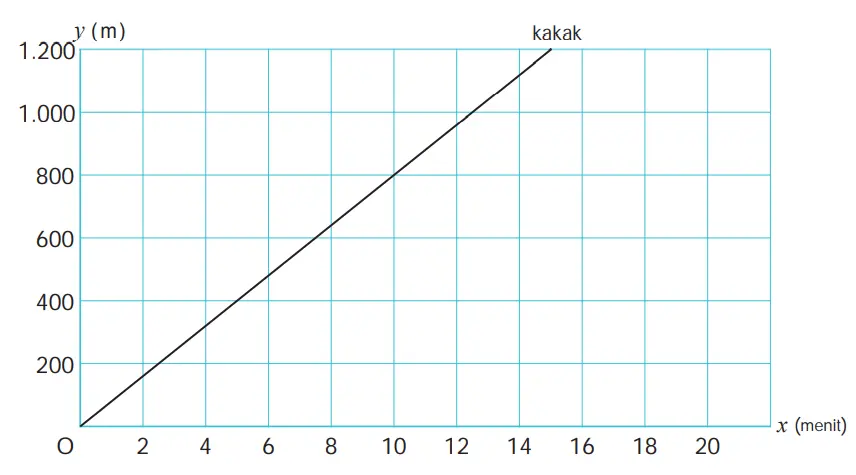
penyelesaian

Berdasarkan gambar di atas, kakak berjalan 800 m dalam waktu 10 menit

karena (Jarak) : (Waktu) = (Kecepatan).

800 : 10 = 80

Jadi, kecepatan kakak adalah 80 m per menit.

Jawab: 80 m per menit

6. Jawablah pertanyaan berikut ini berdasarkan Contoh 4.

(1) Untuk kakak, nyatakanlah hubungan antara x dan y dalam persamaan.

Jawaban:

Karena kecepatan berjalan kakak adalah 80m per menit, maka y = 80x

(2) Gambarlah grafik yang menyatakan hubungan antara x dan y untuk adik yang berjalan dengan kecepatan 60 m per menit. Kemudian, nyatakanlah hubungan antara x dan y dalam persamaan.

Jawaban:

y = 60x

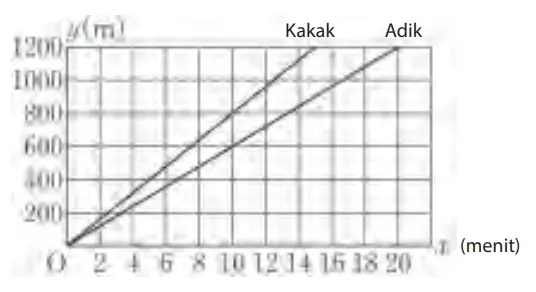
(3) Berapa menit waktu yang adik perlukan untuk sampai di stasiun?

Jawaban:

20 menit setelahnya

(4) Ketika kakak sampai stasiun, berapa jarak kakak dari adiknya?

Jawaban:

Karena kakak sampai di stasiun 15 menit setelah meninggalkan rumah, maka jika nilai x pada y = 60x di persamaan adik kita isikan dengan x = 15, sehingga

y = 60 × 15 = 900
1.200 – 900 = 300

Jawaban: Pada titik 300 meter di depan stasiun

Mari Mencoba

Pada Contoh 4, gambarlah grafik yang menunjukkan hubungan x dan y untuk adik jika dia berjalan dengan kecepatan 100 m per menit. Kemudian, buatlah soal berdasarkan grafik tersebut dan juga grafik untuk kakak.

Jawaban:

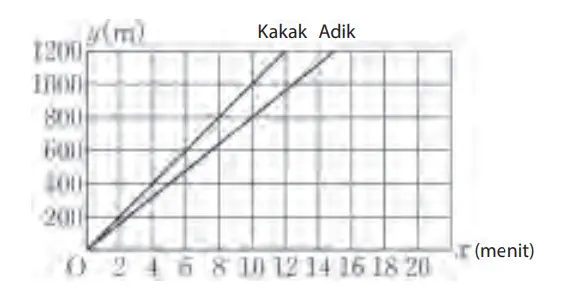
(Contoh soal)

Pada saat adik tiba di stasiun, berada pada titik berapa meter sebelum stasiun keretakah kakak?

(Jawab: titik 240 meter sebelum stasiun)

Pada menit ke berapa setelah berangkatkah perbedaan jarak tempuh antara kakak dan adik menjadi 200 meter?

(Jawab: 10 menit setelahnya)

 

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***