ohgreat.id-Jawaban Soal Kedudukan Garis dan Bidang pada Ruanghalaman 199 Sifat-Sifat Bangun Ruang Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 199. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 6 Bangun Ruang. Selanjutnya pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Sifat-Sifat Bangun Ruang

Kedudukan Garis dan Bidang pada Ruang

Siswa memahami letak kedudukan garis dan bidang pada ruang

Menentukan Bidang

Q. Terdapat dua titik A dan B pada bidang P. Ada berapa banyak garis yang dapat dilukis melalui A dan B?

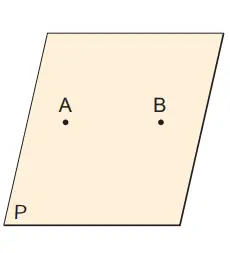
Jawaban:

Garis yang melewati titik A jumlahnya bisa mencapai tidak terhingga.

Garis yang melewati dua titik A dan B hanya ada satu

catatan: Ketika kita mengatakan bidang, pada umumnya yang dimaksud adalah bidang yang diperluas ke segala arah. Selanjutnya Kita menggunakan simbol P dan disebut bidang P.

1. Terdapat tripod yang digunakan untuk menyangga kamera. Selanjutnya Jelaskan mengapa tripod memiliki tiga kaki.

Jawaban:

Karena tiga titik yang tidak berada di satu garis lurus adalah sebuah bidang, maka tempat mendaratnya ketiga kakinya sudah pasti merupakan sebuah bidang, sehingga stabil karena selalu berada di posisi yang pas dengan lantai atau permukaan tanah.

Dua Garis

Q. Diketahui prisma segi empat pada gambar berikut ini.

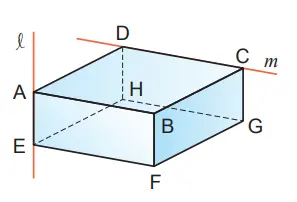
(1) Rusuk manakah yang sejajar dengan rusuk AE?
Rusuk manakah yang tegak lurus dengan rusuk AE?

Jawaban:

a. Rusuk yang sejajar dengan rusuk AE
…rusuk BF, CG, DH

b. Rusuk yang berpotongan dengan rusuk AE
…rusuk AB, AD, EF, EH

(2) Adakah rusuk yang tidak sejajar dan juga tidak berpotongan dengan rusuk AE?

Jawaban:

Ada (Rusuk BC,FG,DC,HG)

2. Rusuk manakah dari prisma segiempat pada yang merupakan garis-garis yang bersilangan dengan rusuk EF?

Jawaban:

Rusuk AD, BC, DH, CG

Garis dan Bidang

Q. Selidikilah hubungan letak kedudukan antara permukaan EFGH dan setiap rusuk prisma segiempat di samping ini. Kelompokkan rusuk-rusuk berdasarkan hubungan letak kedudukannya.

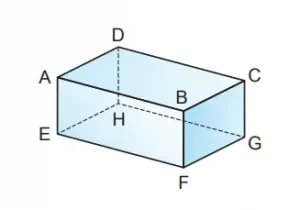
Jawaban:

Dapat dibagi ke tiga kelompok di bawah ini

a. Rusuk yang ada di bidang EFGH
… rusuk EF, FG, HG, EH

b. Rusuk yang berpotongan tegak lurus
terhadap bidang EFGH
…rusuk AE, BF, CG, DH

c. Rusuk yang sejajar dengan bidang EFGH
…rusuk AB, BC, DC, AD

Jika garis l dan bidang P tidak berpotongan, maka mereka katakan sejajar dan ditulis l//P.

Ada tiga macam kedudukan antara sebuah garis dan sebuah bidang sebagai berikut

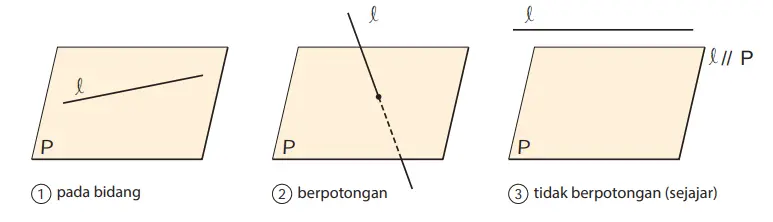
Q. Sebuah buku kita letakkan di atas meja pada posisi berdiri dan kita buka sampulnya (lihat gambar di samping kanan). Selanjutnya bagaimana hubungan tempat kedudukan AB dan BC?

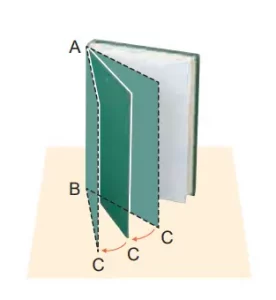
Jawaban:

Berada di posisi manapun rusuk BC, rusuk AB dan BC adalah tegak lurus.

3. Sebuah tongkat tipis berdiri tegak lurus di atas meja dibantu sekumpulan penggaris siku-siku, seperti pada gambar di samping. Diskusikan berapa banyak penggaris siku-siku yang kita butuhkan?

Jawaban:

Jika dua penggaris segitiga kita lletakkan dengan posisi seperti di bawah ini, maka tongkat akan dapat berdiri tegak lurus.

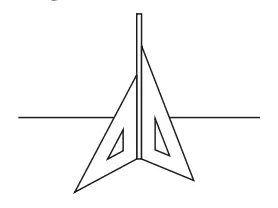
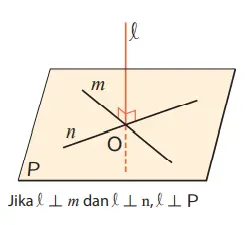
Jika garis l memotong bidang P di titik Q dan tegak lurus pada dua garis pada bidang P, maka garis l dan bidang P saling tegak lurus.

4. Rusuk manakah dari prisma segitiga ini yang sejajar dengan permukaan ADEB?Permukaan manakah yang tegak lurus pada BE?

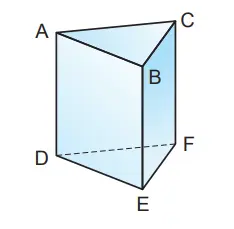
Jawaban:

a. Rusuk yang sejajar dengan bidang ADEB…
Rusuk CF

b. Bidang yang tegak lurus dengan rusuk BE
…Bidang ABC, DEF

Dua Bidang

Q. Perhatikan prisma segi empat pada Q di halaman sebelumnya. Permukaan manakah yang sejajar dengan permukaan ABCD? Permukaan manakah yang tegak lurus?

Jawaban:

a. Bidang yang sejajar dengan bidan ABCD
…bidang EFGH

b. Bidang yang tegak lurus dengan bidang ABCD
…bidang AEFB, BFGC, DHGC, AEHD

Ketika dua bidang P dan Q tidak berpotongan, kita katakan bahwa bidang P dan Q sejajar , dan ditulis P//Q.  Selanjutnya ada dua macam kedudukan dua bidang pada ruang, seperti pada gambar berikut ini.

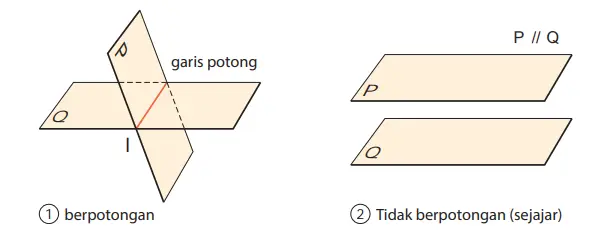
Jika dua bidang P dan Q berpotongan, garis yang terbentuk disebut garis potong.

5. Bagaimana hubungan letak kedudukan garis n dan m, yang merupakan garis potong bidang R pada dua bidang yang sejajar, yaitu P dan Q?

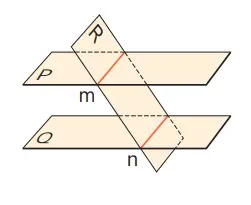
Jawaban:

m//n sejajar

Alasan

m dan n masing-masingnya adalah garis pada bidang P dan Q yang saling sejajar, oleh karenanya tidak berpotongan. Di sisi lain, m dan n adalah garis pada bidang R yang sama, oleh karenanya, m//n.

Q. Ketika kita membuka laptop, seperti pada gambar di samping, bagaimanakah mengukur besarnya sudut yang terbuka?

Jawaban:

Tarik 2 garis yang tegak lurus pada garis potong seperti pada gambar. Selanjutnya, ukurlah sudut yang terbentuk.

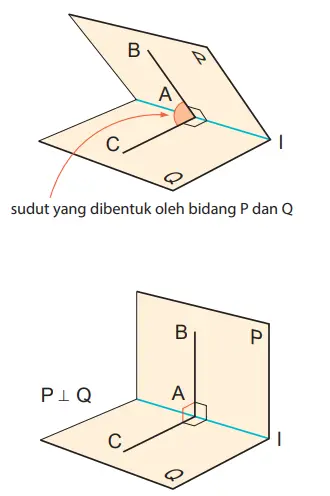
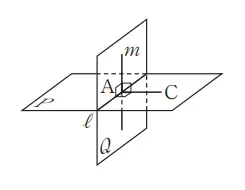
Ketika dua bidang P dan Q berpotongan, kita ambil A salah satu titik pada garis potong l dan tarik garis sinar AB pada Q dan garis sinar AC pada Q yang memenuhi AB ⊥ l dan AC ⊥ l. Akhirnya ∠ BAC adalah sudut yang terbentuk oleh bidang P dan Q.

Ketika BAC = 90º, maka kita katakan bahwa bidang P dan Q saling tegak lurus dan kita tulis P ⊥ Q.

6. Pada gambar di samping ini, garis m tegak lurus pada bidang P. Jika Q adalah bidang yang memuat garis m, maka bagaimanakah kedudukan bidang P dan Q?

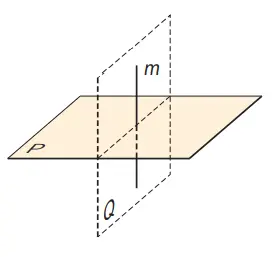
Jawaban:

Tegak lurus (P ⊥ Q)

Alasan

Seperti pada gambar di bawah ini, misalkan titik potong garis m dan bidang P adalah A, dan garis potong bidang P dan Q adalah l. Karena l adalah garis pada P yang melewati A, maka
m ⊥ l ①

Selanjutnya, pada P tariklah garis AC membentuk AC ⊥l . Dari sini,
AC ⊥ l ②

Selain itu, karena AC adalah garis yang melalui A pada P, maka
m ⊥ AC ③

Akhirnya Dari ①, ②, ③ kita dapatkan bahwa P ⊥ Q

Jarak pada Ruang

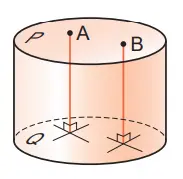
7. Titik A dan B berada pada alas tabung, seperti kita perlihatkan pada gambar di samping kanan. Selanjutnya bandingkanlah jarak A ke alas Q dan titik B ke alas Q.

Jawaban:

Kedua jaraknya sama.

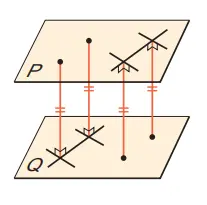
Ketika dua bidang P dan Q sejajar, jarak setiap titik pada salah satu bidang ke bidang yang lain adalah sama. Jarak ini kita sebut sebagai jarak antara dua bidang P dan Q yang saling sejajar. Sama halnya dengan prisma dan tabung, jarak antara dua alasnya disebut tinggi. Begitu juga dengan kerucut dan limas, jarak antara titik puncak ke alas disebut tinggi.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***