ohgreat.id-Jawaban Soal Bagaimana Menyelesaikan Persamaan halaman 101 Persamaan dan Pertidaksamaan Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 101. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 3 Persamaan Linear. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Persamaan dan Pertidaksamaan

Bagaimana Menyelesaikan Persamaan

Mampu menyelesaikan persamaan dengan cara yang lebih mudah.

Q. Sifat-sifat persamaan yang mana yang digunakan pada kedua persamaan berikut ini?

a. x – 9 = 3 ; x – 9 + 9 = 3 + 9
x = 3 + 9 = 12

b. 2x = 6 + x
2x –x = 6 + x – x ; 2x – x = 6
x = 6

Jawaban:

A. Menggunakan sifat persamaan 1 (tambahkan 9 di kedua sisi).

I. Menggunakan sifat persamaan 2 (kurangkan x di kedua sisi)

1. Ketika membandingkan (1) dan (2) di Q a , Wida mengamati berikut ini.

Pada 1 , sisi kiri memiliki suku -9. Ketika ditambahkan 9 ke kedua sisi, maka -9 pada sisi kiri akan hilang. Sedangkan di 2 , 9 muncul di sisi kanan.

Untuk b , apa yang kamu amati ketika membandingkan 1 dan 2 ?

Jawaban:

Sebaiknya sembunyikan dulu rumus pada baris kedua a dan b. Pertama, bacalah dulu penjelasan Wilda tentang a, kemudian simak perubahannya pada bagian berikut ini. Dengan mengacu pada penjelasan Wilda, alangkah baiknya jika kita dapat menjelaskan bahwa di 2 , alih-alih menjelaskan suku x di sisi kanan menghilang, lebih baik menjelaskan istilah -x muncul di sisi kiri.

2. Pada a dan b , bagaimana kita mendapatkan 2 langsung dari 1 ? Jelaskan menggunakan pemahamanmu di 1

a. x – 9 = 3
x = 3 + 9

b. 2x = 6 + x
2x – x = 6

Jawaban:

Menjelaskan dua poin dengan kalimat sendiri:

1) Pindahkan suku dari sisi kiri (sisi kanan) ke sisi kanan (sisi kiri).

2) Ubah tanda saat memindahkan suku.

3. Selesaikan setiap persamaan menggunakan cara yang kamu pelajari di 1 dan 2 .

(1) x + 7 = -3

(2) -2x = 8 – 3x

Kita belajar dari halaman sebelumnya, bahwa dalam persamaan kita dapat memindahkan suku-suku dari satu sisi ke sisi yang lain. Hal ini disebut mentranspos atau memindahkan suku-suku.

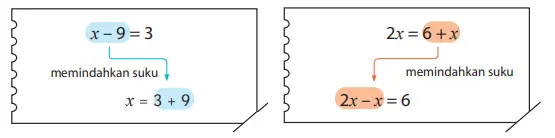
Ingat, ketika sebuah suku berpindah sisi, tanda yang ada di depannya berubah menjadi kebalikannya.

 

Menyelesaikan Persamaan Menggunakan Ide Memindahkan Suku-Suku

Contoh 1

3x + 5 = -4

Pindahkan 5 dari sisi kiri ke sisi kanan,

3x = -4 – 5
3x = -9
x = -3

1. Pada Contoh 1, periksa apakah -3 merupakan penyelesaian dengan substitusi x = -3.

Jawaban:

Sisi kiri = 3 × (-3) + 5 = -4

Sisi kanan = -4

Oleh karena itu, karena (sisi kiri) = (sisi kanan), maka -3 adalah penyelesaian dari persamaan 3x + 5 = -4

Dalam memindahkan suku-suku untuk menyelesaikan persamaan, letakkan semua suku-suku huruf ke sisi kiri dan semua suku-suku bilangan ke sisi kanan.

2. Selesaikan

(1) 2x + 1 = 9

(2) 4x – 5 = -13

(3) 3x = -2x – 15

(4) 2x = 3x – 8

Jawaban:

(1) 2x + 1 = 9
2x = 9 -1
x = 8 : 2
x = 4

(2) 4x – 5 = -13
4x = -13 + 5
x = -8 : 4
x = -2

(3) 3x = -2x – 15
3x + 2x = -15
5 x = -15
x = -15 : 5
x = -3

(4) 2x = 3x = – 8
2x -3x = -8
-x = -8
x = 8

Pertanyaan Serupa

Selesaikan persamaan berikut

(1) 3x + 4 = -5

(3) 5x = 7x- 8

(2) -2x – 7 = 11

(4) x = -4x + 10

Jawaban:

(1) x = -3

(2) x = -9

(3) x = 4

(4) x = 2

3. Selesaikanlah.

(1) 6x – 12 = 3x

(2) 7x – 3 = 5x + 7

(3) 5x + 15 = -2x + 1

(4) 3 + 7x = 4x – 6

(5) 8 + 2x = 3x – 1

(6) 3x + 2 = x + 4

Jawaban:

(1) x = 4 (4) x = -3

(2) x = 5 (5) x = 9

(3) x = -2 (6) x = – 1/2

Persamaan dengan Tanda Kurung

Contoh 4 Selesaikanlah 5x – 2(x – 3) = 3.

Hapus tanda kurung dengan menerapkan sifat distributif.

5x – 2(x – 3) = 3
5x – 2x + 6 = 3
Pindahkan 6 ke sisi kanan.
5x – 2x = 3 – 6
3x = –3
x = –1
Jawab : x = -1

4. Selesaikanlah.

(1) 2(x – 5) + 1 = 7

(2) 4x – 7(x + 2) = -5

(3) -2(x + 3) = 5x + 8

(4) 3(x – 8) = -6(x + 4)

Jawaban:

(1) 2(x – 5) + 1 = 7
2x – 10 + 1 = 7
2x = 7 + 9
x = 8

(2) 4x – 7(x + 2) = -5
4x – 7x – 14 = -5
-3 x = -5 + 14
x = 9 : 3
x = -3
Selesaikan no 3 dan 4 seperti diatas

(3) x = -2

(4) x = 0

Persamaan dengan Desimal dan Pecahan

Contoh 5 Selesaikanlah 2,3x = 0,5x + 9.

Ubahlah koefisien persamaan di atas menjadi bilangan bulat dengan mengalikan kedua sisi dengan 10.

2,3x = 0,5x + 9

Kalikan kedua sisi dengan 10, diperoleh 2,3x × 10 = (0,5x + 9) × 10
23x = 5x + 90
23x – 5x = 90
18x = 90
x = 5

Ketika persamaan memuat pecahan, maka dapat juga diselesaikan dengan mengalikan kedua sisi dengan faktor pengali bersama dari penyebut-penyebutnya. Tujuannya adalah mengubahnya menjadi kalimat matematika tanpa pecahan.

5. Selesaikanlah.

(1) 0,4x + 2 = 0,3x

(2) 0,25x = 0,2x – 0,1

Jawaban:

(1) Kalikan dengan 10 pada kedua sisi 4x+ 20 = 3x
Ketika ini terpecahkan hasilnya, x = -20

(2) Kalikan dengan 100 pada kedua sisi25x = 20x – 10
Ketika ini terpecahkan hasilnya, x = -2

Contoh 6 Selesaikanlah 5/6x = 2 = 1/3x

Ubahlah koefisiennya menjadi bilangan bulat dengan mengalikan kedua sisi dengan 6.

Mengalikan kedua sisi persamaan dengan faktor pengali bersama dari penyebut-penyebutnya yang bertujuan mengubah menjadi persamaan tanpa pecahan disebut pembatalan penyebut pecahan.

6. Selesaikanlah.

(1) 1/2x = 2/5x – 1

(2) 2/3x – 1/2 = 5/6x + 2

(3) (x – 3)/2 = -4

(4) (x + 2)/6 = (x – 3)/4

Jawaban:

(1) Kalikan dengan 10 pada kedua sisi
5x = 4x – 10
Ketika ini terpecahkan hasilnya, x = -10

(2) Kalikan dengan 6 pada kedua sisi
4x – 3 = x + 12
Ketika ini terpecahkan hasilnya, x = 5

(3) Kalikan dengan 2 pada kedua sisi
x – 3 = -8
Ketika ini terpecahkan hasilnya, x = -5

(4) Kalikan dengan 12 pada kedua sisi
2x + 4 = 3x – 9
Ketika ini terpecahkan hasilnya, x = 13

7. Mia menyelesaikan persamaan 2/3x = 1/2x – 7 dengan cara yang ditunjukkan di samping ini. Apakah benar? Koreksilah kesalahan yang kamu temukan.

Jawaban:

Salah

2/3x = 1/2x – 7

Kalikan dengan 6 pada kedua sisi

2/3x x 6 = (1/2x – 7) x 6
4x = 3x – 42
x = -42

Langkah-Langkah Penyelesaian Persamaan

1. Hapus tanda kurung dan hilangkan penyebut jika diperlukan.

2. Pindahkan suku-suku huruf ke sisi kiri dan suku-suku bilangan ke sisi kanan.

3. Ubahlah persamaan ke dalam bentuk ax = b, (a 0)

4. Bagi kedua sisi persamaan dengan a (koefisien x).

Untuk semua persamaan dalam x yang telah kita selesaikan dengan cara mengubah semua suku-suku sisi kiri, maka diperoleh ax + b = 0, (a ≠ 0) dimana sisi kiri adalah bentuk aljabar linear dalam x.

Persamaan tersebut dinamakan persamaan linear.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***