ohgreat.id-Jawaban Sifat-Sifat Segitiga Sama Kaki halaman 138 Segitiga Sama Kaki Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 138. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Segitiga Sama Kaki

Sifat-Sifat Segitiga Sama Kaki

Q. Jenis segitiga apakah segitiga sama kaki itu?

Jawaban:

Segitiga yang kedua sisinya adalah sama panjang

Segitiga yang kedua sudutnya adalah sama besar

Kita telah mempelajari hal-hal berikut di Sekolah Dasar.

(1) Segitiga yang memiliki dua sisi yang sama panjang disebut segitiga sama kaki.

(2) Segitiga sama kaki memiliki dua sudut yang sama besar.

Suatu pernyataan yang menjelaskan makna dari suatu kata disebut definisi. Kita dapat menggunakan definisi sebagai landasan bernalar dalam proses pembuktian.

Mendefinisikan Segitiga sama kaki sebagai berikut.

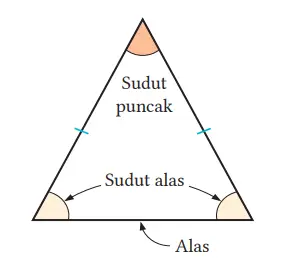
Segitiga yang memiliki dua sisi yang sama panjang disebut segitiga sama kaki.

Pada segitiga sama kaki, sudut yang terbentuk oleh dua sisi yang sama panjang disebut sudut puncak. Sisi di hadapan sudut puncak yaitu alas, dan sudut-sudut pada ujung-ujung alas yaitu sudut alas.

Soal 1

Carilah ∠x dan ∠y pada gambar-gambar berikut.

(1) BA = BC

(2) CB = CA, BA = BD

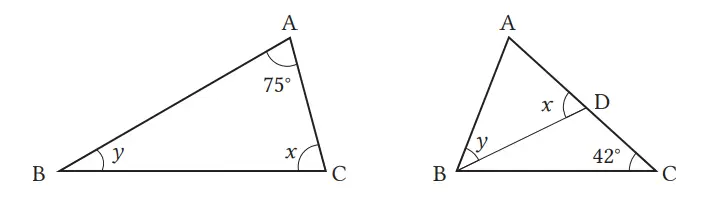
Jawaban:

(1) ∠x = 75°, ∠y = 30°

(2) ∠x = 69°, ∠y = 42°

Soal 2.

Jika kita gunakan ∆ABD ≅ ∆ACD seperti ditunjukkan pada pembuktian Contoh 1 di halaman sebelumnya, kita dapat pula membuktikan BD = CD dan AD ⊥ BC. Isilah [] dan lengkapi pembuktian berikut.

Jawaban:

∠ADC, 90°

Pernyataan yang terbukti di Soal 2 dapat merangkumnya sebagai sebuah teorema berikut.

Teorema: Garis Bagi
Sudut Puncak Segitiga Sama Kaki

Garis bagi sudut puncak segitiga sama kaki adalah garis bagi tegak lurus alasnya.

Soal 3

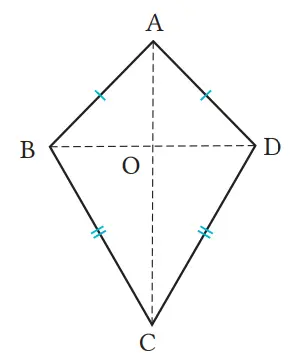
Pada segi empat ABCD diketahui AB = AD dan BC = DC. Misalkan O titik potong diagonal AC dan BD. Buktikan (1) , kemudian (2) berikut.

(1) ∠BAC = ∠DAC

(2) AC garis bagi tegak lurus dengan ruas garis BD

Jawaban:

(1) Dari asumsi di ΔABC dan ΔADC

AB = AD ①

BC = DC ②

Juga, AC sisi persekutuan ③

Dari (1), (2), dan (3), dan aturan kekongruenan sisi-sisi-sisi, maka

ΔABC ≅ ΔADC

Oleh karena itu, ∠BAC = ∠DAC

(2) Dari AB = AD, maka ΔABD adalah segitiga sama kaki.

Dari ∠BAC = ∠DAC, maka AC adalah garis bagi dari sudut puncak ΔABD. Akibatnya, alas BD terbagi secara tegak lurus menjadi dua segmen yang sama. Jadi, AC adalah garis bagi tegak lurus dengan ruas garis BD.

Soal 4

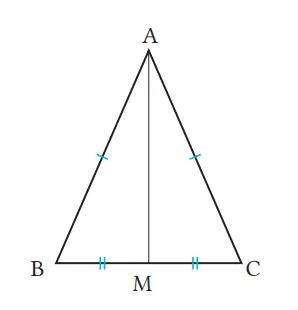
Buktikan bahwa dua sudut alas dari segitiga sama kaki adalah sama besar. Gunakan cara dengan membuat ruas garis AM yang dibentuk dengan menghubungkan titik puncak A dan titik M yang merupakan titik tengah sisi alas BC, seperti pada segitiga sama kaki ABC di gambar sebelah kanan.

Jawaban:

⟨Asumsi⟩ AB = AC, BM = CM

⟨Kesimpulan⟩ ∠B = ∠C

⟨Pembuktian⟩

Dari asumsi ΔABM dan ΔACM, AB = AC ①

BM = CM ②

Juga, AM adalah sisi persekutuan ③

Dari (1), (2), dan (3), dan aturan kekongruenan sisi-sisi-sisi, maka

ΔABM ≅ ΔACM.

Oleh karena itu, ∠B = ∠C.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***