ohgreat.id-Jawaban Penjelasan Menggunakan Bentuk Aljabar halaman 16 Menggunakan Bentuk Aljabar Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 16. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 1 Menyederhanakan Bentuk Aljabar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Menggunakan Bentuk Aljabar

1. Penjelasan Menggunakan Bentuk Aljabar

Peserta didik dapat menjelaskan sifat-sifat bilangan dan gambar geometri menggunakan bentuk aljabar.

Q. Tentukan jumlah dari tiga bilangan bulat berurutan, seperti 6, 7, dan 8. Diskusikan sifat-sifat apakah yang dimiliki oleh penjumlahan tiga bilangan tersebut.

6 + 7 + 8 = []

10 + 11 + 12 = []

23 + 24 + 25 = []

Jawaban:

6 + 7 + 8 = 21

10 + 11 + 12 = 33

23 + 24 + 25 = 72

Sifat yang dimiliki oleh penjumlahan tiga bilangan

a. Kelipatan 3

b. Kelipatan 3 dari bilangan tengah

Menjelaskan secara deduktif bahwa jumlah 3 bilangan bulat berurutan adalah kelipatan 3. Pada prosesnya termasuk kegiatan sebagai berikut.

(1) Memilih 3 bilangan bulat berurutan dengan menggunakan variabel n. Ketiga bilangan bulat yang dipilih adalah n, n + 1, n + 2.

(2) Menghitung jumlahnya, dan hasilnya dinyatakan dalam bentuk 3(n + 1).

(3) Membaca bahwa 3 (n + 1) dianggap sebagai 3 × (bilangan bulat), dan hasilnya adalah kelipatan 3.

(4) Memahami bahwa jumlah 3 bilangan bulat berurutan adalah kelipatan 3.

Dengan demikian, pada saat menjelaskan dengan menggunakan variabel, digunakan bentuk aljabar, perhitungan dan pembacaan secara komprehensif.

Terkait sifat yang ditemukan dalam Q, kita tidak dapat memeriksa apakah sifat tersebut berlaku untuk semua bilangan dengan hanya melakukan perhitungan terhadap bilangan-bilangan tertentu. Dalam hal ini, dengan menggunakan bentuk aljabar, kita dapat membuktikan bahwa sifat tersebut berlaku untuk semua bilangan.

Contoh 1

Jelaskan dengan menggunakan bentuk aljabar, mengapa jumlah dari tiga bilangan bulat berurutan adalah kelipatan 3.

Cara

Nyatakan 3 bilangan bulat berurutan dengan menggunakan sebuah variabel dan tunjukkan bahwa jumlahnya berupa 3 × (bilangan bulat).

Penyelesaian

Jika kita misalkan bilangan terkecil adalah n, maka 3 bilangan bulat berurutan dapat kita nyatakan dengan n, n + 1, n + 2. Jumlah ketiganya adalah

n + (n + 1) + (n + 2)

= 3n + 3

= 3(n + 1)

n + 1 adalah bilangan bulat, sehingga 3(n + 1) merupakan kelipatan 3. Dengan demikian, jumlah dari 3 bilangan bulat berurutan adalah kelipatan 3.

Catatan: Ketika kita berbicara tentang kelipatan sebuah bilangan, kelipatan dengan 0 atau bilangan negatif juga diperhitungkan sebagai kelipatan bilangan tersebut.

Soal 1

Dari penyelesaian Contoh 1 pada halaman sebelumnya, apa lagi yang dapat kita ketahui tentang jumlah dari 3 bilangan bulat berurutan selain kelipatan 3?

Jawaban:

3 kali lipat bilangan tengah.

S0al 2

Jelaskan Contoh 1 pada halaman sebelumnya dengan memisalkan n sebagai bilangan yang di tengah.

Jawaban:

3 bilangan bulat yang berurutan, jika digit tengah dianggap n, maka ditulis, n – 1, n, n + 1. Jumlah semuanya adalah

(n – 1) + n + (n + 1) = 3n

Perhatikan bahwa 3n adalah kelipatan 3 karena n adalah bilangan bulat. Jadi, jumlah 3 bilangan bulat berurutan adalah kelipatan 3. Pastikan urutan perhitungan diawali dengan menghilangkan tanda kurung, lalu mengoperasikan suku sejenis dengan sifat distributif.

Q. Pertama diberikan suatu bilangan asli dua digit. Bilangan kedua diperoleh dari bilangan pertama, tetapi dengan menukar letak digit satuan dengan digit puluhannya. Jumlah kedua bilangan tersebut merupakan kelipatan bilangan tertentu. Periksa kelipatan berapakah hasil penjumlahannya.

21 + 12 = [] 35 + 53 = [] 47 + 74 = []

Jawaban:

33, 88, 121

(Contoh) 60 + 6 = 66

98 + 89 = 187

Keduanya kelipatan 11

Untuk suatu bilangan asli dua digit, dengan memisalkan a sebagai digit puluhan dan b sebagai digit satuan maka bilangan tersebut dapat dinyatakan sebagai 10a + b.

Soal 3

Apa yang dapat kita katakan tentang selisih antara suatu bilangan asli dua digit dengan bilangan yang diperoleh dari menukar digit puluhan dengan satuan pada bilangan pertama? Jelaskan menggunakan bentuk aljabar.

Jawaban:

Menjadi kelipatan 9

(Penjelasan)

Misalkan a adalah angka puluhan dari bilangan asli dua digit dan b adalah digit satuan, maka bilangan asli tersebut adalah 10a + b. Bilangan asli yang digitnya bertukar tempat adalah 10b + a. Selisih 2 bilangan ini adalah

(10a + b) – (10b + a) = 9a – 9b
= 9 (a – b)

(a − b) adalah bilangan bulat, maka 9(a − b) adalah kelipatan 9. Oleh karena itu, bilangan asli dua digit dan bilangan asli yang diperoleh dari menukar tempat digit satuan dengan digit puluhan, selisihnya merupakan kelipatan 9.

Komunikasi

Q. Dari jumlah pasangan bilangan berikut, mana yang menghasilkan bilangan ganjil dan mana yang menghasilkan bilangan genap?

(1) (Ganjil) + (Genap)

(2) (Genap) + (Genap)

(3) (Ganjil) + (Ganjil)

Jawaban:

(1) Bilangan ganjil

(2) Bilangan genap

(3) Bilangan genap

Bilangan genap adalah bilangan yang habis dibagi 2. Dengan kata lain, bilangan genap merupakan kelipatan 2. Oleh karena itu, jika kita misalkan m adalah bilangan bulat, maka bilangan genap dapat dinyatakan dengan 2m. Bilangan ganjil tidak habis dibagi 2. Dengan kata lain, bilangan ganjil selalu lebih besar satu dari suatu bilangan genap. Oleh karena itu, jika kita misalkan n adalah bilangan bulat, maka bilangan ganjil dapat dinyatakan dengan 2n + 1.

1. Dewi menjelaskan mengapa jumlah bilangan genap dan bilangan ganjil hasilnya adalah bilangan ganjil seperti berikut ini.

Cara Dewi

Jika kita menjumlahkan bilangan ganjil 2n + 1 ke bilangan genap 2m, maka kita memperoleh dua pasangan sebanyak (m + n) dan tersisa 1 lingkaran yang tidak berpasangan, seperti terlihat pada gambar di kanan. Oleh karena itu, jumlah bilangan genap dan bilangan ganjil adalah bilangan ganjil.

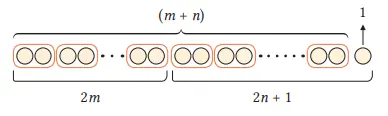
Dengan menggunakan Cara Dewi, jelaskan hasil 2 dan 3 pada Q.

Jawaban:

(2) Dengan menambahkan bilangan genap 2n kepada 2m, maka terdapat (m + n) pasangan, seperti yang ditunjukkan pada gambar berikut. Oleh karena itu, jumlah bilangan genap dan bilangan genap adalah bilangan genap.

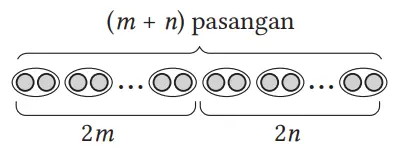
(3) Dengan menambahkan bilangan ganjil 2n + 1 kepada 2m + 1, maka terdapat (m + n) pasangan dan sisa 2 lingkaran tidak berpasangan, seperti yang ditunjukkan pada Gambar 1. Jika disusun ulang, maka dapat dibuat sebanyak (m + n + 1) pasangan, seperti yang ditunjukkan pada Gambar 2. Oleh karena itu, jumlah bilangan ganjil dengan bilangan ganjil adalah bilangan genap.

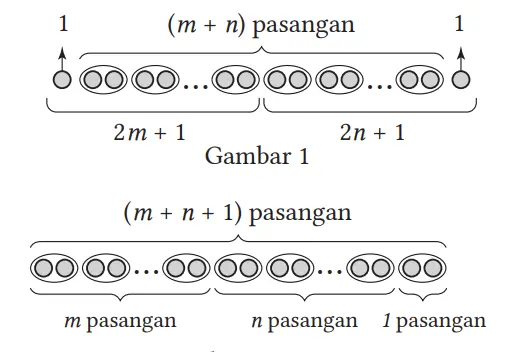
Jumlah bilangan ganjil dengan bilangan ganjil adalah bilangan genap.

2. Heru menjelaskan mengapa jumlah dari bilangan genap dan bilangan ganjil adalah bilangan ganjil dengan menggunakan bentuk aljabar seperti berikut. Lengkapi penjelasan Heru dengan mengisi dengan bentuk aljabar atau kata-kata yang tepat.

Cara Heru

Jika kita misalkan m dan n adalah bilangan-bilangan bulat, maka bilangan genap dapat dinyatakan dengan 2m, dan bilangan ganjil dapat dinyatakan dengan 2n + 1. Jumlah bilangan genap dan bilangan ganjil adalah

2m + (2n + 1)
= 2m + 2n + 1
= 2 ( ) + 1

Karena [ ] bilangan bulat, maka [ ] adalah bilangan ganjil. Oleh karena itu,[ ].

Jawaban:

Karena [m + n] bilangan bulat, maka [m + n] adalah bilangan ganjil. Oleh karena itu,[ 2(m + n) + 1]. Jumlah bilangan genap dan bilangan ganjil adalah bilangan ganjil.

3. Asep menjelaskan 1 dan 2 di atas, dengan memisalkan bilangan genap sebagai 2m dan bilangan ganjil dengan 2m + 1. Jelaskan apakah cara Asep itu benar atau tidak.

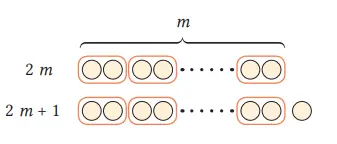
Jawaban:

2m, 2m + 1 akan menjadi bilangan genap dan bilangan ganjil berurutan, seperti 4 dan 5(m = 2), 10 dan 11(m = 5). Tidak mungkin menjelaskan jumlah dari semua bilangan genap dan bilangan ganjil.

4. Dengan menggunakan bentuk aljabar, tuliskan penjelasan (2) dan (3) pada Q di halaman sebelumnya. Coba jelaskan kepada temanmu dengan cara tersebut.

Jawaban:

(2) Jika m, n adalah bilangan bulat, maka dua bilangan genapnya adalah 2m, 2n.

Jumlah dua bilangan genapnya adalah 2m + 2n = 2(m + n)

(m + n) adalah bilangan bulat, maka 2(m + n) adalah bilangan genap. Oleh karena itu, jumlah bilangan genap dengan bilangan genap adalah bilangan genap.

(3) Jika m, n adalah bilangan bulat, maka dua bilangan ganjilnya adalah 2m + 1, 2n + 1.

Jumlah dua bilangan ganjilnya adalah

(2m + 1) + (2n + 1)
= 2m + 2n + 2
= 2(m + n + 1)

m + n + 1 adalah bilangan bulat, maka 2(m + n + 1) adalah bilangan genap. Oleh karena itu, jumlah bilangan ganjil dengan bilangan ganjil adalah bilangan genap.

5. Dengan meninjau kembali apa yang telah kamu pelajari hingga saat ini, buatlah kesimpulan terhadap tiap pertanyaan berikut.

(1) Bagaimana cara menyatakan pernyataan berikut menggunakan variabel: “3 bilangan bulat berurutan”, “Bilangan asli dua digit”, “Bilangan genap dan bilangan ganjil”, “Kelipatan 3”, dan lain-lain?

Jawaban:

“Tiga bilangan bulat yang berurutan” misalnya disimbolkan oleh variabel n, n + 1, n + 2 dengan n adalah bilangan bulat. Boleh juga disimbolkan oleh n −1, n, n + 1.

“Bilangan asli dua digit” misalnya disimbolkan oleh 10a + b jika digit puluhannya adalah a dan digit satuannya adalah b.

“Bilangan genap, bilangan ganjil” misalnya secara berturut-turut disimbolkan oleh variabel 2m, 2n + 1 dengan m dan n adalah bilangan bulat.

“Kelipatan 3” misalnya disimbolkan oleh variabel 3n dengan n adalah bilangan bulat.

(2) Mengapa penjelasannya jauh lebih baik jika menggunakan bentuk aljabar?

Jawaban:

Tidak semua bilangan riil dapat dihitung dalam segala kasus mengenai apakah bilangan tersebut membentuk sifat tertentu atau tidak.Namun apabila menggunakan bentuk aljabar, hal tersebut dapat dijelaskan secara umum.

Soal 4

Pada 2 di halaman 3, jelaskan bagaimana kita menebak hari ulang tahun.

Jawaban:

Tanggal lahir dianggap bulan x tanggal y.

10(7x + y) + 3(10x – 3y) = 100x + y

Jika terbentuk bilangan 3 digit, maka bulan ulang tahun adalah digit ratusan dan tanggal ulang tahun adalah digit pada puluhan dan satuan.

Jika terbentuk bilangan 4 digit, maka bulan ulang tahun adalah 2 digit pertama dan tanggal ulang tahun adalah 2 digit pada terakhir.

Soal 5

Jika diketahui AP = PQ = QR = RB seperti pada gambar di sebelah kanan, mengapa jumlah panjang 4 busur setengah lingkaran dengan diameter AP, PQ, QR, dan RB adalah sama dengan panjang busur setengah lingkaran dengan diameter AB? Jelaskan menggunakan bentuk aljabar.

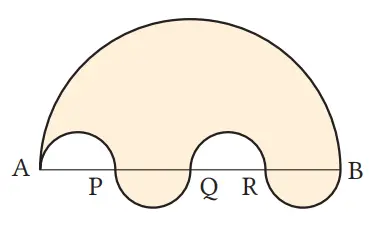
Jawaban:

Jika AP = a, maka panjangnya busur setengah lingkaran dengan diameter AP.

(π × a) × 1/2 = 1/2πa

AP = PQ = QR = RB, maka panjang dari 4 busur setengah lingkaran yang masing-masing diameternya AP, PQ, QR, RB, adalah sama, dan jumlah keseluruhannya adalah

1/2πa × 4 = 2πa ①

Selain itu, AB = 4a, maka panjang busur setengah lingkaran yang berdiameter AB adalah

(π × 4a) × 1/2 = 2πa ②

Dari ① dan ②

AP + PQ + QR + RB = AB

Oleh karena itu, panjang dari 4 busur setengah lingkaran yang masing-masing diameternya AP, PQ, QR, RB, adalah sama dengan panjangnya busur setengah lingkaran dengan diameter AB.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***