ohgreat.id-Jawaban Pendalaman Materi halaman 167 Bab 5 Segitiga dan Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 167. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Pendalaman Materi

Mari Pikirkan dengan
Mengubah Syaratnya

Pada Soal 4 halaman 165, hal berikut ini telah dibuktikan.

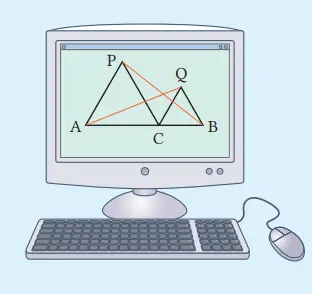
Jika kita ambil titik C pada ruas garis AB dan membuat segitiga sama sisi ACP dan CBQ secara berturut-turut dengan menggunakan sisi AC dan BC sebagai sisi, maka AQ = PB.

1. Bila kita rotasi ∆CBQ dengan titik C sebagai pusat rotasinya, mari kita selidiki apakah AQ = PB.

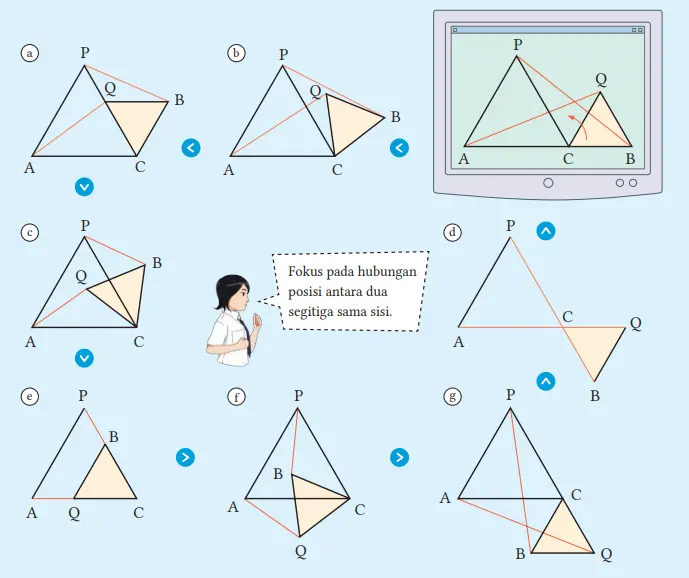
Jawaban:

Bahkan jika ΔCBQ diputar di sekitar titik C sebagai pusat rotasi, AQ = PB berlaku.

2. Mari buktikan apa yang telah kita selidiki di bagian 1 di halaman sebelumnya. Sebagai contoh, pada kasus (c) , kita dapat membuktikan bahwa AQ = PB seperti berikut.

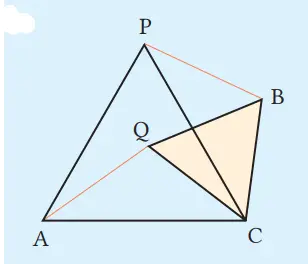
Bukti

Pada ∆QAC dan ∆BPC, berdasarkan yang diketahui, maka AC = PC 1, QC = BC 2

Selain itu, ∠ACQ = ∠ACP – ∠QCP = 60° – ∠QCP

Dan, ∠PCB = ∠QCB – ∠QCP = 60° – ∠QCP

Jadi, ∠ACQ = ∠PCB 3

Dari 1 , 2 , dan 3 , dan berdasarkan aturan kekongruenan Sisi-Sudut-Sisi,maka ∆QAC ≅ ∆BPC

Jadi, AQ = PB.

Mari kita buktikan bahwa AQ = PB pada kasus lain.

Jawaban:

⟨Pembuktian (a) ⟩

Pada ΔQAC dan ΔBPC, AC = PC, QC = BC

∠ACQ = 60° + ∠QCP = ∠PCB

Menurut aturan kekongruenan sisi-sudut-sisi, maka ΔQAC ≅ ΔBPC

Oleh karena itu, AQ = PB.

Pembuktian (b)

Seperti bukti (a) , kondisi sudut adalah ∠ACQ = 60° + ∠QCP = ∠PCB

Pembuktian (d)

AQ = AC + QC, PB = PC + BC
AC = PC, QC = BC

Oleh karena itu, AQ = PB.

Pembuktian (e)

Seperti bukti (a), kondisi sudutnya adalah ∠ACQ = 60° – ∠ACB = ∠PCB

Pembuktian (f)

Seperti bukti (a) , kondisi sudut adalah ∠ACQ = 60° – ∠ACB = ∠PCB

Pembuktian (g)

AQ = AC + QC, PB = PC + BC
AC = PC, QC = BC

Oleh karena itu, AQ = PB.

3. Seperti ditunjukkan pada gambar berikut, mari kita selidiki apa yang berlaku benar bila kita mengubah bagian kondisi pada nomor 4 di halaman 165. Buktikan!

(1) Ubah segitiga sama sisi menjadi persegi.

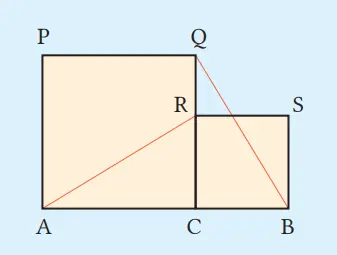
Jawaban:

AR = QB, berlaku

⟨Bukti⟩

Dari asumsi pada ΔACR dan ΔQCB,

AC = QC ①
CR = CB ②
∠ACR = ∠QCB ③

Dari (1), (2), dan (3), serta menurut aturan kekongruenan sisi-sudut-sisi, maka ΔACR ≅ ΔQCB

Oleh karena itu, AR = QB.

(2) Ambil titik C yang bukan pada ruas garis AB.

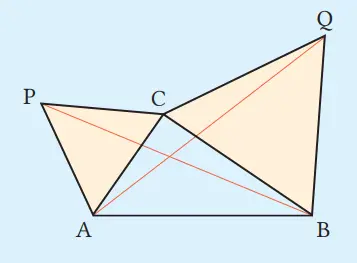
Jawaban:

PB = AQ, berlaku

⟨Bukti⟩

Dari asumsi pada ΔCPB dan ΔCAQ,

CP = CA ①
CB = CQ ②

Juga, ∠PCB = ∠PCA + ∠ACB = 60° + ∠ACB

∠ACQ = ∠BCQ + ∠ACB = 60° + ∠ACB

Oleh karena itu, ∠PCB = ∠ACQ ③

Dari (1), (2), dan (3), serta menurut aturan kekongruenan sisi-sudut-sisi, maka ΔCPB ≅ ΔCAQ

Oleh karena itu, PB = AQ.

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***