ohgreat.id-Jawaban Monom dan Polinom Serta Derajat dari Bentuk Aljabar halaman 4 Struktur dari Bentuk Aljabar Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 4. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 1 Menyederhanakan Bentuk Aljabar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Struktur dari Bentuk Aljabar
Bentuk Suku Tunggal (Monom) dan Suku Banyak (Polinom)
Q. Bentuk-bentuk aljabar (a) sampai (f) berikut menyatakan berbagai ukuran dari prisma tegak di samping
(a) 4x
(b) x²
(c) 2x + 2y
(d) xy
(e) 2x² + 4xy
(f) x²y
(1) Pikirkan jumlah suku yang dituliskan pada bentuk aljabar (perhatikan satuannya).
Jawaban:
a. Keliling (cm) satu persegi pada sisi kotak bagian bawah atau atas
b. Luas bagian bawah atau atas (cm²)
c. Keliling (cm) satu persegi panjang di bagian sisi tegak
d. Luas persegi panjang di bagian sisi tegak (cm²)
e. Luas permukaan (cm²)
f. Volume (cm³)
(2) Diskusikan bagaimana kita mengelompokkan bentuk aljabar tersebut berdasarkan ciri-cirinya.
Jawaban:
Dapat kita klasifikasikan berdasarkan bilangan atau variabel.
Bentuk aljabar dalam bentuk hasil kali antarbilangan atau antarvariabel, seperti 4x dan xy pada Q disebut suku tunggal (monom). Variabel atau bilangan suku satu, seperti y dan –6 disebut juga suku tunggal.
Bentuk-bentuk aljabar yang diperoleh dari hasil penjumlahan suku tunggal seperti 10x + 20 dan 2x + 2y disebut suku banyak (polinom). Setiap suku tunggal pada bentuk suku banyak disebut suku dari suku banyak.
Soal 1
Kelompokkan bentuk aljabar di (b) , (e) , dan (f) dari Q ke dalam bentuk suku tunggal dan bentuk suku banyak.
Jawaban:
Bentuk suku tunggal adalah (b) dan (f).
Bentuk suku banyak adalah (e).
Soal 2
Tentukan suku-suku dari suku banyak berikut ini.
(1) 5a + 1
(2) 7x – 8y
(3) 4x² + 7x – 9
Jawaban:
(1) 5a, 1
(2) 7x, (–8y)
(3) 4x², 7x, 9
Derajat dari Bentuk Aljabar
Q. Nyatakan tiap bentuk suku tunggal berikut dengan menggunakan tanda perkalian (×).
(1) 2x
(2) -3×2
(3) 5x2y
Jawaban:
(1) 2 x X
(2) -3 x X x X
(3) 5 x X x X x y
Banyaknya variabel yang dikalikan dalam suatu bentuk suku tunggal disebut derajat dari suku tunggal tersebut. Jika suku tunggal hanya memiliki satu variabel, maka konsep derajat sama dengan pangkat. Hati-hati jika variabelnya lebih dari satu.
Soal 3
Tentukan derajat dari bentuk suku tunggal berikut.
(1) -6a
(2) x²
(3) ½ ab
(4) -xy²
Jawaban:
(1) -6a ……… berderajat 1
(2) x² ……… berderajat 2
(3) ½ ab ……… berderajat 2
(4) -xy² ……… berderajat 3
Derajat dari bentuk suku banyak adalah derajat paling tinggi dari suku-suku bentuk suku banyak.
Catatan:
Kita dapat membandingkan derajat dari bentuk suku tunggal pada soal 3 (1), (2), (3), dan (4) menggunakan istilah “lebih dari” atau “kurang dari”, contohnya apakah derajatnya bentuk suku tunggal (1) lebih dari atau kurang dari derajatnya bentuk suku tunggal (2)?
contoh:
Pada bentuk suku banyak x² – 4x + 3, suku dengan derajat tertinggi adalah x2.
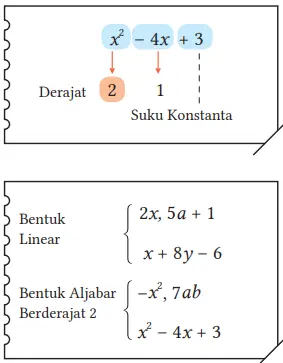
Suatu bentuk aljabar berderajat 1 disebut bentuk linear, bentuk aljabar berderajat 2 yang hanya memiliki satu variabel disebut bentuk kuadrat, dan seterusnya.
Soal 4
Berapakah derajat dari setiap bentuk aljabar (a) sampai (f) dari Q pada halaman sebelumnya?
Jawaban:
(a) 4x …………. Derajat 1
(b) x² …………. Derajat 2
(c) 2x + 2y …………. Derajat 1
(d) xy …………. Derajat 2
(e) 2x² + 4xy …………. Derajat 2
(f) x²y …………. Derajat 3
Pada bentuk suku tunggal, memahami tentang derajat dengan mengonfirmasi hal-hal berikut.
a. Bentuk suku tunggal adalah bentuk (bilangan) × (variabel).
b. Bagian bilangan disebut koefisien.
c. Derajat ditentukan oleh bagian variabel.
Saat mencari derajat dari suku banyak, dapat terjadi kesalahan, yaitu menjumlahkan derajat dari setiap suku. Ajarkan dengan cermat agar dapat dipahami dengan benar bahwa, “di antara derajat tiap suku pada polinom, derajat yang paling maksimum adalah derajat polinom”.
Seperti pada “Catatan”, derajat dari suku-sukunya dapat dibandingkan dengan “lebih dari” atau “kurang dari”.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
