ohgreat.id-Jawaban Mari Kita Periksa halaman 162 Garis Sejajar dan Luas Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 162. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Garis Sejajar dan Luas

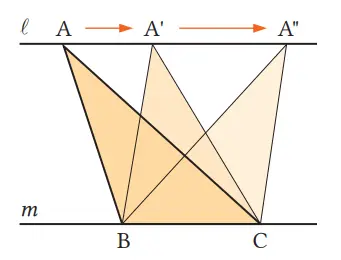
Q. Jika ℓ // m pada gambar di kanan, dan dengan memindahkan titik A dari ∆ABC searah tanda panah pada garis ℓ, maka apa yang tidak berubah meskipun bentuk segitiganya berubah?

Jawaban:

Tinggi dan luas dengan ruas garis BC sebagai alasnya.

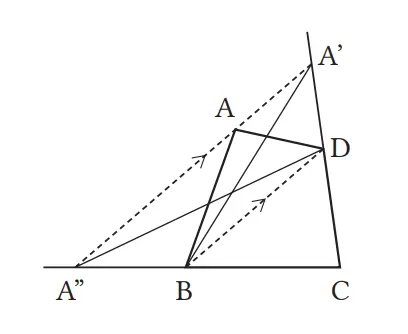
Untuk ∆ABC, ∆A’BC, dan ∆A”BC pada gambar di atas, alas BC merupakan alas persekutuan dan tingginya sama dengan jarak antara garis sejajar ℓ dan m. Dengan demikian, luas dari ketiga segitiga ini sama besar.

Soal 1

Jika kita misalkan O adalah titik potong antara kedua diagonal dari trapesium ABCD, dengan AD//BC, maka jawablah pertanyaan berikut.

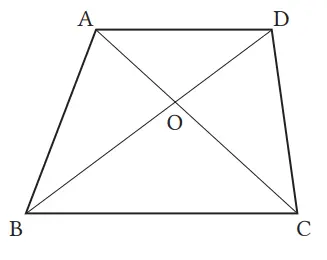
(1) Tentukan segitiga-segitiga mana saja yang berturut-turut memiliki luas yang sama dengan ∆ABC dan ∆ABD.

Jawaban:

Untuk BC dan AD // BC, maka luas ΔABC = luas ΔDBC

Untuk AD dan AD // BC, maka luas ΔABD = luas ΔACD

(2) Buktikan bahwa luas ∆ABO = luas ∆DCO.

Jawaban:

Luas ΔABO = luas ΔABC – luas ΔOBC ①

Luas ΔDCO = luas ΔDBC – luas ΔOBC ②

Dari ⑴, luas ΔABC = luas ΔDBC ③

Dari ①, ②, ③, maka luas ΔABO = luas ΔDCO

Contoh 1

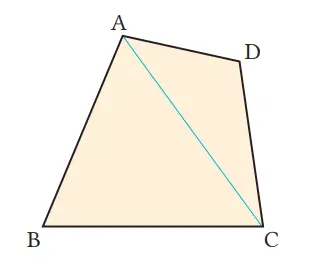
Buatlah sebuah segitiga yang memiliki luas yang sama dengan segi empat ABCD pada gambar di sebelah kanan.

Cara

Pandang AC sebagai alas ∆DAC, dan pindahkan titik D tanpa mengubah luas. Bila tiga titik B, C, dan D terletak pada satu garis, maka segi empat ABCD menjadi sebuah segitiga.

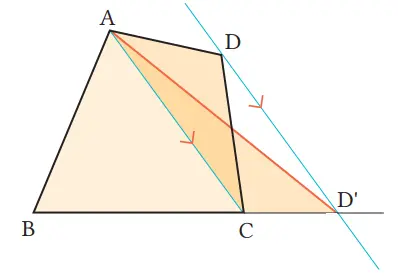
Proses

(1) Buat diagonal AC.

(2) Buat garis yang melalui D dan sejajar AC. Misalkan D’ titik potong dengan perpanjangan BC.

(3) Hubungkan titik A dan D’.

Soal 2

Pada Contoh 1 , buktikan bahwa luas segi empat ABCD = luas segi empat ∆ABD’.

Jawaban:

Luas persegi panjang ABCD = luas ΔABC + luas ΔDAC

Luas ΔABD’ = luas ΔABC + luas ΔD’ AC

Karena ΔDAC dan ΔD’AC memiliki sisi AC yang sama dan merupakan AC // DD’, maka luas ΔDAC = luas ΔD’AC

Oleh karena itu, luas segi empat ABCD = luas segi empat ABCD’.

Soal 3

Pada Contoh 1 , buat diagonal BD, dan buat suatu segitiga yang memiliki luas yang sama dengan segi empat ABCD.

Jawaban:

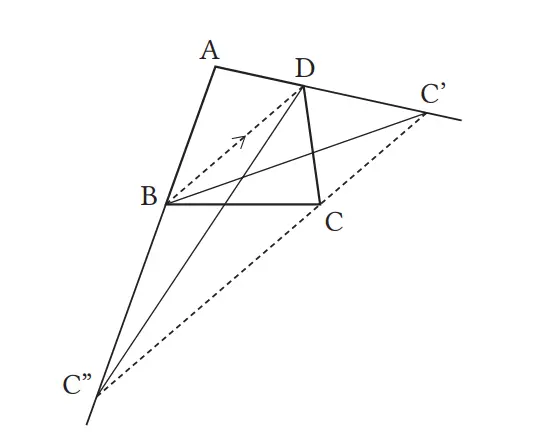
Soal  4

Seperti ditunjukkan pada gambar di sebelah kanan, suatu tanah dibagi ke dalam dua bagian a dan b dengan garis PQR sebagai batasnya. Tanpa mengubah luas tanah, buat garis yang melalui P untuk membuat batas lainnya.

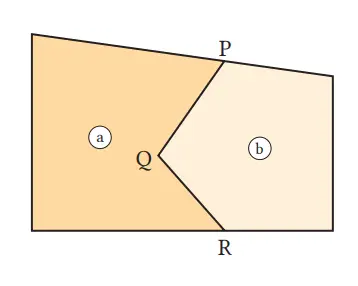
Jawaban

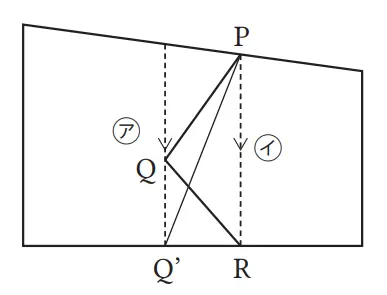
(1) Hubungkan titik P dan titik R.

(2) Gambarkan garis yang melewati titik Q dan sejajar dengan PR, dan anggap Q’ adalah perpotongan dengan sisi bawah.

(3) Batas lainnya adalah garis yang diperoleh dengan ‘menghubungkan P dan Q’.

Mari Kita Periksa

1. Garis Sejajar dan Luas

Pada gambar di kanan, jika AD//BC dan BM = CM, tentukan segitiga-segitiga yang memiliki luas yang sama dengan ∆ABM.

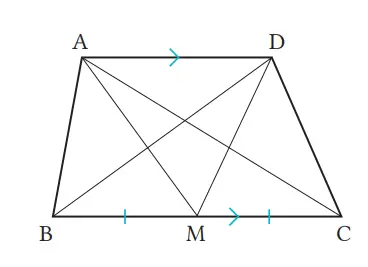
Jawaban:

Luas ΔABM = luas ΔDBM

(BM-nya sama, maka AD // BM)

Luas ΔABM = luas ΔDMC = luas ΔAMC

(Alasnya sama, yaitu BM = CM, tingginya sama, dan AD // BC) maka jawabannya adalah luas ΔDBM, luas ΔDMC, luas ΔAMC

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***