ohgreat.id-Jawaban Mari Kita Periksa halaman 160 Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 160. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Segi Empat
Mari Kita Periksa
1. SifatJajargenjang
Tuliskan definisi dari jajargenjang.
Jawaban:
Segi empat dengan 2 pasangan sisi yang sejajar
2. Sifat Jajargenjang
Jika E dan F masing-masing terletak pada sisi AD dan BC dari jajargenjang ABCD, sehingga AE = CF, maka buktikan bahwa BE = DF.
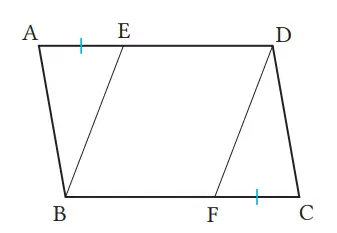
Jawaban:
Dari asumsi ΔABE dan ΔCDF, AE = CF ①
Karena sisi berlawanan dan sudut berhadapan pada jajargenjang masing-masing panjangnya sama, maka AB = CD dan ②
∠A = ∠C ③
Dari (1), (2), dan (3), serta menurut aturan kekongruenan sisi-sudut-sisi, maka ΔABE ≅ ΔCDF
Oleh karena itu, BE = DF.
3. Syarat untuk Jajargenjang
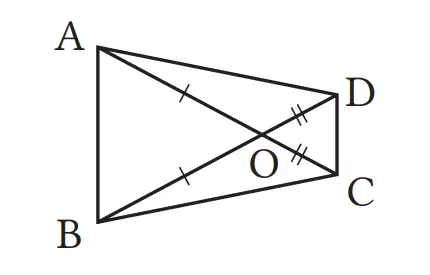
Dari kasus-kasus a , b , c , dan d berikut, kasus manakah yang mengakibatkan segi empat ABCD menjadi jajargenjang?
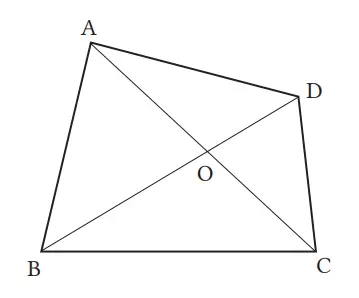
(a) AD // BC, AB = DC
(b) AB // DC, AB = DC
(c) AO = CO, BO = DO
(d) AO = BO, CO = DO
Jawaban:
((b) AB // DC, AB = DC , (c) AO = CO, BO = DO
(Contoh h penyangkal (a))
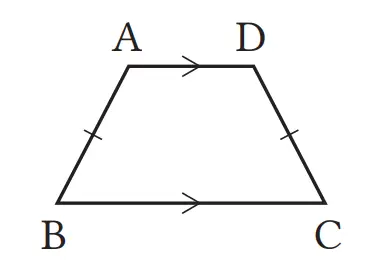
(Contoh penyangkal (d))
4. Syarat untuk Jajargenjang
Misalkan D dan E berturut-turut merupakan titik tengah dari sisi AB dan AC pada ∆ABC. Ambil titik F pada perpanjangan DE sehingga DE = EF. Jawablah pertanyaan berikut.
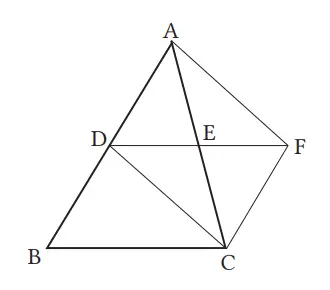
(1) Buktikan bahwa segi empat ADCF jajargenjang.
Jawaban:
Dari asumsi,
AE = CE (1)
DE = FE (2)
Dari (1) dan (2), segi empat ADCF adalah jajargenjang karena kedua diagonal berpotongan di titik tengahnya.
(2) Buktikan bahwa DF = BC.
Jawaban:
Dari (1), segi empat ADCF adalah jajargenjang,
jadi
AD // FC (1)
AD = FC (2)
Dari asumsi, AD = DB (3)
Dari (1), (2), dan (3), segi empat DBCF adalah jajargenjang karena DB // FC dan DB = FC. Sehingga, DF = BC.
5. Jajargenjang Khusus
Sifat-sifat apa yang dimiliki oleh diagonal-diagonal persegi? Tunjukkan jawabanmu dengan menggunakan gambar di kanan.
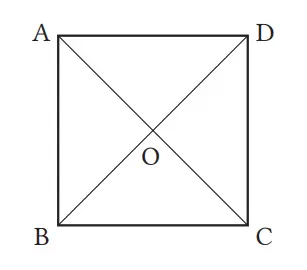
Jawaban:
AO = CO, BO = DO, AC = BD, AC⊥BD
(AO = CO = BO = DO, AC⊥BD
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
