ohgreat.id-Jawaban Latihan 8.3 halaman 228 Dua Kejadian A dan B Saling Lepas dan Tidak Saling Lepas Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMA/SMK Kelas 10 halaman 228. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMA/SMK Kelas 10 Kurikulum Merdeka Bab 8 Peluang. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Latihan 8.3

Gunakan aturan penjumlahan untuk soal-soal berikut mengenai sepasang dadu yang dilempar.

1. Tentukan peluang mendapatkan dua angka sama atau berjumlah 5.

a. Apakah kedua kejadian ini saling lepas atau tidak saling lepas?

b. Peluang mendapatkan dua angka sama adalah P(A) = .

c. Peluang mendapatkan jumlah 5 adalah P(A) = .

d. Peluang mendapatkan dua angka sama dan berjumlah 5, = …

e. Maka peluang mendapatkan dua angka sama atau berjumlah 5 adalah …

Jawaban:

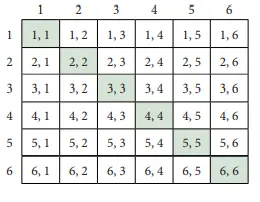
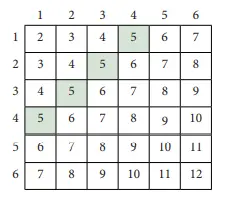
Peluang mendapatkan dua angka sama atau berjumlah 5. Dua kejadian ini saling lepas seperti dapat dilihat pada kedua tabel di atas yang menunjukkan hasil angka sama dan yang berjumlah 5. Peluang mendapatkan angka sama adalah, P(A) = 6/36. Peluang mendapatkan jumlah 5 adalah, P(B) = 4/36. Oleh karena itu, peluang mendapatkan angka yang sama atau berjumlah 5 adalah, P(A∪B) = P(A) + P(B) = 6/36 + 4/36 = 10/36

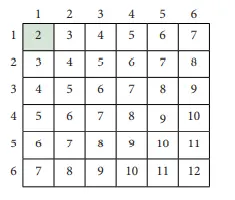
2. Tentukan peluang mendapatkan dua angka sama atau berjumlah 2.

• Apakah kedua kejadian ini saling lepas atau tidak saling lepas?

• Tentukan peluang mendapatkan dua angka sama, peluang mendapatkan jumlah 2, dan peluang mendapatkan dua angka yang sama dan berjumlah 2.

Jawaban:

Peluang mendapatkan dua angka sama atau berjumlah 2 merupakan kejadian yang tidak saling lepas, sehingga P(A∪B) = P(A) + P(B) – P(A∩B)

P(A) = 6/36, P(B) = 1/36 , P(A∩B) = 1/36 Oleh karena itu P(A∪B) = 6/36 + 1/36 – 1/36 = 6/36

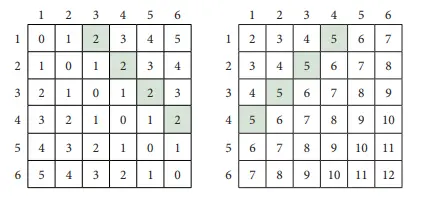
3. Tentukan peluang bahwa nilai mutlak dari selisihnya adalah 3 atau mendapatkan jumlah 5.

Jawaban:

Peluang bahwa nilai mutlak dari selisih adalah 2 atau mendapatkan jumlah 5. Kedua kejadian ini saling lepas seperti terlihat pada tabel ruang sampel di atas. Kita juga bisa bernalar bahwa pasangan bilangan yang membentuk 5 adalah 1, 4 dan 2, 3, yang mana nilai mutlak dari selisihnya bukan 2, maka peluangnya adalah, P(A∪B) = P(A) + P(B) = 8/36 + 4/36 = 12/36 = 1/3

4. Tentukan peluang bahwa nilai mutlak dari selisihnya adalah 2 atau mendapatkan jumlah 11.

Jawaban:

Peluang bahwa nilai mutlak dari selisih adalah 2 atau mendapatkan jumlah 11 adalah P(A∪B) = P(A) + P(B) = 8/36 + 2/36 = 10/36 = 2/18 karena kedua kejadian adalah saling lepas.

 

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***