ohgreat.id-Jawaban Latihan 6.6 dan Uji Kompetensi halaman 168 Fungsi Kuadrat Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMA/SMK Kelas 10 halaman 168. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMA/SMK Kelas 10 Kurikulum Merdeka Bab 6 Fungsi Kuadrat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Latihan 6.6
1. Bandingkan fungsi linier dengan fungsi kuadrat.
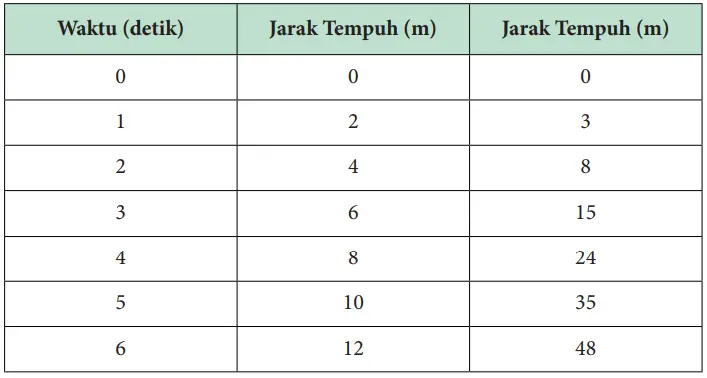
Apakah untuk setiap detik kenaikan jarak sama untuk kedua fungsi? Jelaskan.
Jawaban:
Berdasarkan data dalam tabel maka untuk fungsi linear jika waktu bertambah satu detik maka jarak bertambah 2 m sedangkan untuk fungsi kuadrat perubahan pertambahan jarak terjadi ketika waktu bertambah satu detik.
2. Tabel di bawah menunjukkan hubungan antara kelajuan mobil dengan efisiensi bahan bakar. Buatlah pendekatan grafik fungsi kuadrat dengan P (x) adalah penghematan bahan bakar dan x adalah kelajuan mobil.
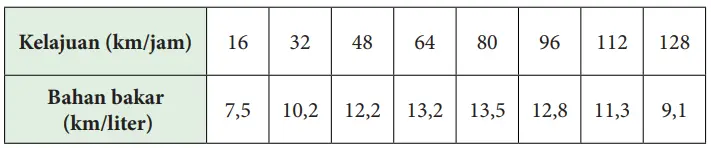
Berapa kelajuan yang menghasilkan penghematan maksimum?
Jawaban:
Fungsi kuadrat F(x) = – 00165x² + 0,251x + 3,9
Penghematan maksimum terjadi pada kelajuan 80 km/jam.
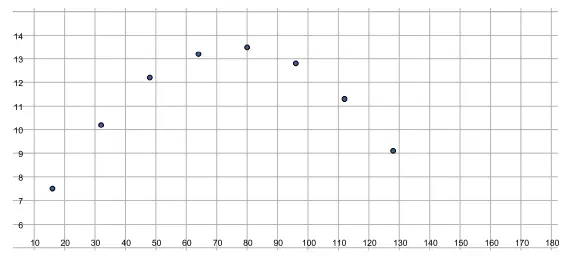
3. Bandingkan fungsi eksponen dengan fungsi kuadrat. Apakah fungsi eksponen mempunyai nilai maksimum atau nilai minimum?
Jawaban:
Fungsi eksponen tidak memiliki nilai minimum dan tidak memiliki nilai maksimum.
Uji Kompetensi
1. Dari grafik berikut, yang manakah yang merupakan grafik fungsi kuadrat?
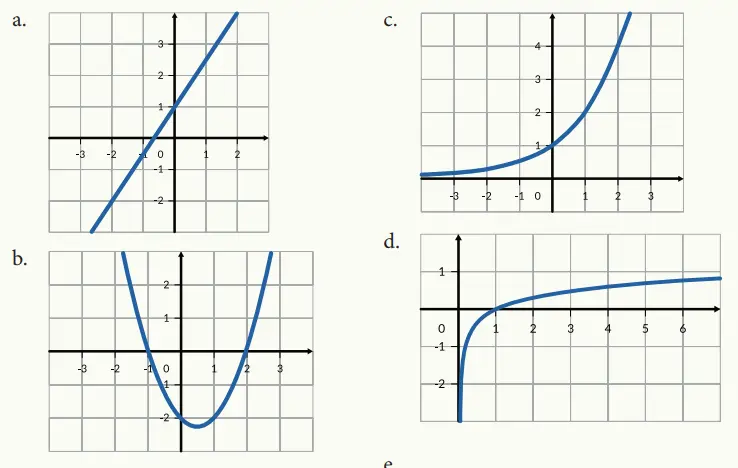
Jawaban:
Grafik b
2. Gambarkan grafik fungsi y = 2x² – 4x – 16
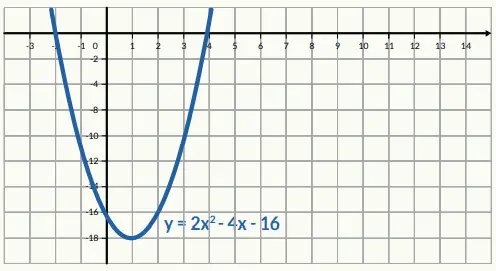
Jawaban:
a. Tentukan titik potong grafik dengan sumbu x
Jawaban:
Memotong sumbu X di (-2,0) dan (4,0)
b. Tentukan titik potong grafik dengan sumbu y
Jawaban:
Memotong sumbu Y di (0,-16)
c. Tentukan sumbu simetrinya.
Jawaban:
Sumbu simetri x = 1
d. Apakah fungsi ini memiliki nilai maksimum atau minimum? Tentukan nilainya.
Jawaban:
Nilai minimum, yaitu (1,-18)
3. Bola dilemparkan ke atas dari tanah dengan kecepatan tertentu sehingga ketinggian yang dicapai merupakan fungsi dari waktu, h(t)= -5t² + 40t Berapa ketinggian maksimum yang dicapai oleh bola?
Jawaban:
a. Alternatif 1
h(t)= -5t(t – 8)
memotong sumbu X di (0,0) dan (8,0)
Sumbu simetrinya x = 0 + 8/2 = 4
h(4)= -5(4)(4 – 8)= 80
b. Alternatif 2
D= b² – 4ac
= 40²- 4(-5)(0) = 1600
D/-4a = 1600/ (-4(-5))
= 80
4. Pendapatan dari hasil penjualan barang P(q) ditentukan oleh jumlah barang yang diproduksi q. P(q) = -20q² + 3000q . Tentukan pendapatan maksimal atau optimal dan jumlah barang yang bersesuaian dengannya.
Jawaban:
Ketinggian maksimum dapat dihitung
a. Alternatif 1
P(q) = -20q(q – 150)
Memotong sumbu X di (0,0) dan (150,0)
Sumbu simetrinya x = (0 + 150)/ 2 = 75
P(75) = -20(75) (75-150) =112.500
b. Alternatif 2
D/ (-4a) = 9000000/(-4(-20))= 112500
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
