ohgreat.id-Jawaban Latihan 5.1 Nomor 1 sampai 3 halaman 132 Sistem Persamaan Linear Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMA/SMK Kelas 10 halaman 132. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMA/SMK Kelas 10 Kurikulum Merdeka Bab 5 Sistem Persamaan dan Pertidaksamaan Linear. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Latihan 5.1
- 1.0.1 1. Asep memiliki beberapa tongkat dengan tiga jenis ukuran, ukuran a, ukuran b, dan ukuran c. Selanjutnya Asep menjajarkan 3 tongkat ukuran a, 2 tongkat ukuran b, dan 1 tongkat ukuran c dan panjangnya 390 cm. Kemudian Asep menjajarkan sebuah tongkat ukuran a, 3 tongkat ukuran b, dan 2 tongkat ukuran c dan panjangnya 460 cm. Selain itu Asep juga mengamati bahwa 2 tongkat ukuran a sama panjang dengan tongkat ukuran c.
- 1.0.1.1 a. Tuliskan pengukuran pertama ke dalam persamaan matematika.
- 1.0.1.2 b. Tuliskan hasil pengukuran kedua dan ketiga ke dalam persamaan matematika juga untuk menghasilkan sistem persamaan.
- 1.0.1.3 c. Apakah sistem persamaan itu sebuah sistem persamaan linear? Bagaimana kamu tahu?
- 1.0.1.4 d. Selesaikan sistem persamaan tersebut.
- 1.0.1.5 e. Ada berapa solusi yang ada?
- 1.0.1.6 f. Berapakah panjang tiap jenis tongkat?
- 1.0.2 2. Sebuah minuman dijual dalam tiga kemasan berbeda: kecil, sedang, dan besar. Jika Bonar membeli 3 kemasan kecil, 2 kemasan sedang, dan 3 kemasan besar, dia mendapat minuman sebanyak 4.700 ml. Apabila Bonar membeli 3 kemasan kecil, 1 kemasan sedang, dan 2 kemasan besar, dia mendapat 3.300 ml. Dan jika Bonar membeli 2 kemasan sedang dan 2 kemasan besar, dia mendapat 2.800 ml minuman. Berapakah volume tiap jenis kemasan?
- 1.0.2.1 a. Tuliskan sistem persamaan yang bersesuaian dengan permasalahan tersebut.
- 1.0.2.2 b. Apakah sistem persamaan itu termasuk sistem persamaan linear? Tuliskan alasannya.
- 1.0.2.3 c. Selesaikan sistem persamaan tersebut.
- 1.0.2.4 d. Ada berapa solusi yang ada? Jelaskan.
- 1.0.2.5 e. Apa artinya bagi Bonar jika sistem persamaan linear ini memiliki banyak solusi?
- 1.0.3 3. Bu Wati membeli tiga jenis buah. Kalau ia membeli 3 kg jeruk, 3 kg pepaya, dan 1 kg salak, ia harus membayar Rp130.000,00. Jika Bu Wati membeli 2 kg jeruk, 2 kg pepaya, dan 1 kg salak, ia harus membayar Rp100.000,00. Jika Bu Wati mau membeli 1 kg jeruk dan 1 kg pepaya, ia harus membayar Rp50.000,00. Berapakah harga tiap kg setiap jenis buah?
- 1.0.3.1 a. Tuliskan sistem persamaan yang bersesuaian dengan permasalahan tersebut.
- 1.0.3.2 b. Apakah sistem persamaan itu termasuk sistem persamaan linear? Tuliskan alasannya.
- 1.0.3.3 c. Selesaikan sistem persamaan tersebut.
- 1.0.3.4 d. Ada berapa solusi yang ada? Jelaskan.
- 1.0.3.5 e. Apa artinya bagi Bu Wati jika sistem persamaan linear ini tidak memiliki solusi?
- 1.0.4 4. Untuk setiap model matematika berikut, tentukan apakah model matematika tersebut merupakan sistem persamaan linear atau bukan. Jelaskan.
- 1.0.5 5. Pak Musa memiliki toko beras dan menjual campuran beras. Campuran 2 kg beras A, 2 kg beras B, dan 1 kg beras C dihargai Rp50.000,00. Dan campuran 4 kg beras A, 2 kg beras B, dan 3 kg beras C dihargai Rp91.000,00. Selanjutnya campuran 4 kg beras A, 4 kg beras B, dan 2 kg beras C dihargai Rp95.000,00. Tentukan harga tiap kg beras A, beras B, dan beras C.
- 1.0.6 6. Maria adalah penjaga tiket di sirkus. Ada tiga jenis tiket yang dijual. Keluarga Andi membeli 4 tiket anak-anak, 2 tiket dewasa, dan 1 tiket lansia dan membayar Rp640.000,00. Dan keluarga Butet membeli 1 tiket anak-anak, 3 tiket dewasa, dan 2 tiket lansia dan membayar Rp550.000,00. Selanjutnya keluarga Danu membeli 3 tiket anak-anak, 1 tiket dewasa, dan 1 tiket lansia dan membayar Rp450.000,00. Berapakah harga setiap jenis tiket yang dijual Maria?
- 1.0.7 7. Kinan menimbang bola yang ada di lemari sekolah. Pada penimbangan pertama, Kinan menimbang dua bola basket, sebuah bola kaki, dan tiga bola voli dan hasilnya 2.500 g. Penimbangan kedua, sebuah bola basket, dua buah bola kaki, dan dua buah bola voli beratnya 2.050 g. Selanjutnya penimbangan ketiga, dua buah bola basket dan sebuah bola voli beratnya 1.550 g. Berapa berat tiap jenis bola?
- 1.0.8 8. Butet ingin membeli buah. Semua buah yang ada sudah dikemas menjadi paket. Paket A terdiri atas 5 jeruk, 1 mangga, dan 8 salak beratnya 1,5 kg. Dan paket B terdiri atas 10 jeruk, 2 mangga, dan 4 salak beratnya 2 kg. Selanjutnya paket C terdiri atas 3 mangga, dan 12 salak beratnya 2 kg. Jika setiap jenis buah itu identik, berapakah berat masing-masing jenis buah?
- 1.0.1 1. Asep memiliki beberapa tongkat dengan tiga jenis ukuran, ukuran a, ukuran b, dan ukuran c. Selanjutnya Asep menjajarkan 3 tongkat ukuran a, 2 tongkat ukuran b, dan 1 tongkat ukuran c dan panjangnya 390 cm. Kemudian Asep menjajarkan sebuah tongkat ukuran a, 3 tongkat ukuran b, dan 2 tongkat ukuran c dan panjangnya 460 cm. Selain itu Asep juga mengamati bahwa 2 tongkat ukuran a sama panjang dengan tongkat ukuran c.
Latihan 5.1
1. Asep memiliki beberapa tongkat dengan tiga jenis ukuran, ukuran a, ukuran b, dan ukuran c. Selanjutnya Asep menjajarkan 3 tongkat ukuran a, 2 tongkat ukuran b, dan 1 tongkat ukuran c dan panjangnya 390 cm. Kemudian Asep menjajarkan sebuah tongkat ukuran a, 3 tongkat ukuran b, dan 2 tongkat ukuran c dan panjangnya 460 cm. Selain itu Asep juga mengamati bahwa 2 tongkat ukuran a sama panjang dengan tongkat ukuran c.
a. Tuliskan pengukuran pertama ke dalam persamaan matematika.
Jawaban:
a. 3a + 2b + c = 390
b. Tuliskan hasil pengukuran kedua dan ketiga ke dalam persamaan matematika juga untuk menghasilkan sistem persamaan.
Jawaban:
3a + 2b + c = 390
a + 3b + 2c = 460
2a – c = 0
c. Apakah sistem persamaan itu sebuah sistem persamaan linear? Bagaimana kamu tahu?
Jawaban:
Sistem persamaan linear, 3 persamaan dengan 3 variabel yang semua variabelnya berpangkat 1.

d. Selesaikan sistem persamaan tersebut.
Jawaban:
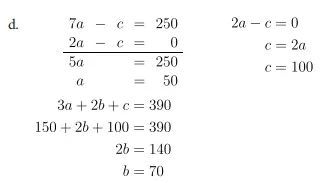
e. Ada berapa solusi yang ada?
Jawaban:
Ada 1 (set) solusi yaitu a = 50, b = 70, c = 100
f. Berapakah panjang tiap jenis tongkat?
Jawaban:
Tongkat a panjangnya 50 cm, tongkat b panjangnya 70 cm, tongkat cpanjangnya 100 cm.
2. Sebuah minuman dijual dalam tiga kemasan berbeda: kecil, sedang, dan besar. Jika Bonar membeli 3 kemasan kecil, 2 kemasan sedang, dan 3 kemasan besar, dia mendapat minuman sebanyak 4.700 ml. Apabila Bonar membeli 3 kemasan kecil, 1 kemasan sedang, dan 2 kemasan besar, dia mendapat 3.300 ml. Dan jika Bonar membeli 2 kemasan sedang dan 2 kemasan besar, dia mendapat 2.800 ml minuman. Berapakah volume tiap jenis kemasan?
a. Tuliskan sistem persamaan yang bersesuaian dengan permasalahan tersebut.
Jawaban:
Jika digunakan variabel k volume kemasan kecil, s volume kemasan sedang, dan b volume kemasan besar (semua volume dalam ml).
Sistem persamaannya
3k + 2s + 3b = 4700
3k + s + 2b = 3300
2s + 2b = 2800
b. Apakah sistem persamaan itu termasuk sistem persamaan linear? Tuliskan alasannya.
Jawaban:
Semua variabel pada sistem persamaan tersebut berpangkat satu, maka sistem persamaan tersebut adalah sistem persamaan linear.
c. Selesaikan sistem persamaan tersebut.
Jawaban:
Eliminasi persamaan pertama dan persamaan kedua.
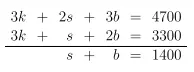
Persamaan yang dihasilkan adalah persamaan yang sama dengan persamaan ketiga dalam sistem persamaan linear (seluruh persamaan dikalikan 2).
d. Ada berapa solusi yang ada? Jelaskan.
Jawaban:
Proses pada (c) menghasilkan persamaan yang sama dengan persamaan ketiga (grafiknya berupa dua garis berimpit), maka sistem persamaan linear ini memiliki banyak solusi.
e. Apa artinya bagi Bonar jika sistem persamaan linear ini memiliki banyak solusi?
Jawaban:
Ada banyak kemungkinan volume kemasan kecil, sedang, dan besar, contohnya k = 366, 66, s = 600, b = 800 adalah solusi, k = 333, 33, s = 500, b = 900 juga solusi.
3. Bu Wati membeli tiga jenis buah. Kalau ia membeli 3 kg jeruk, 3 kg pepaya, dan 1 kg salak, ia harus membayar Rp130.000,00. Jika Bu Wati membeli 2 kg jeruk, 2 kg pepaya, dan 1 kg salak, ia harus membayar Rp100.000,00. Jika Bu Wati mau membeli 1 kg jeruk dan 1 kg pepaya, ia harus membayar Rp50.000,00. Berapakah harga tiap kg setiap jenis buah?
a. Tuliskan sistem persamaan yang bersesuaian dengan permasalahan tersebut.
Jawaban:
Jika j adalah harga tiap kg jeruk, p adalah harga tiap kg pepaya, dan s adalah harga tiap kg salak (semua harga dalam ribu rupiah), maka sistem persamaannya adalah:
3j + 3p + s = 130
2j + 2p + s = 100
j + p = 50
b. Apakah sistem persamaan itu termasuk sistem persamaan linear? Tuliskan alasannya.
Jawaban:
Sistem persamaan linear karena semua variabelnya berpangkat satu.
c. Selesaikan sistem persamaan tersebut.
Jawaban:
Eliminasi persamaan pertama dan kedua diperoleh:
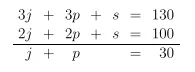
Bandingkan persamaan ini dengan persamaan ketiga.
d. Ada berapa solusi yang ada? Jelaskan.
Jawaban:
Grafiknya berupa dua garis yang sejajar, maka sistem persamaan linear ini adalah sistem persamaan linear yang tidak memiliki solusi.
e. Apa artinya bagi Bu Wati jika sistem persamaan linear ini tidak memiliki solusi?
Jawaban:
Harga buah-buahan di setiap paket berbeda-beda.
4. Untuk setiap model matematika berikut, tentukan apakah model matematika tersebut merupakan sistem persamaan linear atau bukan. Jelaskan.
a. 5x – 3y = 10
y = x² – 5x + 6
b. 3x – 5y + z = 10
x² + y² + z²= 8
c. 5x – 3y + 2z = 20
3x + 4y – z = 15
2x – 5y – 3z = 10
d. 15x – 23y + 2z = 200
31x + 42y – 1/z= 150
23x – 45y – 33z= 100
e. x – 3y + 2z = 20
2x + y – 3z = 15
3x – 2y – z = 35
Jawaban:
a. Bukan sistem persamaan linear, ada variabel x²
b. Bukan sistem persamaan linear, ada variabel x², y², z²
c. Sistem Persamaan Linear, semua variabel berpangkat 1.
d. Bukan Sistem Persamaan Linear, ada variabel 1/z
e. Sistem Persamaan Linear, semua variabel berpangkat 1.
5. Pak Musa memiliki toko beras dan menjual campuran beras. Campuran 2 kg beras A, 2 kg beras B, dan 1 kg beras C dihargai Rp50.000,00. Dan campuran 4 kg beras A, 2 kg beras B, dan 3 kg beras C dihargai Rp91.000,00. Selanjutnya campuran 4 kg beras A, 4 kg beras B, dan 2 kg beras C dihargai Rp95.000,00. Tentukan harga tiap kg beras A, beras B, dan beras C.
a. Tuliskan model matematikanya.
Jawaban:
Jika a adalah harga 1 kg beras A, b harga 1 kg beras B, dan c adalah harga 1 kg beras C,
maka
2a + 2b + c = 50
4a + 2b + 3c= 91
4a + 4b + 2c= 95
b. Apakah model matematika itu merupakan sistem persamaan linear?
Jawaban:
Sistem persamaan linear karena semua variabelnya berpangkat satu.
c. Ada berapa solusi yang dimiliki oleh sistem ini? Bagaimana kalian tahu?
Jawaban:
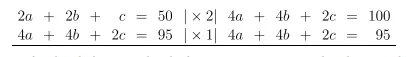
6. Maria adalah penjaga tiket di sirkus. Ada tiga jenis tiket yang dijual. Keluarga Andi membeli 4 tiket anak-anak, 2 tiket dewasa, dan 1 tiket lansia dan membayar Rp640.000,00. Dan keluarga Butet membeli 1 tiket anak-anak, 3 tiket dewasa, dan 2 tiket lansia dan membayar Rp550.000,00. Selanjutnya keluarga Danu membeli 3 tiket anak-anak, 1 tiket dewasa, dan 1 tiket lansia dan membayar Rp450.000,00. Berapakah harga setiap jenis tiket yang dijual Maria?
Jawaban:
Jika a menyatakan harga tiket anak, d menyatakan harga tiket dewasa, dan l harga tiket lansia (semuanya dalam ribu rupiah), maka sistem persamaannya menjadi:
4a + 2d + l = 640
a + 3d + 2l= 550
3a + d + l + 450
Ini adalah sistem persamaan linear yang solusinya a = 90, d = 100, l= 80 . Harga tiket anak-anak adalah Rp90.000,00, harga tiket dewasa adalah Rp100.000,00, dan harga tiket lansia adalah Rp80.000,00.
7. Kinan menimbang bola yang ada di lemari sekolah. Pada penimbangan pertama, Kinan menimbang dua bola basket, sebuah bola kaki, dan tiga bola voli dan hasilnya 2.500 g. Penimbangan kedua, sebuah bola basket, dua buah bola kaki, dan dua buah bola voli beratnya 2.050 g. Selanjutnya penimbangan ketiga, dua buah bola basket dan sebuah bola voli beratnya 1.550 g. Berapa berat tiap jenis bola?

Jawaban:
Jika b menyatakan berat sebuah bola basket, k berat sebuah bola kaki, dan v berat sebuah bola voli, maka model matematikanya adalah sistem persamaan linear
2b + k + 3v = 2500
b + 2k + 2v = 2050
2b + v = 1550
yang solusinya adalah b = 650, k = 450, v= 250
8. Butet ingin membeli buah. Semua buah yang ada sudah dikemas menjadi paket. Paket A terdiri atas 5 jeruk, 1 mangga, dan 8 salak beratnya 1,5 kg. Dan paket B terdiri atas 10 jeruk, 2 mangga, dan 4 salak beratnya 2 kg. Selanjutnya paket C terdiri atas 3 mangga, dan 12 salak beratnya 2 kg. Jika setiap jenis buah itu identik, berapakah berat masing-masing jenis buah?
Jawaban:
Jika j untuk menyatakan berat sebuah jeruk, m untuk menyatakan berat sebuah mangga, dan s untuk menyatakan berat sebuah salak maka masalah tersebut dapat dimodelkan ke dalam sistem persamaan linear berikut.
m + 5j + 8s = 1,5
2m+ 10j+ 4s = 2
3m + 12s= 2
yang solusinya adalah j = 1/10, m = 1/3 , s = 1/12
Solusi yang didapatkan perlu dikembalikan ke permasalahan nyata. Sesuai definisi setiap variabel, sebuah jeruk beratnya 0,1 kg, sebuah mangga beratnya 1/3 kg, dan setiap salak beratnya 1/12 kg.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
