ohgreat.id-Jawaban Latihan 4.6 dan Latihan 4.7 halaman 118 Perbandingan Trigonometri Matematika SMA/SMK Kelas 10 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMA/SMK Kelas 10 halaman 118. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMA/SMK Kelas 10 Kurikulum Merdeka Bab 4 Perbandingan Trigonometri. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Latihan 4.6

1. Sebuah segitiga siku-siku sama kaki memiliki panjang dua sisinya 8cm. Berapa panjang sisi miringnya?

Jawaban:

misal sisi tegak lurus adalah a dan b = 8 cm, sisi miring adalah c

√a2 + b2 = √c

√82 + 82 = √c

√64 + 64 = √c

√128 = √c

√64 . √2 = √c

c = 8√2

Jadi Sisi miring adalah c = 8√2

2. Sebuah segitiga siku-siku mempunyai sudut 30ºdan 60º.

a. Tuliskan panjang setiap sisi segitiganya yang memungkinkan.

Jawaban:

Contoh jawaban yang tepat: 6 cm, 3 cm, 3√3 cm

b. Nia berkata segitiga ini memiliki panjang sisi seperti berikut: 5√3 cm, 5 cm, dan 15 cm. Menurut kalian, apakah panjang sisi yang dikemukakan Nia memungkinkan? Jelaskan mengapa.

Jawaban:

Tidak mungkin. Perbandingan salah satu sisi segitiga dengan sisi miringnya harus setengahnya, sedangkan 5 cm bukan setengah dari 15 cm

Latihan 4.7

Soal Pemahaman

1. Cari panjang sisi x dan z !

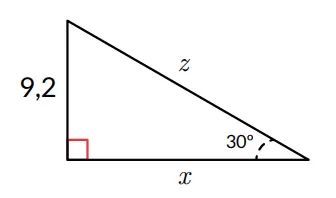
Jawaban:

z = 18,4 dan x = 15,94

2. Segitiga ABC memiliki panjang sisi sebagai berikut:

Sisi AC = 5   Sisi CB = 12     Sisi AB = 13

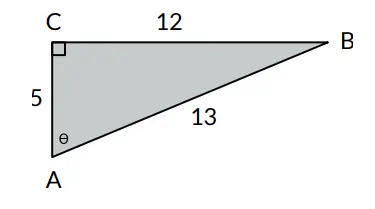
a. Tentukan nama setiap sisi segitiga siku-siku berikut.

b. Cari hasil sin θ!

c. Cari hasil cos θ!

Jawaban:

a. Sisi depan = sisi CB, sisi samping = sisi CA, sisi miring = sisi AB

b. sin θ = 12/13

c. cos θ = 5/13

Soal Aplikasi

3. KLM adalah segitiga dengan besar sudut dan panjang seperti pada gambar di samping. KLM adalah segitiga dengan besar sudut dan panjang seperti pada Gambar di samping.

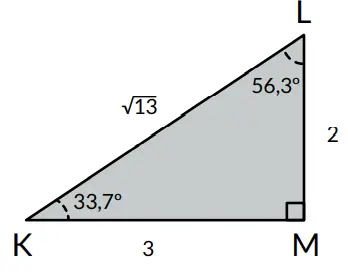
a. Tentukan hasil perbandingan trigonometri berdasarkan sudut yang ditentukan.

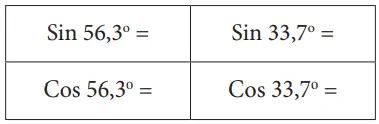
Jawaban:

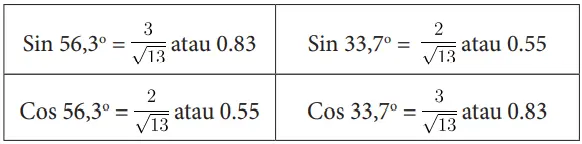
b. Dua pasang nilai perbandingan trigonometri yang mana yang hasilnya sama? Mengapa demikian?

Jawaban:

Sin 56,3o sama dengan cos 33,7o. Kemudian, sin 33,7o sama dengan cos 56,3o. Hal ini terjadi karena kedua sudut lancip pada segitiga siku-siku terletak berseberangan sehingga sisi depan salah satu sudut lancipnya sama dengan sisi samping sudut lancip yang satunya.

4. Cari panjang x, y, dan z !

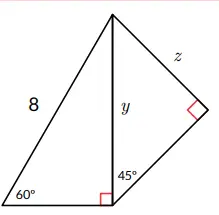
Jawaban:

x = 4, y = 4√3 , dan z = 2√6

5. Dari jarak 120m, seorang pengukur tanah menemukan sudut yang terbentuk antara garis permukaan dan puncak gedung adalah 30º. Gunakan perbandingan trigonometri untuk mencari tinggi gedung tersebut! Cari hasilnya dengan membulatkan ke satuan meter terdekat.

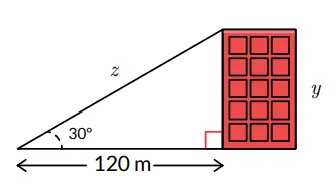
Jawaban:

Tinggi gedung = 40√3

Soal Penalaran

6. Terdapat susunan beberapa segitiga siku-siku seperti berikut.

a. Desi berkata, ia perlu mencari sin 30o untuk mencari panjangnya x. Apakah kamu setuju dengan Desi?

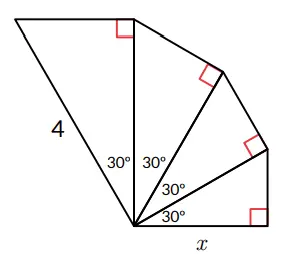
Jawaban:

Saya tidak setuju. Mencari sin 30º tidak akan menolong Desi untuk menemukan panjang x. Panjang sisi yang perlu diketahui adalah sisi samping 30º, maka yang lebih bermanfaat adalah mencari cos 30º.

b. Cari panjang x !

Jawaban:

x = 1

7. Gambar persegi panjang dengan panjang diagonal dua kali dari lebarnya. Buat persamaan untuk mencari panjang persegi panjang tersebut!

Jawaban:

Pada dasarnya siswa harus menggambar dua segitiga siku-siku yang membentuk persegi dengan dua sudut lancip istimewa yaitu 30º dan 60º.

Dengan merujuk ke tabel sudut istimewa perbandingan trigonometri, persamaan untuk mencari panjang persegi panjang adalah Lebar persegi dibagi dengan½√3

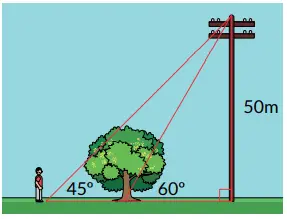
8. Seorang laki-laki sedang berjalan di sebuah area hijau. Ia berpapasan dengan sebatang pohon dan sebuah tiang listrik. Jika tinggi tiang 50 meter dengan sudut antara laki-laki dan puncak tiang 45º dan sudut antara pohon dengan puncak tiang 60º, berapa jarak antara seorang laki-laki tersebut dan pohon?

Jawaban:

Dua nilai yang harus dicari siswa adalah jarak antara laki-laki dan tiang serta jarak antara pohon dan tiang. Kemudian, siswa dapat melakukan operasi pengurangan untuk menemukan jarak antara laki-laki dan pohon. Jarak antara laki-laki dengan tiang adalah 50 m (karena tan 45º = 1).Jarak antara pohon dan tiang dapat dicari dengan menggunakan nilai perbandingan trigonometri tan 60º.

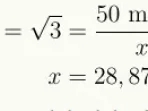
Jarak antara laki-laki dan pohon = 50 meter – 28,87 meter = 21,13 meter.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***