ohgreat.id-Jawaban Konvers dan Cermati halaman 142 Segitiga Sama Kaki Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 142. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Segitiga Sama Kaki
Segitiga Sama Kaki
Konvers
Q. Teorema-teorema berikut telah kita buktikan sebelumnya. Tentukan secara berturut-turut yang diketahui dan yang disimpulkan.
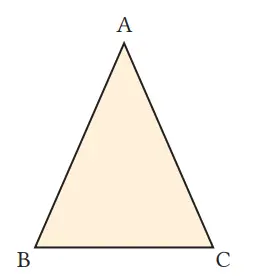
(1) Dua sudut alas dari segitiga sama kaki besarnya sama.
Jawaban:
⟨Asumsi⟩ AB = AC
⟨Kesimpulan⟩ ∠B = ∠C
(2) Segitiga yang memiliki dua sudut yang sama besar adalah segitiga sama kaki.
Jawaban:
⟨Asumsi⟩ ∠B = ∠C
⟨Kesimpulan⟩ AB = AC
Ketika kita susun ulang teorema-teorema di atas, pada ∆ABC,
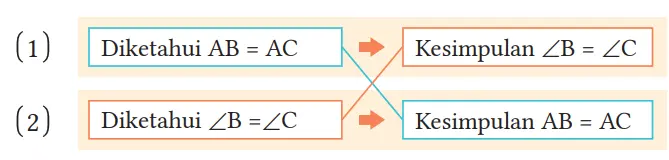
Jika yang diketahui dan yang disimpulkan pada dua pernyataan memiliki letak yang berkebalikan, kita sebut pernyataan-pernyataan tersebut saling konvers. Sebagai contoh (2) adalah konvers dari (1), dan (1) adalah konvers dari (2).
Soal 6
Tentukan konvers dari pernyataan-pernyataan berikut. Periksa apakah pernyataan-pernyataan tersebut benar atau tidak.
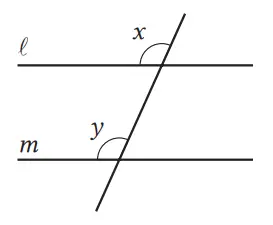
(1) Jika garis ℓ dan m sejajar, maka sudut-sudut yang berkorespondensi (bersesuaian) sama besar.
Jawaban:
Konvers-nya adalah “Jika ∠x dan ∠y sama besar, maka garis l dan m adalah sejajar”. Konvers tersebut bernilai Benar
(2) Jika a > 0 dan b > 0, maka ab > 0.
Jawaban:
Konvers-nya adalah “Jika ab > 0, maka a > 0 dan b > 0”. Konvers tersebut bernilai Salah.
(3) Pada ∆ABC, jika ∠A = 90°, maka ∠B + ∠C = 90°.
Jawaban:
Konvers-nya adalah “Pada ΔABC, jika ∠B + ∠C = 90°, maka ∠A = 90°”. Konvers tersebut bernilai Benar.
Memberikan Contoh Penyangkal membahas Soal 6 (2).
Proposisi matematika memiliki prasyarat “segala sesuatu tentang ~”. Sebenarnya, kalimat yang ditampilkan di Soal 6 (2) adalah “Untuk semua bilangan real a dan b, jika ab > 0, maka a > 0 dan b > 0”.
Oleh karena itu, untuk menunjukkan bahwa proposisi ini salah, cukup memberikan satu contoh yang tidak berlaku (Contoh penyangkal). Peserta didik diharapkan memperhatikan bahwa di dalam Buku Siswa menggunakan kata “setiap”.
Berikut ini adalah contoh proposisi di mana kebalikannya tidak benar.
a. Jika dua bilangan bulat a dan b sama-sama genap, maka ab juga genap.
b. Jika x = 3, maka x2 = 9.
c. Grafik perbandingan senilai berbentuk garis.
d. Segitiga sama sisi memiliki satu garis simetris.
e. Kedua diagonal belah ketupat berpotongan tegak lurus.
Seperti telah diselidiki di Soal 6, jika suatu pernyataan benar, maka konvers-nya tidak selalu benar. Dengan demikian, untuk memeriksa apakah konvers dari suatu teorema itu benar, kita harus membuktikannya.
Selain itu, untuk menunjukkan bahwa suatu pernyataan itu tidak benar, maka kita perlu memberi contoh penyangkal.
Cermati
Memberi Contoh Penyangkal
Untuk membuktikan bahwa pernyataan berikut tidak benar untuk semua kasus, cukup dengan memberi contoh.
“Jika ab > 0, maka a > 0, b > 0.”
〈Contoh untuk menunjukkan bahwa pernyataan salah〉 a = –2, b = –3
Pernyataan di atas secara lengkap berbunyi, “Untuk sebarang bilangan a dan b, jika ab > 0, maka selalu diperoleh a > 0 dan b > 0.”
Jadi, jika kita berikan suatu contoh yang menunjukkan pernyataan tidak benar, maka kita sudah menunjukkan bahwa pernyataan tersebut tidak benar. Memberi contoh yang mengakibatkan suatu pernyataan tidak benar disebut “memberi contoh penyangkal”.
Tentukan konvers dari tiap pernyataan berikut. Tunjukkan bahwa konversnya tidak benar dengan memberi contoh penyangkal.
(1) Jika a > 0, b > 0, maka a + b > 0.
Jawaban:
Jika a + b > 0, maka a > 0 dan b > 0.
(Contoh penyangkal) a = 3, b = –2
(2) Jika ∆ABC ≅ ∆DEF, maka luas ∆ABC dan ∆DEF sama besar.
Jawaban:
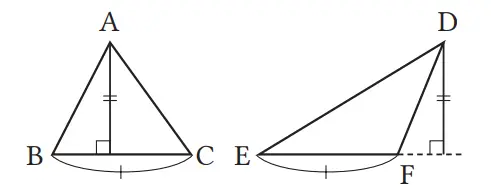
Jika luas ΔABC dan ΔDEF sama, maka ΔABC ≅ ΔDEF.
(Contoh penyangkal)
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
