ohgreat.id-Jawaban Jajargenjang Khusus halaman 157 Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 157. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Segi Empat

Jajargenjang Khusus

Q. Pada segi empat dalam tabel berikut, tulis O bila memenuhi sifat yang ditunjukkan di sebelah kiri, dan tulis X bila tidak memenuhi.

Jawaban:

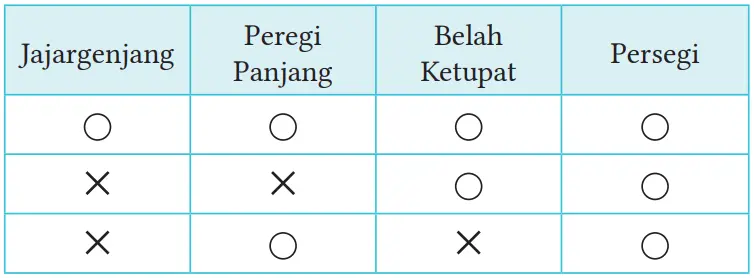
Persegi panjang, belah ketupat, dan persegi didefinisikan sebagai berikut.

a. Segi empat yang semua sudutnya sama besar disebut persegi panjang.

b. Segi empat yang semua sisinya sama panjang disebut belah ketupat.

c. Segi empat yang semua sudutnya sama besar dan semua sisinya sama panjang disebut persegi.

Definisi persegi panjang, yaitu “segi empat yang semua sudutnya sama besar” memenuhi syarat sebagai jajargenjang, yakni “dua pasang sisi berhadapan masing-masing sama besar”. Dengan demikian, kita dapat menyatakan bahwa persegi panjang adalah jajargenjang.

Soal 1

Dapatkah kita menyatakan bahwa belah ketupat merupakan jajargenjang? Jelaskan!

Jawaban:

Dapat dikatakan sebagai Jajargenjang.

⟨Alasan⟩

Definisi belah ketupat adalah “segi empat yang memiliki 4 sisi dengan panjang yang sama”, maka memenuhi persyaratan untuk menjadi jajargenjang, yaitu “dua pasang sisi berhadapan panjangnya masing-masing sama”.

Persegi panjang dan belah ketupat merupakan kasus khusus dari jajargenjang. Karena itu, baik persegi panjang maupun belah ketupat memiliki semua sifat jajargenjang.

Persegi adalah kasus khusus dari persegi panjang ataupun belah ketupat. Oleh karena itu, persegi memiliki semua sifat yang dimiliki persegi panjang ataupun belah ketupat.

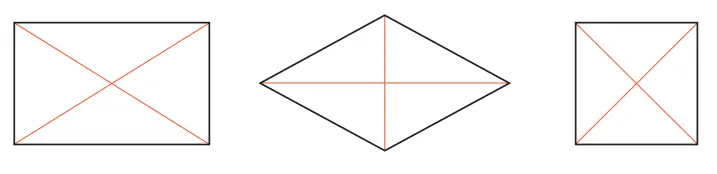
Q. Mari kita diskusikan sifat-sifat dari diagonal persegi panjang, belah ketupat, dan persegi.

Jawaban:

a. Persegi panjang: Kedua diagonal memiliki panjang yang sama dan berpotongan di titik tengah kedua diagonal.

b. Belah ketupat: Dua diagonal berpotongan secara tegak lurus di titik tengah kedua diagonal.

c. Persegi: Panjang kedua diagonal sama dan berpotongan tegak lurus di titik tengah kedua diagonalnya.

Contoh 1

Pada persegi panjang ABCD, buktikan bahwa panjang kedua diagonalnya, yaitu AC dan DB, sama panjang.

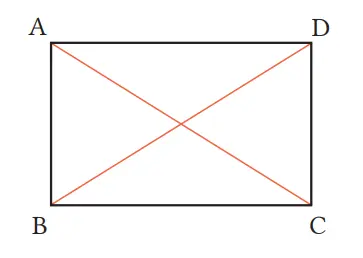
Bukti

Pada ∆ABC dan ∆DCB,diketahui bahwa ∠ABC = ∠DCB ①

Sisi berhadapan persegi panjang adalah sama panjang, maka AB = DC ②

BC adalah sisi persekutuan ③

Dari ①, ②, dan ③, berdasarkan aturan kekongruenan Sisi-Sudut-Sisi,maka ∆ABC ≅ ∆DCB

Dengan demikian, AC = DB.

Dari sifat diagonal persegi panjang, bila kita misalkan M adalah titik tengah hipotenusa BC dari segitiga siku-siku ABC seperti pada gambar berikut, maka kita dapat lihat bahwa AM = BM = CM.

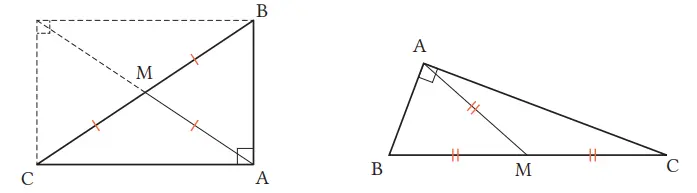
Soal 2

Pada belah ketupat ABCD, buktikan bahwa kedua diagonalnya, yaitu AC dan BD saling berpotongan tegak lurus. Misalkan O adalah titik potong antara AC dan BD.

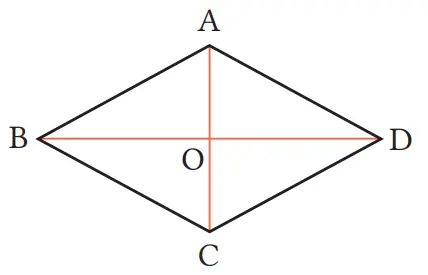
Jawaban:

Dalam ΔABO dan ΔADO, dari asumsi, sisi belah ketupat yang berdekatan adalah sama, maka AB = AD ①

Karena dua garis diagonal belah ketupat berpotongan di titik tengahnya, BO = DO ②

Juga, AO sisi persekutuan ③

Dari ①, ②, dan ③, menurut aturan kekongruenan sisi-sisi-sisi, maka ΔABO ≅ ΔADO

Oleh karena itu, ∠AOB = ∠AOD ④

Di sisi lain, ∠AOB + ∠AOD = 180° ⑤

Dari ④ dan ⑤, ∠AOB = 90°

Oleh karena itu, AC ⊥ BD.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***