ohgreat.id-Jawaban halaman 32 Sistem Persamaan dan Penyelesaiannya Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 30. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 2 Sistem Persamaan Linear Dua Variabel. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Sistem Persamaan dan Penyelesaiannya
- 1.0.1 Q. Di wahana taman hiburan, misalkan Heru melakukan permainan A dengan 2 tiket sebanyak x kali, dan permainan B dengan 1 tiket sebanyak y kali. Nyatakan jumlah total tiket yang digunakan Heru dalam sebuah persamaan.
- 1.0.2 Soal 1
- 1.0.3 Dari di halaman 32, Heru menaiki permainan sebanyak 7 kali. Kita dapat menyatakan hubungan antara x dan y dalam bentuk berikut.
- 1.0.4 Soal 2
- 1.0.5 Soal 3
- 1.0.6 Soal 4
Sistem Persamaan dan Penyelesaiannya
Q. Di wahana taman hiburan, misalkan Heru melakukan permainan A dengan 2 tiket sebanyak x kali, dan permainan B dengan 1 tiket sebanyak y kali. Nyatakan jumlah total tiket yang digunakan Heru dalam sebuah persamaan.
Jawaban:
(2x + y) lembar
Pada , jika total banyaknya tiket yang digunakan adalah 11, hubungan antara x dan y dapat dinyatakan dengan persamaan berikut.
2x + y = 11 (1)
Catatan Huruf x dan y dapat kita ganti dengan berbagai nilai bilangan. Oleh karena itu, keduanya disebut sebagai variabel.
Soal 1
Isilah tabel berikut dengan nilai y yang tepat sehingga persamaan 1 menjadi benar.
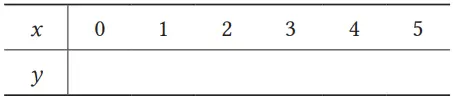
Jawaban:

Penjelasan:
Persamaan linear seperti 2x + y = 11, disebut persamaan linear dua variabel. Persamaan seperti 3x + 5 = 8, disebut persamaan linear satu variabel.
Nilai x dan y yang membuat sebuah persamaan linear dua variabel menjadi pernyataan yang benar disebut penyelesaian. Pada tabel di Soal 1,
x = 0 , y = 11 | x = 1 , y = 9 | x = 2 , y = 7
Semua nilai x dan y yang bersesuaian di atas merupakan penyelesaian dari persamaan 2x + y = 11.
Catatan: x = 0 , y = 11 dapat juga kita tulis dengan x = 0, y =11 atau (x, y) = (0, 11)
Dari di halaman 32, Heru menaiki permainan sebanyak 7 kali. Kita dapat menyatakan hubungan antara x dan y dalam bentuk berikut.
x + y = 7 (2)
Soal 2
Isilah tabel berikut dengan menyelesaikan persamaan (2).

Jawaban:
x + y = 7
x = 0 , y = 7 | x = 1 y = 6 | x = 2 y = 5 dst.

Soal 3
Dari tabel Soal 1 di halaman 32 dan tabel Soal 2 di atas, carilah nilai dari x dan y sehingga persamaan 1 dan 2 menjadi pernyataan yang benar.
Jawaban:
x = 4
y = 3
Sepasang persamaan linear dua variabel disebut sistem persamaan linear dua variabel (SPLDV). Berikut ini adalah contoh SPLDV.
2x + y = 11 (1)
x + y = 7 (2)
Dalam sistem persamaan, nilai x dan y yang membuat kedua persamaan menjadi pernyataan yang benar disebut penyelesaian dari sistem persamaan, kegiatan menemukan penyelesaiannya adalah menyelesaikan sistem persamaan.

Penyelesaian dari sistem persamaan di atas adalah
x = 4
y = 3
Soal 4
Manakah berikut ini yang merupakan penyelesaian dari sistem persamaan
2x + y = 16
x + y = 9
a. x = 5 , y = 4 | b. x = 7 , y = 2 | c. x = 9 , y = -2
Jawaban:
(b) x = 7 , y = 2
Dengan menggantikan nilai x dan y ke setiap persamaan, peserta didik dapat memeriksa apakah itu adalah penyelesaian atau bukan. Selanjutnya, (a) dan (c) masing-masing merupakan penyelesaian dari salah satu persamaan.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
