ohgreat.id-Jawaban Cara Menemukan Persamaan Garis halaman 74 Bab 3 Fungsi Linear Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 74. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 3 Fungsi Linear. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
- 1 Bagaimana Cara Menemukan Persamaan Garis
- 1.0.1 Q. Kecepatan suara di udara berubah karena perubahan suhu. Misalkan kecepatan suara adalah y m/detik ketika suhu udara x°C. Grafik di sebelah kanan menyatakan hubungan antara x dan y.
- 1.0.1.1 (1) Bacalah kecepatan suara ketika suhu udara sebesar 0°C.
- 1.0.1.2 (2) Bagaimana kecepatan suara berubah ketika suhu udara meningkat 5°C? Apa yang terjadi jika suhu meningkat 1°C?
- 1.0.1.3 (3) Diskusikan jenis persamaan yang akan terbentuk jika kita menyatakan y dalam xmenggunakan sebuah persamaan x dan y.
- 1.0.2 Penggunaan Q
- 1.0.1 Q. Kecepatan suara di udara berubah karena perubahan suhu. Misalkan kecepatan suara adalah y m/detik ketika suhu udara x°C. Grafik di sebelah kanan menyatakan hubungan antara x dan y.
- 1.1 Contoh 1
- 1.2 Contoh 2
- 1.3 Contoh 3
Bagaimana Cara Menemukan Persamaan Garis
Q. Kecepatan suara di udara berubah karena perubahan suhu. Misalkan kecepatan suara adalah y m/detik ketika suhu udara x°C. Grafik di sebelah kanan menyatakan hubungan antara x dan y.
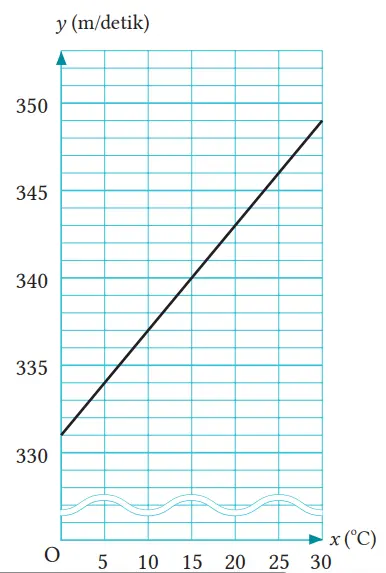
(1) Bacalah kecepatan suara ketika suhu udara sebesar 0°C.
Jawaban:
331 m/detik
(2) Bagaimana kecepatan suara berubah ketika suhu udara meningkat 5°C? Apa yang terjadi jika suhu meningkat 1°C?
Jawaban:
Jika suhu meningkat 5ºC, maka kecepatan suara bertambah 3 m/detik. Jika suhu meningkat 1ºC, maka kecepatan suara bertambah 0,6 m/detik.
(3) Diskusikan jenis persamaan yang akan terbentuk jika kita menyatakan y dalam xmenggunakan sebuah persamaan x dan y.
Jawaban:
y = 0,6x + 331
Penggunaan Q
Dengan menentukan kemiringan dan intersep y dari grafik, peserta didik menemukan bahwa fungsi linear dapat diperoleh. Berikut adalah contoh untuk memahami hal ini.
(1) Menentukan intersep y dari grafik.
(2) Dari grafik dapat dilihat bahwa kecepatan suara meningkat 3 m/detik ketika suhu naik 5ºC.
Berdasarkan hal ini, tentukan perubahan kecepatan suara saat suhu naik 1oC. Inilah yang disebut tingkat perubahan fungsi linear, yaitu kemiringan grafik. Setelah itu, peserta didik dapat menggunakan persamaan yang diperoleh di (3) untuk memprediksi kecepatan suara saat suhu 35°C, –5°C, dan lain-lain.
Contoh 1
Carilah persamaan dari fungsi linear yang gambar grafiknya berupa garis seperti berikut.
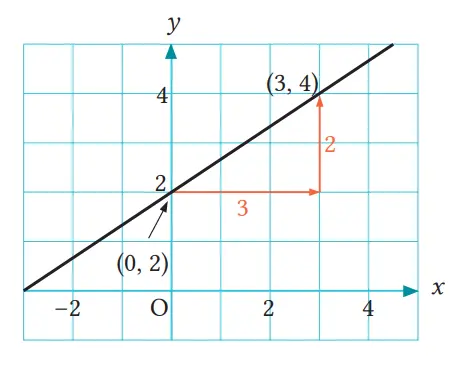
Cara
Misalkan persamaannya y = ax + b. Temukan nilai kemiringan a dan intersep b dari grafik.
Penyelesaian
Misalkan persamaan y = ax + b.
Karena grafik melalui titik (0, 2), maka b = 2
Juga dari grafik, jika kita bergerak 3 satuan ke kanan dan 2 satuan ke atas, maka a = 2/3
Oleh karena itu, persamaan dari fungsi linearnya adalah y = 2/3x + 2
Jawab: y = 2/3x + 2
Persamaan seperti Contoh 1 pada halaman sebelumnya dinamakan persamaan sebuah garis.
Soal 1
Carilah persamaan-persamaan garis (1) sampai (4) pada gambar di sebelah kanan.
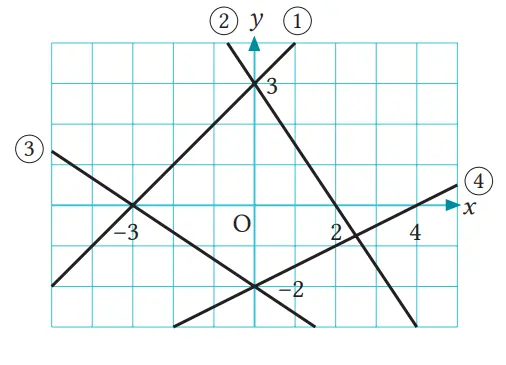
Jawaban:
① y = x + 3
② y = –3/2x + 3
③ y = –2/3x –2
④ y = 1/2x – 2
Marilah kita cari persamaan sebuah garis dengan koordinat salah satu titik dan kemiringannya diketahui.
Contoh 2
Carilah persamaan sebuah garis yang melalui titik (–3, 7) dan memiliki kemiringan –2.
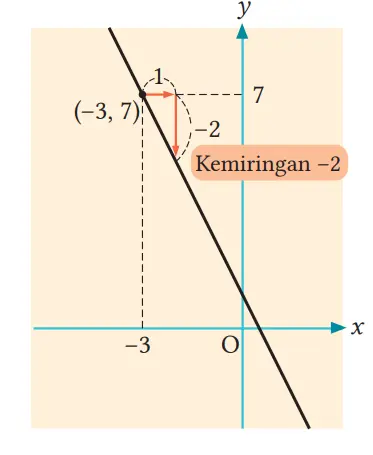
Penyelesaian
Misalkan persamaan garisnya y = ax + b. Karena a = –2
y = –2x + b 1
Kita ketahui garis melalui titik (–3, 7),substitusikan x = –3, y = 7 ke 1
7 = –2 × (–3) + b
Dengan menyelesaikan persamaan ini, kita peroleh b = 1.
Oleh karena itu, persamaan garisnya adalah y = –2x + 1.
Jawab: y = –2x + 1
Jika koordinat satu titik dan kemiringannya diketahui, maka dua titik dapat ditentukan kemudian suatu garis dapat ditentukan. Saat kemiringannya sudah mengetahuinhya, maka peserta didik dapat memahami bahwa garis tersebut dapat menentukannya setelah peserta didik menemukan intersep y.
Jika peserta didik berpikir secara kreatif, diharapkan peserta didik memperoleh bagian-bagian tersebut dengan metode berikut.
(1) Gambarlah garis dan tentukan bagian-bagiannya.
(2) Jika peserta didik mengulangi proses “1 unit ke kanan dan 2 unit ke bawah” dari titik (–3, 7) sebanyak tiga kali, peserta didik akan mendapatkan titik (0, 1).
(3) Jadi, jika bergerak dari titik (–3, 7) dengan “3 unit ke kanan dan 6 unit ke bawah”, akan diperoleh titik (0, 1).
Setelah mengetahui metode seperti itu, ajarkan cara menentukan intersep y dengan perhitungan. Kemudian, konfirmasikan bahwa perhitungan tersebut sesuai dengan nilai yang diperoleh dengan metode lain sehingga peserta didik dapat memahami validitas dan kegunaan perhitungan.
Soal 2
Carilah persamaan-persamaan dari garis-garis berikut.
(1) Garis yang melalui titik (2, 4) dan memiliki kemiringan 3.
Jawaban:
y = 3x – 2
(2) Garis yang melalui titik (–1, 2) dan kemiringan –2/3.
Jawaban:
y = –2/3x + 4/3
(3) Garis yang melalui titik (3, 5) dan sejajar garis y = x.
Jawaban:
y = x + 2
Mari kita cari persamaan sebuah garis bila koordinat dua titik diketahui.
Contoh 3
Carilah persamaan garis yang melalui titik (–4, 1) dan titik (2, 4).
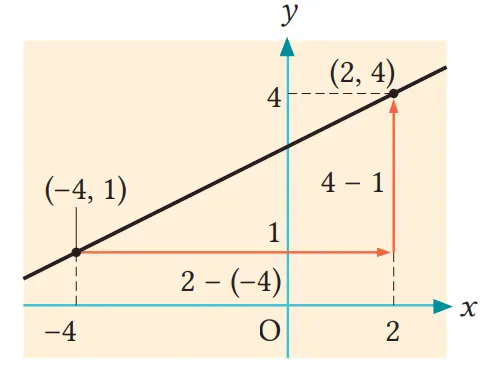
Penyelesaian
Misalkan persamaan garisnya y = ax + b. Karena garis melalui titik (–4, 1) dan titik (2, 4), maka tingkat perubahan adalah
a = (4 – 1)/(2 – (–4))
Jadi, y = 1/2x + b (1)
Substitusikan x = –4, y = 1 ke (1)
1 = 1/2× (–4) + b
Selesaikan terhadap b, maka kita peroleh b = 3.
Oleh karena itu, persamaan garisnya adalah
y = 1/2x + 3
Jawab: y = 1/2x + 3
Soal 3
Untuk Contoh 3, Toni berpikir seperti berikut.
Misalkan persamaannya y = ax + b.
Bila x = –4, y = 1, maka persamaan menjadi 1 = –4a + b. (1)
Bila x = 2, y = 4, maka persamaan menjadi 4 = 2a + b. (2)
Nilai-nilai a dan b dapat kita cari dengan menyelesaikan sistem persamaan (1) dan (2) .
Carilah persamaan garis dengan menggunakan cara Toni.
Jawaban:
Jika ① dan ② dapat terselesaikan sebagai sistem persamaan, maka kita peroleh
a = 1/2, b = 3
Jadi, persamaan garis yang dicari adalah y = 1/2x + 3.
Soal 4
Carilah persamaan-persamaan garis yang melalui pasangan titik-titik berikut.
(1) (2, 3), (4, 7)
(2) (–3, 11), (4, –10)
Jawaban:
(1) y = 2x – 1
(2) y = –3x + 2
Soal 5
Carilah persamaan dari garis di samping kanan.
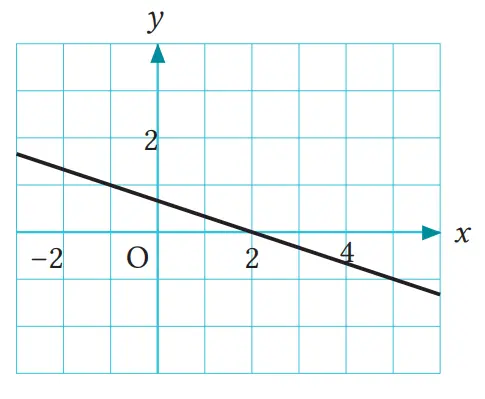
Jawaban:
Misalkan persamaan garis yang dicari adalah
y = ax + b.
Saat x = –1 maka y = 1, sehingga
1 = –a + b ①
Saat x = 2 maka y = 0, sehingga
0 = 2a + b ②
Jika ① dan ② dapat terselesaikan sebagai sistem persamaan, maka kita peroleh
a = –1/3, b = 2/3
Jadi, persamaan garis yang dicari adalah
y = –1/3x + 2/3.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
