ohgreat.id-Jawaban Ayo Mencoba halaman 78  Segitiga Istimewa Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 78. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 2 Teorema Pythagoras. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Segitiga Istimewa

Ayo Bereksplorasi

Pada bangunan minimalis seperti gambar di bawah, biasanya menggunakan kerangka segitiga yang memiliki ukuran sisi miring sama, baik dari sisi miring kanan dan kiri.

Gambar 2.7 Rumah Segitiga Minimalis

Berdasarkan gambar di atas diketahui bahwa bingkai yang menyangga kaca pada sisi depan atap berbentuk segitiga istimewa. Jika kita perhatikan dengan baik, segitiga istimewa pada bingkai kaca di atas berbentuk segitiga siku-siku sama kaki. Menggunakan aturan Teorema Pythagoras kalian akan dapat menentukan panjang dari ketiga sisi bingkai tersebut. Bagaimana kalian dapat menentukan ciri khusus dari segitiga siku-siku samakaki? Jika Anda hanya mengetahui satu sisi segitiga sama kaki, bagaimana cara menghitung panjang salah satu sisi segitiga siku-siku sama kaki?

Pembahasan

Segitiga siku-siku sama kaki adalah segitiga istimewa yang ukuran ketiga sudutnya adalah 45°-45°-90°. Semua segitiga siku-siku sama kaki adalah setengah persegi. Segitiga ABC di samping memiliki sisi siku-siku AB dan BC serta sisi miring AB. Diketahui bahwa sisi AB = BC = a maka panjang sisi miringnya adalah

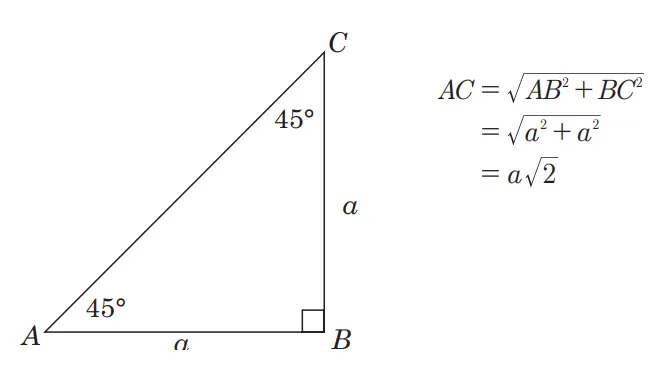
Berdasarkan perhitungan di atas diperoleh perbandingan sisi-sisinya adalah

AB:BC:AC = a:a:a√2

Sehingga, pada segitiga istimewa dengan sudut 45°, 90°, dan 45° memiliki panjang sisi miring √2 kali panjang dari sisi yang lain.

Ayo Mencoba

Sebagai pembuktian pada kegiatan sebelumnya, gunakan Teorema Pythagoras untuk menentukan panjang sisi hipotenusa setiap segitiga siku-siku sama kaki pada gambar di bawah. Kemudian sederhanakan setiap bentuk akar kuadratnya.

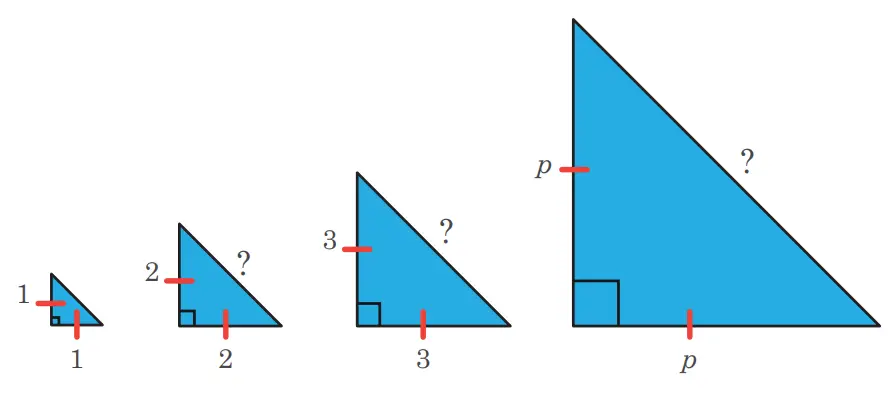
Salin dan lengkapi tabel berikut dengan melihat gambar sebelumnya.

Perhatikan panjang hipotenusa setiap kolom yang telah kalian lengkapi. Bagaimanakah pola yang terbentuk dari panjang sisi siku-siku dan panjang sisi miring pada segitiga siku-siku sama kaki di atas?

Jawaban:

Contoh 2.4

Diketahui suatu segitiga siku-siku sama kaki segitiga ABC dengan sudutC = 90°dan AB = 15 √2 cm . Hitunglah panjang AC.

Alternatif penyelesaian

Diketahui:

Berikut segitiganya

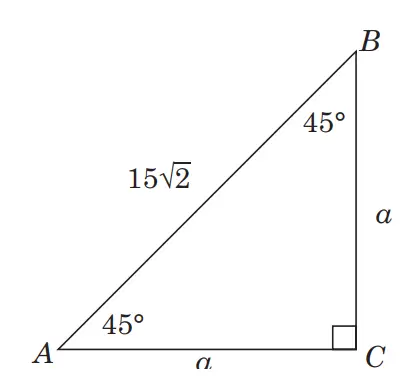
√1 : √2, Karena AC = CB maka

⇔AC : AB = 1 : √2
AC : 15√2 = 1 : √2
⇔AC x √2 = 1 x 15√2
AC = 15√2/√2
AC = 15 cm

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***