ohgreat.id-Jawaban Ayo Berpikir Kreatif halaman 79 Segitiga Istimewa Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 79. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 2 Teorema Pythagoras. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Segitiga Istimewa

Ayo Berpikir Kreatif

Perhatikan gambar dibawah ini.

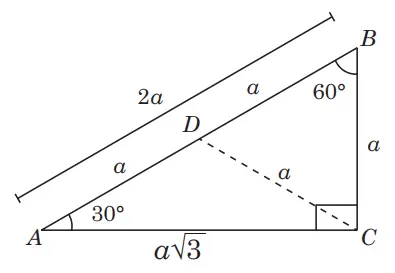
Segitiga ABC siku-siku di C dengan sisi miring AB dan sisi siku-sikunya AC dan BC, serta Sudut A = 30°, Sudut C = 90°, Sudut B = 60°

Kalian coba buktikan bahwa pada segitiga siku-siku yang sudut-sudutnya 30° dan 60°, perbandingan sisi terpendek dan sisi lainnya adalah 1 : 2 : √3

Contoh 2.5

Pada Segitiga ABC , sudut B = 60° dan sudut A = 30° . Panjang BC cm = 12 , hitunglah panjang:

a. AC

b. AB

Alternatif penyelesaian

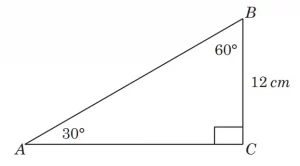
Menggunakan perbandingan pada segitiga istimewa yaitu panjang sisi miring adalah 2 kali sisi terpendek dan panjang sisi lainnya adalah √3 kali sisi terpendek.

a. AC/BC =√3/1 cm
AC/12 = √3/1
AC = 12√3 cm

b. AB/BC = 2/1 cm
AB/12 = 2/1
AB = 24 cm

Ayo Bekerja Sama

Gambar di bawah ini merupakan Theodorus yang pemberian nama berdasarkan nama pembuatnya yaitu Theodore dari Kirene. Theodore adalah orang yang memiliki pendapat yang sama dengan Pythagoras. Gambar Roda Theodorus dimulai dengan segitiga siku-siku dengan panjang kedua sisinya adalah 1 satuan panjang dan bergerak berlawanan arah jarum jam yang dapat ditunjukkan seperti gambar berikut.

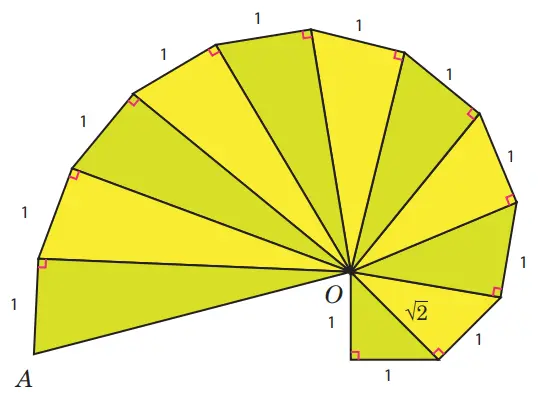
Gambar 2.8 Roda Theodorus

Coba kalian perhatikan gambar di atas, selanjutnya diskusikan dengan teman kalian dalam satu kelompok untuk membuktikan panjang hipotenusa setiap segitiga yang terbentuk, sehingga kalian akan menemukan panjang AO pada segitiga siku-siku terakhir dari Roda Theodorus di atas.

Jawaban:

Berikut alternatif penyelesaian yang dapat terbentuk.

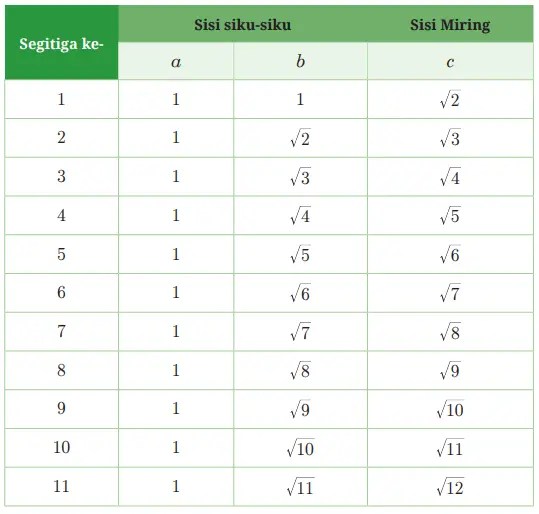
Dengan demikian, memperoleh panjang AO adalah √12

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***