ohgreat.id-Jawaban Ayo Bereksplorasi halaman 84 Penerapan Teorema Pythagoras Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 2. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 2 Teorema Pythagoras. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Penerapan Teorema Pythagoras
Ayo Bereksplorasi
Permainan Bentengan atau Rerebonan merupakan permainan yang dimainkan oleh dua kelompok penawan dan tertawan. Masing-masing kelompok terdiri atas empat hingga delapan orang. Lalu, memiliki satu tempat sebagai markas. Markas atau ‘benteng’ bisa berupa sebuah tiang, pohon, atau pilar.
Gambar 2.9 Anak-anak sedang bermain Bentengan atau Rerebonan
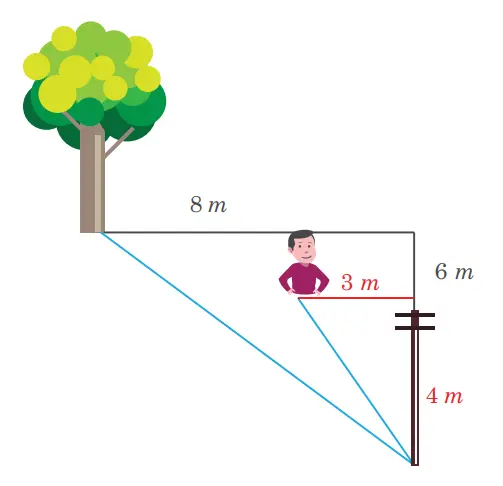
Apakah kalian pernah bermain bentengan? Jika Kalian berada 4 meter sebelah utara dan 3 meter sebelah timur dari benteng kalian. Benteng lawan kalian berada di 6 meter sebelah utara dan 8 meter sebelah timur dari benteng kalian. Bagaimanakah menentukan jarak kalian dengan benteng lawan kalian? Masalah ini bisa kalian selesaikan dengan menggunakan Teorema Pythagoras. Namun sebelumnya kalian pelajari terlebih dahulu kegiatan ini.
Gambar Tiang dan pohon
Titik awal yang kita gunakan untuk perhitungan adalah titik tumpu tiang pada tanah. Sehingga jarak antara titik awal dengan posisi kalian, serta jarak antara titik awal ke pohon sebagai daerah lawan yaitu titik tumpu pohon pada tanah dapat kita hitung, bisa dengan memanfaatkan tripel pythagoras.
Jarak antara dua titik
Perhatikan Gambar di atas. Setiap ruas garis yang tidak sejajar dengan sumbu-x maupun sumbu-y adalah hipotenusa dari segitiga siku-siku dari dua sisi yang sejajar dengan sumbu-x dan sumbu-y. Sehingga kalian bisa menentukan jarak dua titik pada bidang Cartesius dengan menggunakan Teorema Pythagoras.
Gambar Ilustrasi ruas garis yang membentuk Segitiga Siku-siku
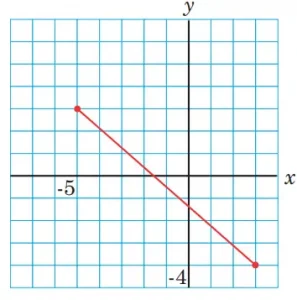
Untuk mengukur panjang ruas garis yang menghubungkan dua titik pada bidang koordinat, kita dapat menggambar titik-titik tersebut. Setelah itu, kita menentukan panjang setiap ruas garis. Namun, bagaimana jika titik-titik yang diketahui tidak memungkinkan untuk diplotkan pada bidang Cartesius? Misalkan, diminta untuk menentukan jarak antara titik A(−5, 3) dan B(3, −4). Bagaimana kita dengan mudah menentukan jarak dua titik pada bidang Cartesius?
Untuk menyelesaikan masalah di atas, lakukan kegiatan di bawah terlebih dahulu bagaimana menentukan jarak titik antara dua titik.
1. Gambar kedua titik A dan B pada bidang Cartesius. Tarik garis sehingga menghubungkan kedua titik. Gambar yang kalian buat akan tampak sama seperti pada gambar di halaman berikut.
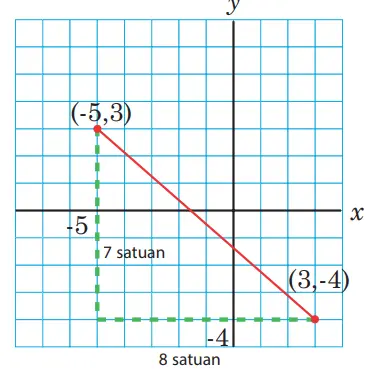
2. Pada gambar di poin (1) Apabila ditarik garis dari titik (-5, 3) dan (3, -4) yang sejajar dengan sumbu-x dan sumbu-y, maka kita bisa melihat suatu segitiga siku-siku dengan panjang sisi tegaknya adalah 7 satuan dan 8 satuan. Sehingga, kita bisa menggunakan teorema Pythagoras untuk menentukan jarak kedua titik tersebut.
Berdasarkan gambar di atas, dan menerapkan teorema Pythagoras jarak kedua titik sebagai sisi miring, berlaku
Sisi Miring = √(8² + 7²)
= √(64 + 49)
= √113
Sehingga, jarak kedua titik tersebut sebagai sisi miring adalah V113 satuan.
Contoh 2.6
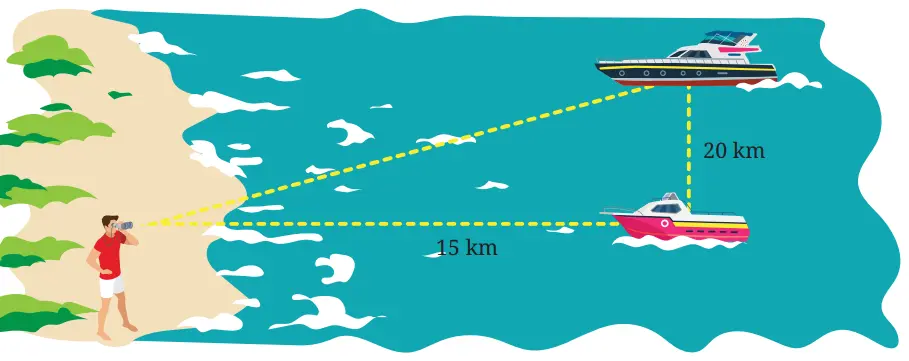
Aldo adalah seorang penjaga pantai yang selalu mengawasi kondisi pantai dan juga perahu-perahu yang akan bersandar di sekitaran pantai.
Suatu hari Aldo melihat dua perahu, yaitu perahu wisata dan perahu nelayan, seperti yang ditunjukkan pada gambar. Jika kecepatan rata-rata kedua perahu untuk mendekati pantai adalah 30 km/jam, tentukan selisih waktu yang ditempuh kedua perahu tersebut untuk mendekati pantai.
Alternatif penyelesaian
Berdasarkan gambar diketahui bahwa jarak Aldo dan perahu nelayan adalah 15 km, kemudian jarak kedua perahu adalah 20 km. Pada gambar juga diketahui bahwa jarak antara Aldo, perahu wisata dan perahu nelayan membentuk suatu segitiga siku-siku. Sehingga berlaku aturan dalam Teorema Pythagoras.
Menemukan jarak Aldo dengan perahu wisata.
Jarak Raja dengan Perahu Wisata =√(15² + 20²)
= √(225 + 400)
= √625 = 25
Dengan kecepatan 30 km/jam, maka waktu yang dibutuhkan untuk menempuh perjalanan perahu wisata menuju tempat Aldo adalah perjalanan perahu wisata = 25/30 = 0.82 jam.
0,83 jam itu setara dengan 50 menit.
Perjalanan perahu nelayan menuju tempat Aldo adalah perjalanan perahu nelayan = 15/30 = 0,5 jam
0,5 jam itu setara dengan 30 menit.
Dengan demikian, selisih antara perjalanan perahu wisata dan perahu nelayan menuju tempat Aldo adalah 50 ─ 30 = 20 menit.
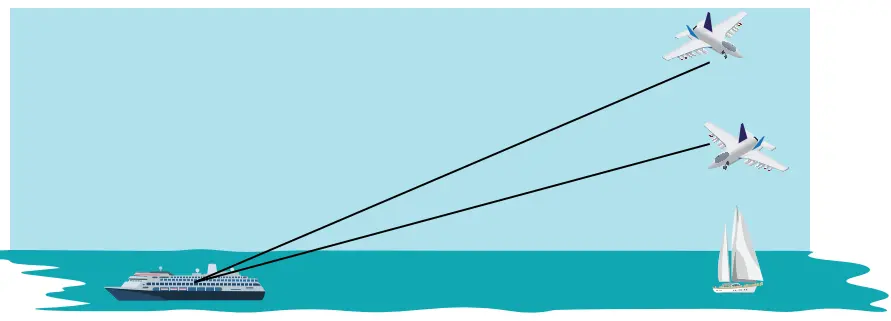
Contoh 2.7
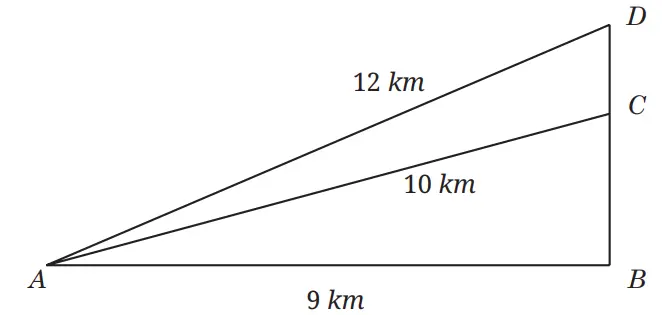
Dua pesawat sedang terbang melintasi kapal induk. Suatu radar yang berlokasi sejauh 9 km dari kapal induk mendeteksi bahwa posisi kedua pesawat tempur tersebut berjarak 10 km dan 12 km dari radar. Tentukan jarak kedua pesawat diukur berdasarkan ketinggiannya.
Alternatif penyelesaian
Perhatikan bahwa masalah di atas bisa digambarkan seperti berikut.
Berdasarkan gambar di atas, jarak kedua pesawat yang dimaksud adalah panjang CD.
Untuk menentukan panjang CD, terlebih dahulu kita akan menentukan panjang BC dan BD.
Berdasarkan Teorema Pythagoras,
BC² = AC² – AB²
= 10² -9²
= 100 – 81 = 19
BC =√19 = 4,35
BD² = AD² – AB²
= 12² – 9²
= 144 – 81 = 63
BD = √63 = 7,93
Maka DC = BD – BC = 7,93 – 4,35 = 3,58
Sehingga jarak kedua pesawat tersebut adalah 3,58 km .
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***