ohgreat.id-Dalil Pythagoras halaman 55 Menemukan Konsep Pythagoras Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 55. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 2 Teorema Pythagoras. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Daftar Isi
Menemukan Konsep Pythagoras
Dalil Pythagoras
Pada suatu segitiga siku-siku, luas persegi pada sisi miringnya sama dengan jumlah luas persegi lain pada kedua sisi siku-sikunya, hal ini juga berarti jumlah dari kuadrat kedua sisi siku-siku segitiga pada segitiga siku-siku sama dengan kuadrat panjang sisi miringnya (hipotenusa).
Teorema Pythagoras
Pada segitiga ABC siku-siku dengan siku-siku di B, berlaku:
c² = a² + b²
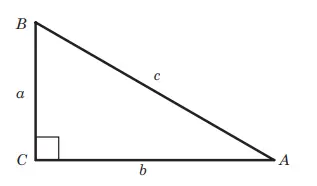
Secara matematis, seperti apakah Teorema Pythagoras? Berikut adalah salah satu pembuktian untuk memeriksa kebenaran Teorema Pythagoras.
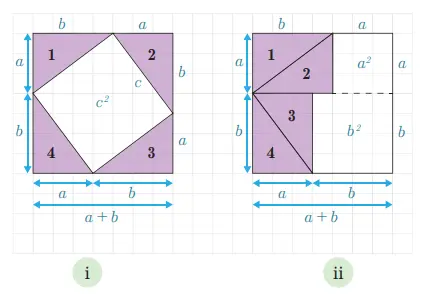
Gambar 2.4 Pembuktian Teorema Pythagoras
Berdasarkan Gambar 2.4. Kita dapat menemukan bentuk persamaan seperti berikut.
Pada Gambar 2.4 (i) dapat kita peroleh bahwa (a + b)² = 4 x ½ab + c² = 2ab + c²
Selanjutnya, perhatikan pada Gambar 2.4 (ii) dapat kita peroleh bahwa
(a + b)² = a² + 2ab + b²
Sehingga, berdasarkan Gambar 2.4(i) dan 2.4(ii) diperoleh
(a + b)² = (a + b)²
⇔2ab + c² = a² + 2ab + b²
c² + 2ab = a² + b² + 2ab
⇔c² + 2ab – 2ab = a² + b² + 2ab – 2ab
c² = a² + b²
Dengan demikian, luas persegi pada sisi hipotenusa adalah c², dan jumlah luas persegi pada kedua sisi tegaknya adalah a² + b²
Contoh 2.2
1. Tentukan panjang hipotenusa segitiga di bawah.
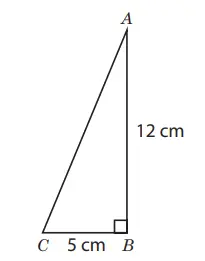
Alternatif penyelesaian
Diketahui:
AB = = 12 5 cm BC cm
Ditanya:
Hipotenusa atau panjang AC.
Jawab:
c² = a² + b²
AC² = AB² + BC²
= 12² + 5²
= 144 + 25
AC² = 169
AC = V169 = 13
Jadi, panjang hipotenusa = = AC 13 cm .
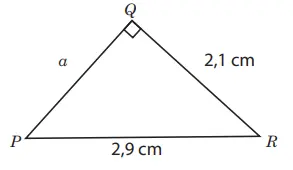
2. Tentukan panjang a pada segitiga berikut.
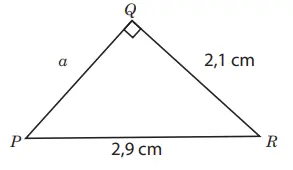
Alternatif penyelesaian
Diketahui:
misal
PR = = 29 21 , , cm QR , cm
Ditanya:
panjang a = PQ.
Jawab:
c² = a² + b²
PR² = PQ² + QR²
2,9² = PQ² + 2,1²
PQ² = 2,9² + 2,1²
PQ² = 8,41² + 4,41 = 4
PQ = √4 = 2
Jadi, panjang a = PQ = 2 cm
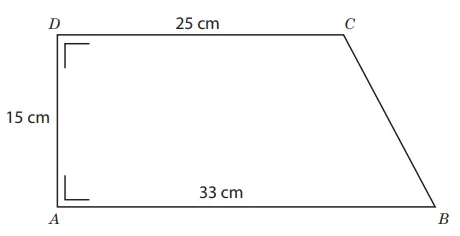
3. Perhatikan gambar trapesium berikut.
Alternatif penyelesaian
Diketahui:
AD = 15, CD = 25 cm, AB = 33cm
Ditanya:
Panjang BC adalah …
Jawab:
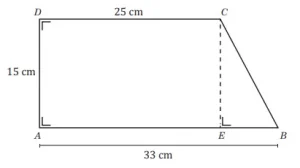
Untuk menyelesaikan masalah di atas, terlebih dahulu kita buat garis dari C dan tegak lurus dengan garis AB.
Misalkan titik potong dengan garis AB adalah E, maka terbentuk segitiga siku-siku BEC. Sehingga berlaku Teorema Pythagoras.
BC² = CE² + BE²
Panjang BE
BE = AB DC
BE = 33 – 25 = 8
Jadi, panjang BE cm = 8 .
Panjang CE = = AD 15 cm
Perhatikan segitiga BEC siku-siku di E
⇔BC² = CE² + BE²
BC² = 15² + 8²
⇔BC² = 225 + 64 = 289
BC = V289 = 17
Jadi, panjang BC adalah 17 cm.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
