ohgreat.id-Ciri-Ciri Fungsi halaman 163 Memahami Fungsi Matematika Jilid 2 SMP/MTs Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP/Mts Kelas 8 halaman 163. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika Jilid 2 SMP Kelas 8 Kurikulum Merdeka Bab 4 Relasi dan Fungsi. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Relasi dan Fungsi

Memahami Fungsi

Ciri-Ciri Fungsi

Ayo Mencoba

Perhatikan panduan pembuatan kata sandi berikut:

Kemudian, perhatikan juga daftar nama hewan berikut ini.

1. Komodo

2. Harimau

3. jalak

4. CENDRAWASIH

5. GAJAH

Nama-nama hewan yang disebutkan di atas adalah beberapa nama hewan langka yang harus dilindungi. Dengan menggunakan panduan yang diuraikan di atas, kalian dapat mengubah nama hewan menjadi kata sandi. Untuk menghindari sekedar membayangkan, pertimbangkan untuk melengkapi Tabel 4.2 (mungkin dalam spreadsheet yang berbeda) dengan memperhatikan kata sandi yang dibuat.

Tabel 4.2 Aturan Kata Sandi

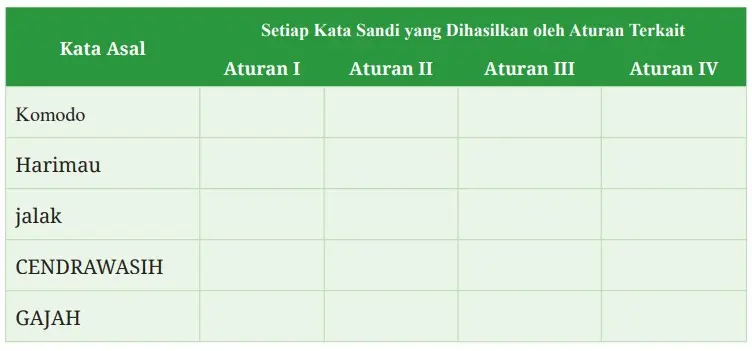
Periksa untuk melihat apakah kata sandi untuk setiap nama hewan memiliki sifat tunggal. Apakah setiap nama dikodekan menggunakan satu sandi saja?

Beberapa kemungkinan kata sandi dapat ditemukan pada tabel di bawah ini jika kalian bekerja cukup keras. Lengkapi isi tabel di bawah ini.

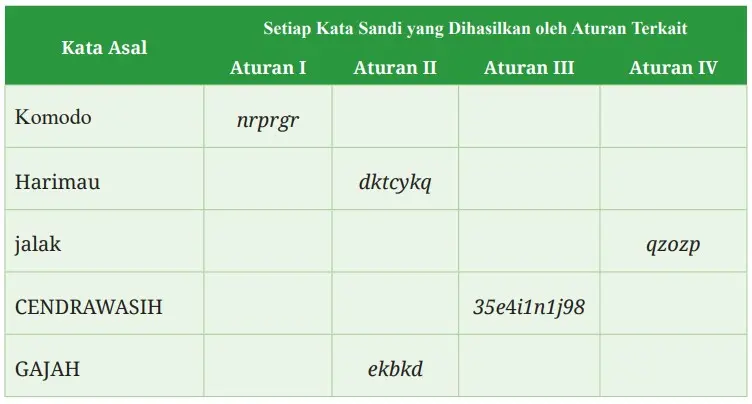
Kalian berhak mengajukan beberapa pertanyaan tertentu sebagai pemikir kritis dan kreatif. Berikut ini sebagai contoh:

1. Aturan manakah yang paling aman digunakan mulai dari aturan I hingga aturan IV? Mengapa demikian?

2. Kata “GAJAH” disandikan sebagai “ekbkd” menurut aturan II. Apa keuntungan dan kerugian dari aturan pengkodean ini?

3. Cari sedikitnya tiga pertanyaan lain yang sesuai dengan aturan penggunaan sandi seperti permasalahan di atas.

Pengertian:

Fungsi adalah relasi khusus yang menghubungkan setiap anggota daerah asal dengan tepat satu anggota daerah kawan.

Ayo Berpikir Kritis

Tasya mengatakan bahwa setiap relasi pasti bisa disebut sebagai fungsi, akan tetapi setiap fungsi belum tentu disebut sebagai relasi. Sedangkan Rosi justru mengatakan bahwa setiap relasi belum tentu bisa disebut sebagai fungsi, akan tetapi setiap fungsi pasti bisa disebut sebagai relasi. Mereka berdua sepakat bahwa pendapatnya adalah benar. Setujukah kalian dengan salah satu pendapat dari meraka? Jelaskan.

Berikut Alternatif Jawaban “Ayo Berpikir Kritis” yang Bernilai Benar. Setiap relasi belum tentu merupakan fungsi, akan tetapi setiap fungsi pasti merupakan relasi.

Untuk bentuk model kegiatan kreatif ini, diserahkan sepernuhnya kreatiitas teman Guru.

Kemudian, Ajak siswa untuk memahami Contoh 4.5 dan 4.6 serta alternatif penyelesaiannya

Contoh 4.5

Misalkan diketahui himpunan P = {3, 4, 5, 6, 7} dan himpunan Q = {4, 5, 7, 9}. “satu lebihnya dari” adalah relasi yang ditentukan. Apakah hubungan antara P dan Q merupakan fungsi?

Alternatif penyelesaian

Lakukan langkah-langkah berikut untuk menentukan apakah hubungan dari himpunan P ke himpunan Q merupakan fungsi atau bukan.

Hubungan antara himpunan P dan Q diketahui adalah satu lebihnya dari.

Jadi, kumpulan pasangan berurutan dapat digunakan untuk menggambarkan hubungan ini, yaitu {(5,4), (6,5)}.

Periksa anggota himpunan P yang tidak terhubung ke himpunan Q.

Angka-angka 3, 4, dan 7 adalah anggota himpunan P yang tidak memiliki pasangan di himpunan Q.

Kasus seperti ini karena tidak ada bilangan x dalam himpunan Q yaitu “3 adalah satu lebihnya dari x dalam himpunan Q”, “4 adalah satu lebihnya dari x dalam himpunan Q”, atau “7 adalah satu lebihnya dari x dalam himpunan Q”.

Karena ada anggota himpunan P tidak memiliki pasangan di himpunan Q, maka relasi ini bukan merupakan fungsi dari himpunan P ke himpunan Q.

Contoh 4.6

Misalkan ketahui himpunan R = {3, 6, 9, 12} dan himpunan S = {1, 2, 3, 4, 5, 6}. “Anggota R adalah tiga kali anggota S” merupakan relasi yang telah ditentukan. Apakah relasi himpunan R dan S merupakan fungsi?

Alternatif penyelesaian

Lakukan langkah-langkah berikut untuk menentukan apakah relasi dari himpunan R ke himpunan S merupakan fungsi atau bukan fungsi.

Ketahui bahwa relasi dari himpunan R ke himpunan S diketahui merupakan anggota himpunan R tiga kali anggota himpunan S.

Kemudian dapat kalian nyatakan dalam bentuk pasangan berurutan seperti berikut ini: {(3, 1); (6, 2); (9, 3); (12, 4)}.

Coba kalian perhatikan, berbeda dengan contoh soal sebelumnya bahwa setiap anggota R mempunyai pasangan ke S, meskipun anggota di S beberapa tidak memiliki pasangan, yakni: Beberapa anggota S yang tidak berpasangan adalah 6 dan 7

Oleh karena itu, relasi ini merupakan fungsi dari himpunan R ke himpunan S, karena setiap anggota himpunan R memiliki pasangan di himpunan S.

Ayo Bereksplorasi

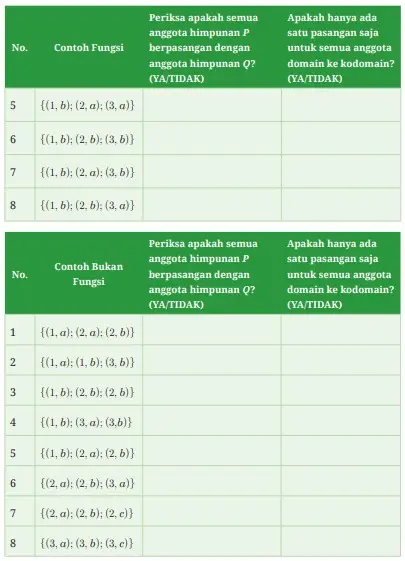
Perhatikan dengan cermat pada Tabel 4.3, pahami dan temukan alasan terkait karakteristik contoh fungsi dan bukan fungsi. Komunikasi hasil temuan kalian dengan penjelasan yang lugas dan menarik. Apabila kita ketahui relasi dari himpunan P ke Q adalah P = {1, 2, 3} dan Q = {a, b}, maka Tabel 4.3 berikut contoh fungsi dan bukan fungsi yang dapat kalian buat.

Tabel 4.3 Contoh Fungsi dan Bukan Fungsi

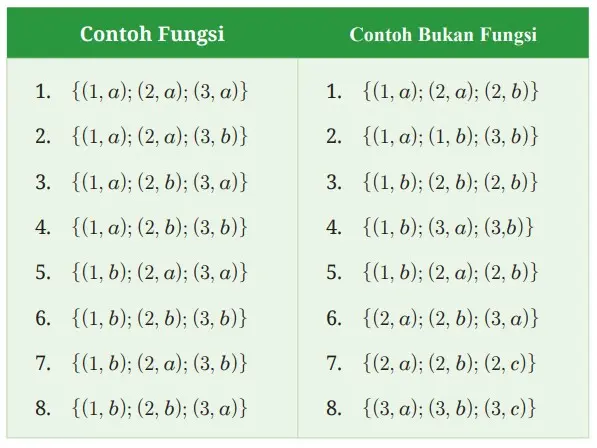
Coba pusatkan perhatikan kalian pada dua pertanyaan di bawah ini.

1. Apakah setiap anggota himpunan P terhubung dengan anggota himpunan Q?

2. Berapa banyak anggota himpunan Q yang terhubung pada satu anggota himpunan P?

Selanjutnya, lengkapilah isi Tabel 4.6 berikut ini.

Tabel 4.4 Statement Fungsi dan Bukan Fungsi

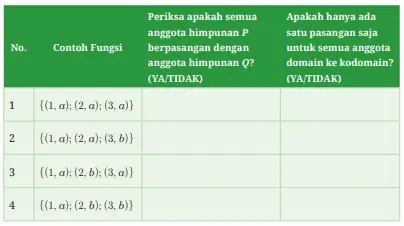
Kemudian, pada pada lembar kerja kalian, catat kesimpulan kalian berdasarkan kegiatan di atas.

Alternatif Penyelesaian

1. Benarkah setiap anggota himpunan P selalu dipasangkan dengan anggota himpunan Q?

Jawabannya adalah iya, untuk daftar contoh fungsi Tidak, untuk contoh bukan fungsi

2. Ada berapa banyak anggota himpunan Q yang dihubungkan dengan satu anggota himpunan A?

Jawaban untuk bagian daftar contoh fungsi adalah ada sebanyak 2

Jawaban untuk bagian daftar contoh bukan fungsi adalah ada sebanyak 2

Berdasarkan aturan pemasangan dari himpunan P = {1, 2, 3} ke himpunan Q = {a, b}; tabel berikut sebagai alternatif jawabannya.

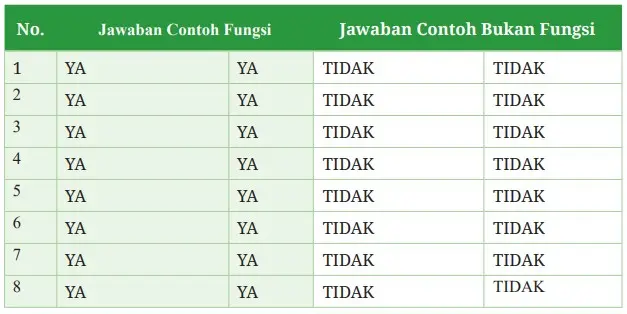
Dengan demikian, fungsi pada dasarnya adalah aturan yang menetapkan setiap anggota daerah ke tepat satu anggota daerah kawan.

Ayo Berpikir Kreatif

Buatlah hipotesis atau dugaan tentang sifat-sifat suatu fungsi dan tuliskan di atas kertas kalian.

Kemudian, coba diskusikanlah dengan rekan-rekan kelompok kalian tentang suatu fungsi yang dapat kalian buat dengan menggabungkan dari kedua himpunan di bawah ini.

a. K = {1, 2, 3, 4} ke L = {p, q}

b. M = {p, q} ke N = {1, 2, 3, 4}

Berdasarkan kegiatan tersebut, coba kalian simpulkan.

Selanjutnya, cobalah kalian terapkan hasil kesimpulan tersebut dalam memeriksa apakah kesimpulan yang kalian dapatkan adalah benar atau tidak?

Berikut Alternatif Jawaban.

Langkah-langkah Kegiatan Berpikir Kreatif ini Kita serahkan sepenuhnya kepada teman Guru untuk menyusunnya sendiri, sebagai latihan. Kemudian perkirakan sendiri juga kesimpulan yang kalian dapat.

Atau jika tidak memungkinkan, jadikanlah sebagai tugas individu untuk kalian jadikan sebagai nilai tambahan untuk Ulangan Harian.

Ayo Berkomunikasi

Menentukan Banyak Fungsi yang Mungkin

Ketahui A = {a}; B = {5, 7} dan C = {x, y, z}

Sajikan dengan cara diagram panah terhadap fungsi berikut ini:

1. fungsi A ke B

2. fungsi A ke C

3. fungsi B ke C

4. fungsi C ke A

5. fungsi C ke B

Kemudian, lengkapi Tabel 4.5 berikut berdasarkan hasil kerja kalian dapatkan.

Tabel 4.5 Banyak Fungsi yang Mungkin

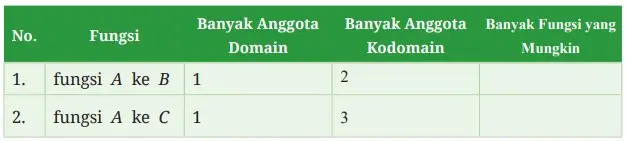
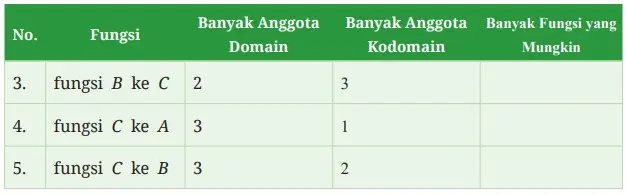
Apa kesimpulan yang kalian dapatkan berdasarkan hasil pada tabel tersebut di atas? Jelaskan.

Berikut Alternatif Kegiatan.

Coba kalian perhatikan alternatif penyelesaiannya yang kelompok kalian kerjakan. Jika ada temanmu yang kurang mengerti, karena jawaban kurang lengkap. Coba apa yang perlu kalian tambahkan dalam dalam penyelesaian tersebut agar lebih lengkap dan jelas sehingga temanmu lebih mengerti.

Dalam kegiatan ini siswa diminta untuk memahami permasalahan yang berkaitan dengan banyak suatu fungsi. Berilah kesempatan siswa untuk memahami terlebih dahulu, dan berilah kesempatan kepada siswa yang sudah memahami untuk mempresentasikan atau menjelaskan kepada siswa lainnya.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***