ohgreat.id-Jawaban Bagaimana Cara Menentukan Peluang halaman 176 Peluang Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 176. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 6 Peluang. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Peluang

Bagaimana Cara Menentukan Peluang

Q. Ketika sebuah dadu dilempar, manakah yang kemungkinan lebih sering muncul, mata dadu 1 atau mata dadu 3?

Jawaban:

Menganggap Peluang keluarnya mata dadu  sama untuk kedua mata dadu.

Jika sebuah dadu bersisi sama Kita lempar, maka kita dapat berharap bahwa kemungkinan munculnya tiap mata dadu adalah sama. Pada situasi ini, kita dapat menyatakan bahwa kemungkinan munculnya mata dadu 1 sampai dengan 6 adalah sama secara kemungkinan.

Ketika kita melempar sebuah dadu, banyaknya kejadian yang berbeda akan muncul adalah 6. Karena itu, peluang munculnya tiap mata dadu dari mata 1 sampai dengan 6 adalah 1/6
.
Peluang munculnya mata dadu 3 sebesar 0,17 dan hasil dari beberapa kali percobaan di halaman 174, nilainya hampir sama dengan 1/6.

Contoh 1

Ketika sebuah kartu kita ambil dari 52 kartu remi, kita dapat menyatakan bahwa kemungkinan terambilnya sebuah kartu adalah sama. Dalam hal ini, peluang terambilnya sebuah kartu adalah 1/52
.
Soal 1

Pilih salah satu yang memiliki kemungkinan sama terjadi dari situasi-situasi berikut.

(1) Melempar dadu bermata 1 sampai dengan 6 bila dadu yang dilempar adalah seperti pada gambar di kanan.

(2) Kejadian munculnya gambar atau angka ketika sebuah uang logam dilempar.

(3) Kejadian tutup botol telungkup atau telentang ketika sebuah tutup botol dilempar.

Jawaban:

(2) Kejadian munculnya gambar atau angka ketika sebuah uang logam dilempar.

Soal 2

Beri beberapa contoh kejadian di sekitar kita yang memiliki kemungkinan terjadinya adalah sama.

Jawaban:

(Contoh)

Lempar koin, lotre, roulette, bingo

Marilah kita cari peluang-peluang kejadian yang memiliki kemungkinan yang sama.

Bila sebuah dadu bersisi enam kita lempar, kita dapat menentukan peluang munculnya mata dadu genap seperti berikut. Dalam kasus ini, banyaknya kemungkinan kejadian adalah 6 buah.

Karena tiga kejadian berupa munculnya mata dadu genap seperti menunjukkan pada gambar di sebelah kanan, maka (peluang munculnya mata dadu genap) adalah 3/6 = 1/2

Bila kita memperhatikan semua kemungkinan kejadian dan tiap kejadian memiliki kemungkinan sama terjadi, maka peluang kejadian dapat kita tentukan seperti berikut.

Jika total seluruh kejadian adalah n, dan ada sebanyak a kejadian, maka peluang terjadinya kejadian tersebut adalah

p = a/n

Contoh 2

Tentukan peluang kejadian munculnya kartu hati yang diambil dari 52 kartu remi yang dikocok!

Cara

Kejadian pengambilan tiap kartu dari 52 kartu adalah sama. Tentukan peluang terambilnya kartu hati bila ada 13 kartu hati.

Penyelesaian

Kemungkinan terambilnya satu dari 52 kartu remi adalah sama. Dari 52 kartu, 13 di antaranya adalah kartu hati. Jadi, peluang terambilnya kartu hati adalah

13/52 = 1/4

Jawaban : 1/4

Soal 3

Carilah peluang kejadian berikut pada Contoh 2 (di halaman 177).

(1) Terambilnya sebuah kartu wajik.

Jawaban:

13/52 = 1/4

(2) Terambilnya sebuah kartu berangka 8.

Jawaban:

4/52 = 1/13

(3) Terambilnya kartu bergambar.

Jawaban:

12/52 = 3/13

(4) Terambilnya sebuah kartu hati atau satu kartu wajik.

Jawaban:

26/52 = 1/2

Soal 4

Pada sebuah kantong terdapat lima kelereng berukuran sama dengan nomor 1 sampai dengan 5. Ketika sebuah kelereng diambil dari kantong, tentukan peluang terambilnya kelereng bernomor genap, dan tentukan pula terambilnya kelereng bernomor ganjil.

Jawaban:

Peluang terambilnya kelereng bernomor genap 2/5

Peluang terambilnya kelereng bernomor ganjil 3/5

Mari kita pikirkan tentang rentang nilai peluang suatu kejadian.

Q. Seperti ditunjukkan pada gambar di sebelah kanan, pada kantong A – E terdapat masing-masing 4 kelereng. Bila 1 kelereng diambil dari setiap kantong, tentukan peluang terambilnya kelereng putih dari setiap kantong.

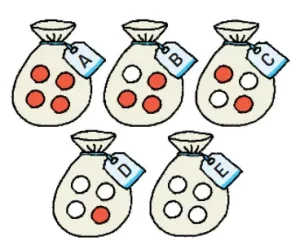
Jawaban:

A. 0/4 = 0

B. 1/2

C. 2/4 = 1/2

D. 3/4

E. 4/4 = 1

Pada , Untuk kantong A, apa pun kelereng yang diambil, tak akan pernah terambil kelereng putih, sehingga peluang terambil kelereng warna putih adalah 0/4 = 0. Untuk kantong E, apa pun kelereng yang kamu ambil, pasti akan terambil kelereng warna putih, sehingga peluang terambilnya kelereng putih adalah 4/4 = 1.

Untuk kantong-kantong lain, peluang terambilnya kelereng warna putih dapat dinyatakan dalam rentang nilai antara 0 dan 1, dinyatakan dengan angka antara 0 dan 1.

a. Jika kita misalkan peluang terjadinya kejadian adalah p, maka rentang nilai p adalah 0 ≤ p ≤ 1.

b. Jika p = 0, maka kejadian tidak akan mungkin terjadi.

c. Jika p = 1, maka kejadian akan pasti terjadi.

Soal 5

Berilah contoh-contoh kejadian yang memiliki peluang 0 atau 1.

Jawaban:

(Contoh)

Peluangnya 0…. peluang keluarnya mata dadu 7 ketika melempar undi dadu

Peluangnya 1… peluang keluarnya mata dadu lebih dari 1 ketika melempar undi dadu

Q. Ketika sebuah dadu bersisi enam dilemparkan, tentukanlah peluang kejadian berikut.

(1) Munculnya mata dadu 6

Jawaban:

1/6

(2) Tidak munculnya mata dadu 6

Jawaban:

5/6

Bila peluang suatu kejadian A muncul adalah p, maka peluang kejadian tidak munculnya A adalah 1 – p.

Soal 6

Dalam sebuah permainan, peluang menang adalah 3/20 . Tentukan peluang kekalahan dari permainan tersebut.

Jawaban:

1 – 3/20 = 17/20

Soal 7

Bila satu kartu diambil dari 50 kartu bernomor 1 sampai dengan 50, carilah peluang terambilnya kartu bernomor bilangan prima dan peluang terambilnya kartu bernomor bukan bilangan prima.

Jawaban:

Karena ada 15 bilangan prima dari 1 sampai dengan 50, yaitu 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, maka

a. Perbandingan kartu berangka bilangan prima adalah 15/50 = 3/10
.
b. Perbandingan kartu berangka bukan bilangan prima adalah 1 – 3/10 = 7/10.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***