ohgreat.id-Jawaban Soal Ringkasan halaman 164 Bab 5 Segitiga dan Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 164 Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Soal Ringkasan
Gagasan Utama
1. Isilah [ ] pada pertanyaan-pertanyaan berikut.
(1) Garis bagi dari [ ] pada segitiga sama kaki membagi alasnya menjadi dua bagian yang sama dan berpotongan tegak lurus dengan alas tersebut.
Jawaban:
Sudut puncak
(2) Pada dua segitiga siku-siku, jika panjang hipotenusa-hipotenusa yang bersesuaian dan [ ] adalah sama, atau panjang hipotenusa-hipotenusa bersesuaian dan [ ] adalah sama, maka kedua segitiga tersebut kongruen.
Jawaban:
Satu sudut lancip, sisi lainnya
(3) Kedua diagonal jajargenjang berpotongan di[ ] .
Jawaban:
Titik tengah kedua diagonal
(4) Persegi panjang didefinisikan sebagai [ ] .
Jawaban:
Segi empat dengan empat sudut yang sama
2. Pada segitiga sama kaki ABC, dengan sudut puncak ∠A = 36°, buatlah garis bagi ∠B dan misalkan D titik potong dengan sisi AC. Jawablah pertanyaan berikut.
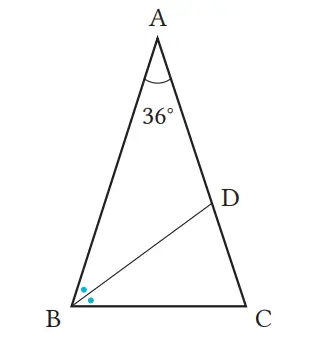
(1) Hitung ∠BDC.
Jawaban:
∠BDC = 72°
(2) Jenis segitiga apakah ∆BCD itu? Jelaskan!
Jawaban:
Segitiga sama kaki
⟨Alasan⟩ ΔABC adalah segitiga sama kaki dengan sudut puncak ∠A = 36°.
∠C = 72°. Juga, dari (1), ∠BDC = 72°.
Oleh karena itu, dalam ΔBCD, maka ∠C = ∠BDC.
Oleh karena itu, ΔBCD adalah segitiga sama kaki.
3. Dari titik-titik sudut A dan C pada jajargenjang ABCD, buatlah berturut-turut garis AE dan CF yang tegak lurus dengan diagonal BD. Jawablah pertanyaan berikut.
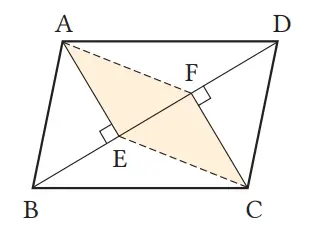
(1) Buktikan bahwa ∆ABE ≅ ∆CDF.
Jawaban:
Dari asumsi, ∠AEB = ∠CFD = 90° dalam ΔABE dan ΔCDF ①
Karena sudut dalam berseberangan dari garis sejajar adalah sama, dan AB // DC, maka ∠ABE = ∠CDF ②
Karena sisi berlawanan dari jajargenjang adalah sama, maka AB = CD ③
Dari (1), (2), dan (3), serta menurut kekongruenan segitiga siku-siku dengan sudut lancip sama, maka ΔABE ≅ ΔCDF.
(2) Dapat dibuktikan bahwa segi empat AECF adalah jajargenjang seperti berikut. Isilah [ ] , dan lengkapi pembuktiannya.
[ Bukti ]
∆ABE ≅ ∆CDF, sehingga AE = [ ] (1)
Berdasarkan yang diketahui, maka ∠AEF = ∠CFE [ ] adalah sama, sehingga AE // [ ](2)
Dari 1 dan 2 , dan karena [ ], maka segi empat AECF adalah jajargenjang.
Jawaban:
CF, sudut dalam berseberangan pasangan sisi sejajar dan sama.
4. Seperti ditunjukkan pada gambar di sebelah kanan, ambil titik C pada segmen AB dan buat segitiga sama sisi ACP dan CBQ dengan berturut-turut menggunakan AC dan BC. Jawablah pertanyaan berikut.
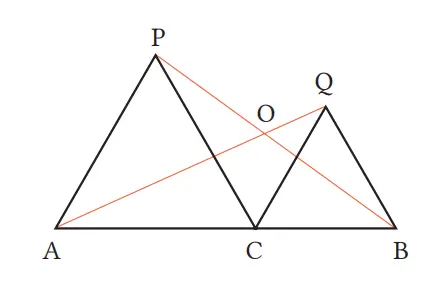
(1) Buktikan bahwa AQ = PB.
Jawaban:
Pada ΔACQ dan ΔPCB, dari asumsi,
AC = PC ①
CQ = CB ②
Karena satu sudut dalam dari segitiga sama sisi adalah 60°,
∠ACQ = ∠ACP + ∠PCQ = 60° + ∠PCQ
Dan ∠PCB = ∠PCQ + ∠QCB = ∠PCQ + 60°
Oleh karena itu, ∠ACQ = ∠PCB ③
Dari (1), (2), dan (3), serta menurut aturan kekongruenan sudut-sisi-sudut, maka ΔACQ ≅ ΔPCB
Karena sisi-sisi yang bersesuaian dari bangun-bangun yang kongruen adalah sama, maka AQ = PB.
(2) Jika O adalah titik potong AQ dan PB, carilah ∠AOP.
Jawaban:
60 °
Dari (1), maka ∠QAC = ∠BPC
∠PAO + ∠OPA = 120°
sehingga pada ΔAOP, ∠AOP = 180° – (∠PAO + ∠OPA) = 60°
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
