ohgreat.id-Jawaban Aktivitas Matematis halaman 159 Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 159. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Segi Empat

Aktivitas Matematis

Mari kita diskusikan syarat tambahan yang diperlukan agar jajargenjang menjadi persegi panjang, belah ketupat, dan persegi.

1. Jika kita tambah syarat a dan b berikut pada Jajargenjang ABCD, jenis segi empat apa yang akan terbentuk?

a. AB = BC

b. ∠A = 90°

Jawaban:

1) Ditambah ⓐ saja, belah ketupat

2) Ditambah ⓑ saja, persegi panjang

3) Ditambah ⓐ dan ⓑ sekaligus, persegi

2. Jika AB = BC pada Jajargenjang ABCD, maka Dewi menyatakan bahwa segi empat yang terbentuk adalah belah ketupat seperti berikut.

Cara Dewi

Sisi-sisi yang berhadapan pada jajargenjang sama panjang, sehingga AB = DC dan AD = BC. Jika saya tambahkan syarat AB = BC, maka sisi-sisi yang berdekatan akan sama panjang. Akibatnya, semua sisi sama panjang. Dengan demikian, ABCD adalah belah ketupat.

Jika ∠A = 90° pada Jajargenjang ABCD, maka jelaskan bahwa segi empat yang terbentuk adalah persegi panjang.

Jawaban:

(Contoh)

Dari teorema sifat jajargenjang, maka ∠A = ∠C, ∠B = ∠D.

Jika syarat ∠A = 90° ditambahkan, maka ∠A = ∠C = 90°.

Pada saat ini, karena jumlah sudut dalam dari segi empat adalah 360°, maka ∠B + ∠D + 180° dan ∠B = ∠D = 90°. Jadi, keempat sudutnya sama.

Oleh karena itu, ABCD menjadi persegi panjang.

3. Agar jajargenjang menjadi persegi panjang dan belah ketupat, syarat apa saja yang perlu ditambah? Bagaimana agar menjadi persegi, syarat apa lagi yang perlu ditambahkan? Pikirkan syaratnya dan jelaskan.

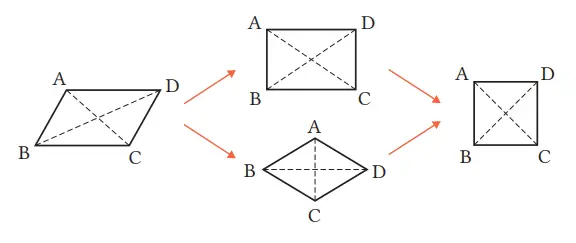
Jawaban:

(Contoh)

(1) Persegi panjang … AC = BD

⟨Alasan⟩

Ketika kondisi AC = BD tambahkan ke jajargenjang, itu menjadi ΔABC.

ΔDCB memiliki tiga set sisi yang sama-sama kongruen. Dari sini, dapat  kita katakan bahwa ∠ABC = ∠DCB. Jika sudut yang berdekatan dari jajargenjang sama, maka keempat sudutnya sama.

Oleh karena itu, ABCD berbentuk persegi panjang.

(2) Belah ketupat … AC ⊥ BD

⟨Alasan⟩

Misalkan O adalah perpotongan dari garis diagonal. Ketika kondisi AC ⊥ BD tambahkan ke jajargenjang, ΔABO dan ΔADO memiliki dua sisi dan sudut di antara keduanya sama dan kongruen. Dari sini dapat kita katakan bahwa AB = AD. Jika sisi-sisi yang berdekatan dari jajargenjang sama, maka keempat sisinya sama. Karena itu, ABCD adalah belah ketupat.

(3) Persegi … AC = BD, AC ⊥ BD

⟨Alasan⟩

Dengan cara serupa seperti ① dan ②, jika kondisi AC = BD dan AC ⊥ BD tambahkan ke jajargenjang, maka keempat sudut dan empat sisinya akan sama. Oleh karena itu, ABCD adalah persegi.

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***