ohgreat.id-Jawaban Sifat Jajargenjang halaman 149 Segi Empat Matematika SMP Kelas 8 Kurikulum Merdeka Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 49. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Segi Empat
Sifat Jajargenjang
Q. Putar jajargenjang ABCD terhadap titik O sebagai pusat perputaran. Mari periksa berikut ini dengan memotong dan mencocokkan gambar di akhir buku 4 dengan gambar di sebelah kanan.
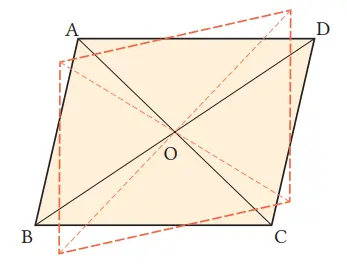
(1) Segitiga mula-mula mana yang tepat sama dengan ∆ABD?
Jawaban:
ΔCDB
(2) Pasangan segitiga mana yang tepat sama selain ∆ABD?
Jawaban:
ΔABC dan ΔCDA
ΔABO dan ΔCDO
ΔAOD dan ΔCOB
Pada segi empat, dua sisi yang berlawanan disebut sisi-sisi berhadapan, dan dua sudut yang berlawanan satu sama lain dinamakan sudut-sudut berhadapan.Jajargenjang didefinisikan sebagai berikut.
Segi empat yang memiliki dua pasang sisi berhadapan yang sejajar dinamakan jajargenjang.
Soal 1
Dari Q, pada segi empat, sifat-sifat apakah bila dilihat dari sisi, sudut, dan diagonal yang dapat kita cari?
Jawaban:
a. Kedua pasang sisi berhadapan adalah sama panjang.
b. Kedua pasang diagonalnya sama panjang.
c. Kedua diagonal berpotongan di titik tengah diagonal.
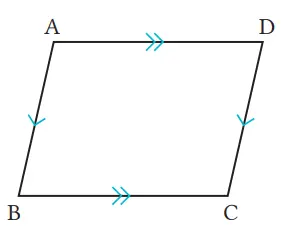
Kita dapat menyatakan pernyataan “dalam jajargenjang, dua pasang sisi berhadapan panjangnya sama” seperti berikut, menggunakan gambar di sebelah kanan. Pada segi empat ABCD.
(Diketahui) AB // DC, AD // BC
(Kesimpulan) AB = DC, AD = BC
Soal 2
Pada jajargenjang ABCD di atas, untuk membuktikan bahwa AB = DC dan AD = BC, pasangan segitiga yang mana yang perlu dibuktikan kongruen? Cobalah pikirkan garis-garis mana yang perlu ditarik untuk membentuk segitiga.
Jawaban:
ΔABD dan ΔCDB
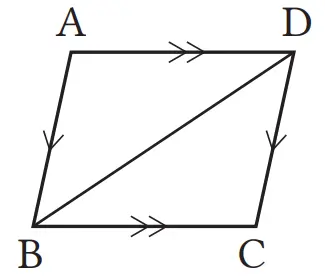
atau ΔABC dan ΔCDA
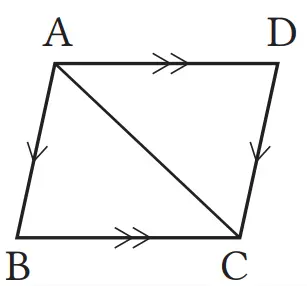
Contoh 1
Pada jajargenjang ABCD, buktikan bahwa AB = DC dan AD = BC.
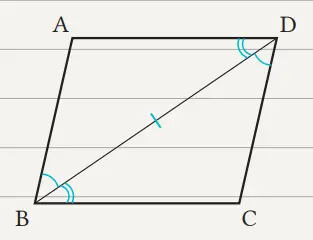
Buat diagonal BD. Pada ∆ABD dan ∆CDB, sudut-sudut dalam berseberangan dari garis-garis sejajar besarnya sama.
Karena AB // DC, maka ∠ABD = ∠CDB ①
Karena AD // BC, maka ∠ADB = ∠CBD ②
Dan BD adalah sisi persekutuan ③
Dari ①, ②, dan ③, menurut aturan kekongruenan
Sudut-Sisi-Sudut, maka ∆ABD ≅ ∆CDB
Dengan demikian AB = DC, AD = BC.
Dari ∆AOP ≅ ∆BOP yang ditunjukkan pada pembuktian di Contoh 1 , kita dapat simpulkan bahwa ∠A =∠C.
Soal 3
Pada jajargenjang ABCD di Contoh 1, buktikan bahwa ∠ABC = ∠CDA.
Jawaban:
Dari bukti Contoh 1, ΔABD ≅ ΔCDB
Dari ini, ∠ABD = ∠CDB ①
∠ADB = ∠CBD ②
Dari ①, ②
∠ABD + ∠CBD = ∠CDB + ∠ADB
Oleh karena itu, ∠ABC = ∠CDA
(Bukti terpisah)
Gambarlah AC diagonal.
Di ΔABC dan ΔCDA
Karena sudut dalam berseberangan dan
AB // DC, maka ∠BAC = ∠DCA ①
Dari AD // BC, ∠ACB = ∠CAD ②
Juga, AC sisi persekutuan ③
Dari ①, ②, ③, dan menurut aturan kekongruenan
sudut-sisi-sudut, maka ΔABC ≅ ΔCDA
Oleh karena itu, ∠ABC = ∠CDA.
Soal 4
Pada jajargenjang ABCD, jika kita misalkan O adalah titik potong kedua diagonalnya, maka buktikan bahwa AO = CO dan BO = DO.
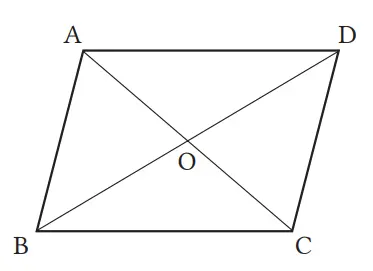
Jawaban:
Karena sudut dalam berseberangan di ΔABO dan ΔCDO untuk garis sejajar AB//DC, dan dari AB // DC, maka
∠BAO = ∠DCO ①
∠ABO = ∠CDO ②
Karena sisi berlawanan dari jajargenjang, maka
AB = CD ③
Dari (1), (2), dan (3), dan menurut aturan kekongruenan sudut-sisi-sudut, maka
ΔABO ≅ ΔCDO
Oleh karena itu, AO = CO, BO = DO
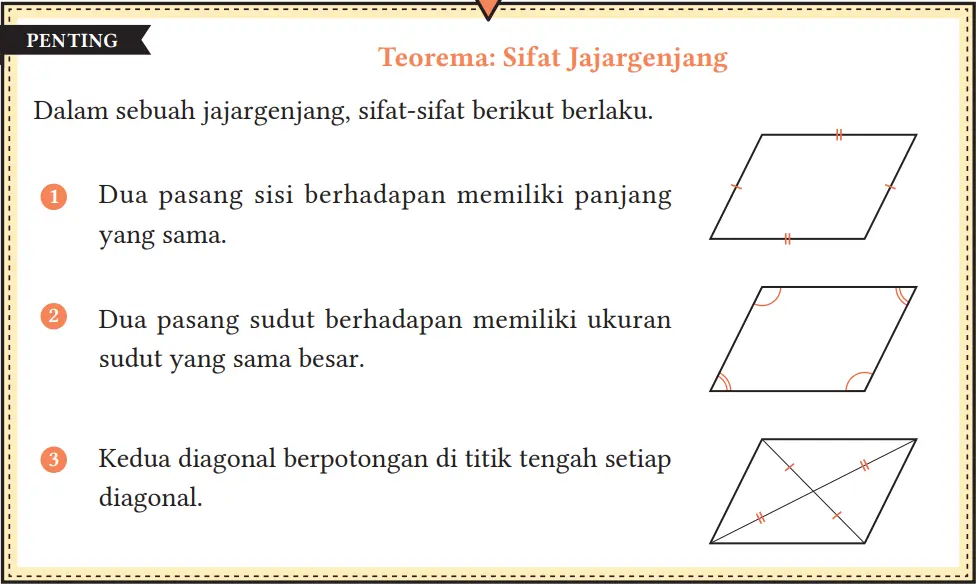
Hal-hal yang sudah kita selidiki sejauh ini dapat dirangkum menjadi sebuah teorema berikut.
Soal 5
Pada jajargenjang ABCD pada gambar-gambar berikut, carilah nilai dari x dan y.
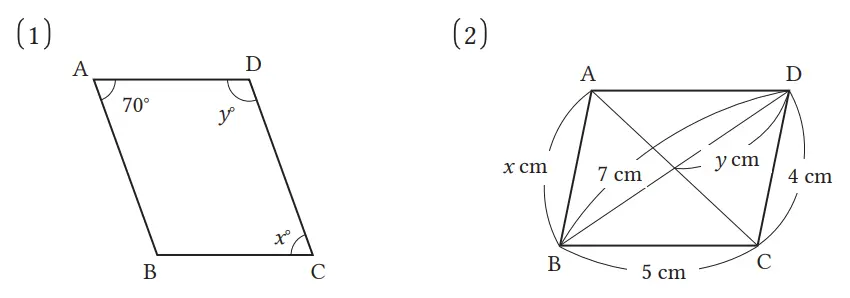
Jawaban:
(1) x = 70, y = 110
(2) x = 4, y = 3,5
Dengan menggunakan sifat-sifat jajargenjang, mari kita buktikan sifat-sifat bangun geometri berikut.
Contoh 2
Jika titik E dan F terletak pada diagonal AC dari ABCD sehingga AE = CF, maka buktikan bahwa BE = DF.
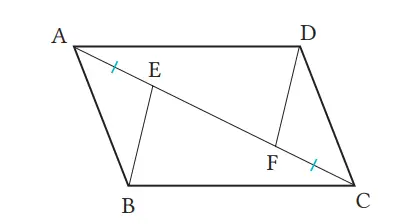
Bukti
Pada ∆ABE dan ∆CDF, berdasarkan yang diketahui, AE = CF ①
Sudut-sudut dalam berseberangan dari garis sejajar adalah sama besar. Karena AB // DC,
maka ∠BAE = ∠DCF ②
Karena sisi-sisi berhadapan pada jajargenjang adalah sama panjang,
maka AB = CD ③
Dari ①, ②, dan ③, dan berdasar aturan kekongruenan Sisi-Sudut-Sisi,
maka ∆ABE ≅ ∆CDF.
Dengan demikian, BE = DF.
Soal 6
Dari ∆ABE ≅ ∆CDF yang dibuktikan di Contoh 2 , apa yang dapat kita amati selain BE = DF? Jelaskan!
Jawaban:
(Contoh)
∠ABE = ∠CDF
∠AEB = ∠CFD
Penjelasan:
Sudut bersesuaian dari dua bangun yang kongruen adalah sama.
Soal 7
Buatlah garis yang melalui titik O yang merupakan titik potong kedua diagonal ABCD, dan misalkan P dan Q secara berturut-turut adalah titik-titik potong garis AD dan BC. Jawablah setiap pertanyaan berikut.
(1) Buatlah gambarnya.
Jawaban:
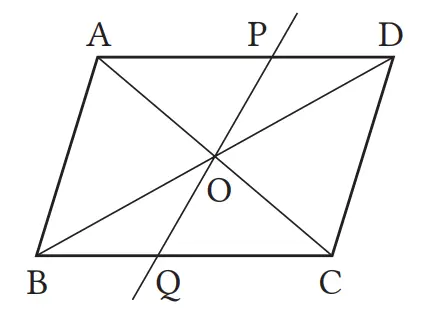
(2) Ruas garis mana yang mempunyai panjang yang sama dengan segmen PO?
Jawaban:
Garis bagi QO
(3) Buktikan pernyataan yang kamu selidiki di bagian (2).
Jawaban:
Karena sudut dalam berseberangan pada garis sejajar pada ΔAOP dan ΔCOQ, dan AD // BC, maka ∠PAO = ∠QCO ①
Sebab garis diagonal jajargenjang berpotongan di titik tengahnya, maka AO = CO ②
Karena sudut bertolak belakang, ∠AOP = ∠COQ ③
Dari (1), (2), dan (3), dan menurut aturan kekongruenan sudut-sisi-sudut, maka
ΔAOP ≅ ΔCOQ
Oleh karena itu, PO = QO.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
