ohgreat.id-Jawaban Kekongruenan Segitiga Siku-Siku halaman 145 Segitiga Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 145. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 5 Segitiga dan Segi Empat. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Kekongruenan Segitiga Siku-Siku
Q. Pada ∆ABC dan ∆DEF, jika
∠C = ∠F = 90°
AB = DE
∠B = ∠E
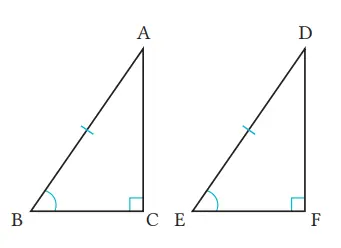
dapatkah kita menyatakan bahwa ∆ABC ≅ ∆DEF? Jelaskan!
Jawaban:
Dapat dikatakan ΔABC ≅ ΔDEF
Penjelasan:
Jumlah sudut dalam segitiga adalah 180° dan dari ∠C = ∠F serta ∠B = ∠E, maka ∠A = ∠D.
Oleh karena itu, dapat dikatakan bahwa “Dua sisi dan sudut pada kedua ujungnya masing-masing sama besar”. Jadi, ΔABC ≅ ΔDEF.
Syarat Kekongruenan “Sisi Miring dan Sisi Lain”
Dalam segitiga secara umum, meskipun “dua sisi dan satu sudut”-nya masing-masing sama, tidak dapat dikatakan kedua segitiga adalah kongruen. Namun, ketika salah satu sudut pada kedua segitiga adalah siku-siku, maka syarat kekongruenan “sisi miring dan sisi lain” terpenuhi.
Soal 1
Dengan mengacu pada gambar di bagian akhir halaman sebelumnya, jawablah pertanyaan berikut.
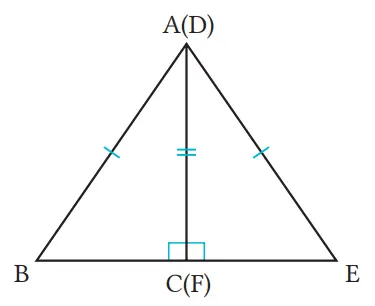
(1) Pada ∆ABC, tuliskan alasan kenapa ∠C = ∠F.
Jawaban:
Karena ΔABE adalah segitiga sama kaki dengan AB = AE, maka sudut ∠B dan ∠E adalah sama.
(2) Dengan menggunakan 1 , buktikan bahwa ∆ABC ≅ ∆AEC.
Jawaban:
Dari asumsi dalam ΔABC dan ΔAEC
∠ACB = ∠ACE = 90° ①
AB = AE ②
Dari ⑴, ∠B = ∠E ③
Dari (1), (2), dan (3), serta aturan kekongruenan sudut-sisi-sudut, maka ΔABC ≅ ΔAEC
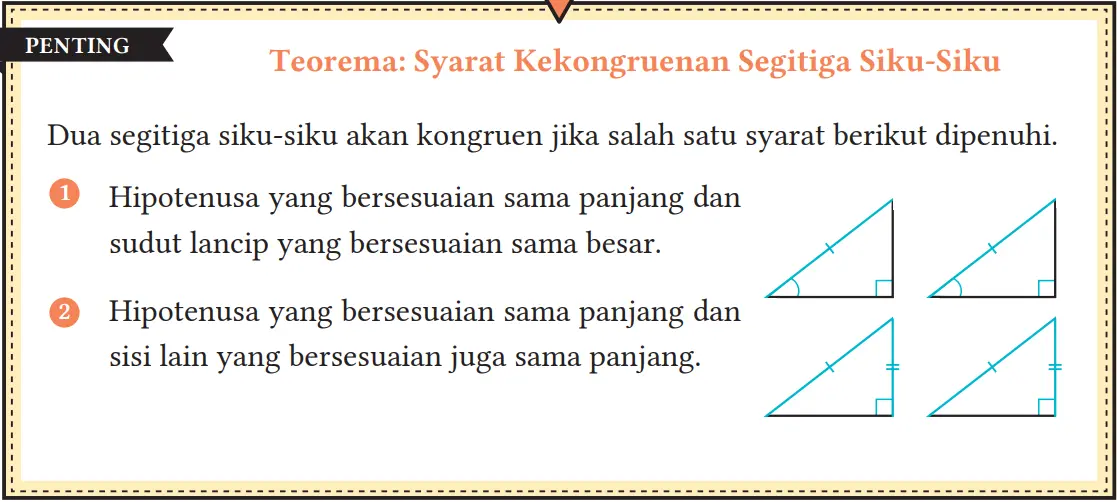
Hal yang sudah kita pelajari sejauh ini dapat dirangkum ke dalam sebuah teorema berikut.
Soal 2
Pada gambar-gambar berikut, pasangan-pasangan segitiga manakah yang kongruen? Nyatakan kekongruenan dengan simbol ≅. Tentukan juga syarat kekongruenan yang dipenuhi.
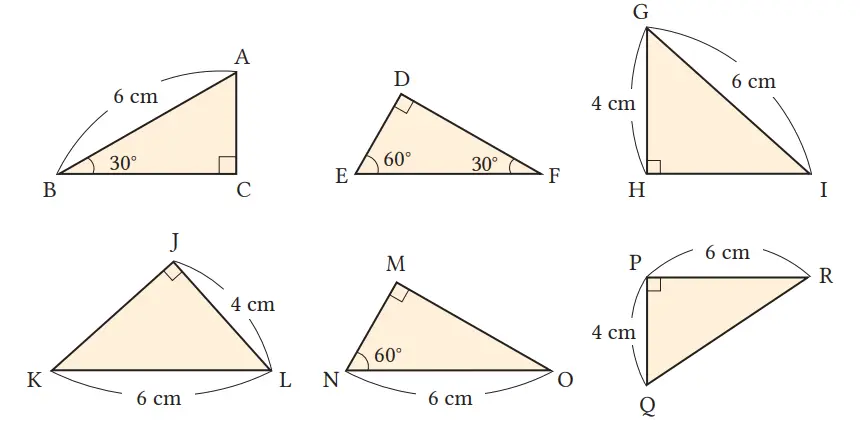
Jawaban:
ΔABC ≅ ΔNOM
Sisi miring dari segitiga siku-siku dan satu sudut lancip masing-masing adalah sama.
ΔGHI ≅ ΔLJK
Sisi miring segitiga siku-siku panjangnya sama dan sisi lainnya juga memiliki panjang sama.
Dengan menggunakan syarat kekongruenan segitiga siku-siku, marilah kita buktikan sifat bangun geometri.
Contoh 1
Dari titik P yang terletak pada garis bagi OZ dari ∠XOY, buatlah dua garis tegak lurus ke sisi OX dan OY, dan misalkan secara berturut-turut A dan B adalah titik potongnya. Buktikan bahwa PA = PB.
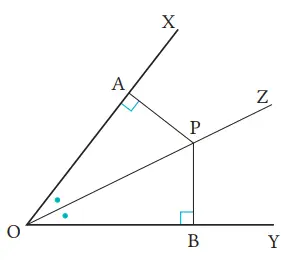
Cara
Dengan menggunakan PA ⊥ OX, PB ⊥ OY, tunjukkan bahwa dua segitiga yang terbentuk adalah kongruen, kemudian simpulkan bahwa PA = PB.
Bukti
Pada ∆AOP dan ∆BOP, berdasarkan yang kita ketahui,maka ∠PAO = ∠PBO = 90° ①
∠AOP = ∠BOP ② dan OP merupakan sisi yang sama ③
Dari ①, ②, dan ③, karena kedua segitiga siku-siku memiliki panjang hipotenusa yang bersesuaian sama panjang dan sudut lancip yang bersesuaian sama besar, maka ∆AOP ≅ ∆BOP.
Dengan demikian, PA = PB.
Soal 3
Dari pembuktian di Contoh 1, apa saja sifat garis bagi sudut yang dapat ditemukan? Jelaskan dengan kata, bukan dengan simbol!
Jawaban:
Semua titik pada garis bagi sudut berjarak sama dari kedua sisi sudut tersebut.
Soal 4
Pada hipotenusa AC dari segitiga siku-siku ABC dengan ∠B = 90°, ambil titik D yang memenuhi AB = AD, gambar sebuah garis yang melalui D dan tegak lurus AC serta memotong sisi BC dengan memisalkan titik potongnya adalah E. Buktikan bahwa BE = DE.
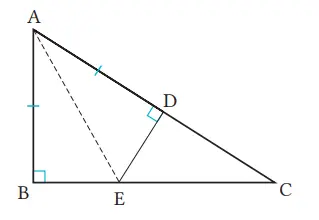
Jawaban:
Titik A dihubungkan ke titik E.
Dari asumsi di ΔABE dan ΔADE,
∠ABE = ∠ADE = 90° ①
AB = AD ②
AE sisi persekutuan ③
Dari (1), (2), dan (3), dan aturan kekongruenan dua sudut siku-suku, maka ΔABE ≅ ΔADE
Jadi, BE = DE.
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***