ohgreat.id-Jawaban Cara Membuktikan Sifat Bangun Geometri halaman 122 Kekongruenan Bangun-Bangun Geometri Matematika SMP Kelas 8 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 8 halaman 107. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 8 Kurikulum Merdeka Bab 4 Menyelidiki Sifat-Sifat Bangun Geometri. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Kekongruenan Bangun-Bangun Geometri
Cara Membuktikan Sifat Bangun Geometri
Soal 1
Tentukan bagian pengandaian dan kesimpulan untuk tiap pernyataan berikut.
(1) Jika ∆ABC ≅ ∆DEF, maka AB = DE.
(2) Pada ∆ABC, jika ∠A = ∠90°, maka ∠B + ∠C = 90°.
(3) Jika dua bilangan bulat a dan b adalah ganjil, maka a + b adalah bilangan genap.
Jawaban:
(1) ⟨Pengandaian⟩ ΔABC ≅ Δ DEF
⟨Kesimpulan⟩ AB = DE
(2) ⟨Pengandaian⟩ ΔABC, ∠A = 90°
⟨Kesimpulan⟩ ∠B + ∠C + 90°
(3) ⟨Pengandaian⟩ Dua bilangan bulat a dan b adalah bilangan ganjil
⟨Kesimpulan⟩ a + b adalah bilangan genap
Soal 2
Nyatakan pernyataan berikut dengan gambar, dan tentukan bagian pengandaian dan kesimpulannya.
Diketahui ruas garis AB dan CD berpotongan di titik M, jika AC//DB dan AM = BM, maka CM = DM.
Jawaban:
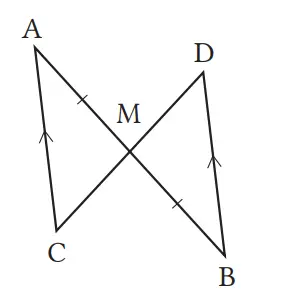
⟨Pengandaian⟩ AC//DB, AM = BM
⟨Kesimpulan⟩ CM = DM
Saat membuat gambar dari pernyataan bersyarat seperti ini, ajarkan peserta didik untuk memperhatikan poin-poin berikut.
(1) Saat menggambar segitiga, segi empat, dan lain-lain, gambarlah gambar umum, bukan gambar khusus seperti segitiga sama kaki dan persegi.
(2) Saat setiap peserta didik menunjukkan masalah dalam gambar, belum tentu gambarnya sama.
Cara Menulis Pembuktian
Membedakan antara pengandaian dan kesimpulan, serta menyusun proses pembuktian dari sifat-sifat bangun geometri.
Contoh 2
Seperti ditunjukkan pada gambar kanan bawah, dengan diketahui ruas garis AB dan CD berpotongan di titik M, buktikan bahwa jika AC // DB dan AM = BM, maka CM = DM.
Cara
Pengandaiannya adalah AC // DB dan AM = BM. Kesimpulannya adalah CM = DM. Agar dari pengandaian sampai pada kesimpulan, maka kita perlu menunjukkan kekongruenan antara ∆AMC dan ∆BMD.
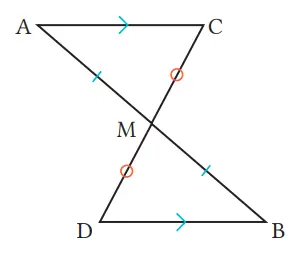
Bukti
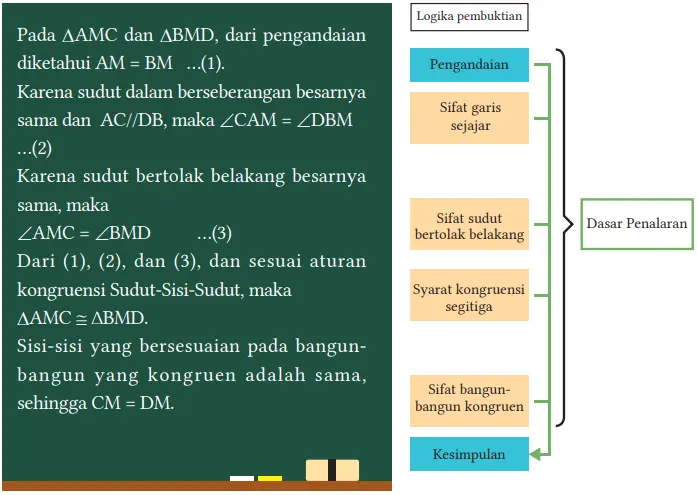
Ketika kita membuktikan sifat-sifat bangun geometri, kita gunakan proses berikut.
1) Gambar bangun geometri dengan benar, termasuk tanda dan huruf.
2) Bedakan antara pengandaian dan kesimpulan.
3) Dari pengandaian, kita berusaha sampai ke kesimpulan dengan menggunakan dasar penalaran.
Soal 3
Pada pembuktian di Contoh 2 di halaman 124, kita telah menunjukkan bahwa ∆AMC ≅ ∆BMD. Dari hasil ini, apa yang dapat kamu amati selain CM = DM?
Jawaban:
AC = BD
Soal 4
Pada gambar di kanan, jika AB = DC dan ∠ABC = ∠DCB, maka ∠BAC = ∠CDB. Jawab pertanyaan berikut.
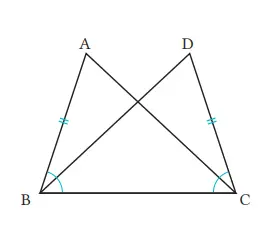
(1) Tentukan bagian pengandaian dan kesimpulan.
Jawaban:
⟨Pengandaian⟩ AB = DC, ∠ABC = ∠DCB
⟨Kesimpulan⟩ ∠BAC = ∠CDB
(2) Buktikan!
Jawaban:
Di ΔABC dan ΔDCB
Dari pengandaian tersebut, AB = DC ①
∠ABC = ∠DCB ②
karena merupakan sisi yang sama, maka BC = CB ③
Dari ①, ②, ③, karena 2 pasang sisi dan sudut di antara keduanya sama, maka ΔABC ≅ ΔDCB
Karena sudut bersesuaian dari bentuk kongruen adalah sama, maka∠BAC = ∠CDB
Soal 5
Kita konstruksi garis bagi OC dari ∠XOY seperti pada gambar di kanan. Isilah [] dan buktikan bahwa sinar garis OC adalah garis bagi sudut ∠XOY.
Jawaban:
(1) OB,
(2) OC
(3) ∠BOC
(4) OB
(5) BC
(6) OC
(7) sisi 3 pasang adalah
(8) ∠BOC
Soal 6
Gambar berikut menunjukkan metode pengkonstruksian ∠DAB yang kongruen dengan ∠XOY. Hal tersebut dapat dikonstruksi dengan pertama-tama membuat sinar garis AB, kemudian mengikuti proses (1) sampai (5). Jawablah pertanyaan berikut.
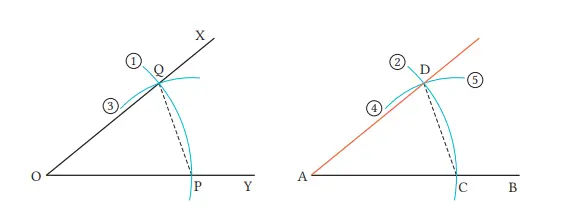
(1) Buat ∠XOY sembarang, dan konstruksi ∠DAB kongruen dengannya mengikuti proses di atas.
(2) Kita akan buktikan bahwa konstruksi ini benar. Jawablah pertanyaan berikut
1) Tentukan bagian pengandaian dan kesimpulan.
Jawaban:
⟨Pengandaian⟩ OP = AC, OQ = AD, PQ = CD
⟨Kesimpulan⟩ ∠XOY = ∠DAB
2) Untuk memperoleh pengandaian dari kesimpulan, segitiga-segitiga manakah yang perlu ditunjukkan kekongruenannya?
Jawaban:
ΔQOP dan ΔDAC
3) Buktikan!
Jawaban:
Dalam ΔQOP dan ΔDAC
Dari asumsi tersebut,
OP = AC ①
OQ = AD ②
PQ = CD ③
Dari ①, ②, ③, karena 3 pasang sisi sama satu sama lain, maka ΔQOP ≅ ΔDAC
Karena sudut bersesuaian dari bangun kongruen adalah sama, maka ∠QOP = ∠DAC sehingga ∠XOY = ∠DAB
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
