ohgreat.id-Jawaban Soal Ringkasan halaman 227 Luas Permukaan dan Volume Bangun Ruang Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 227. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 6 Bangun Ruang. Selanjutnya pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Soal Ringkasan

Gagasan Utama

1. Isilah [] dengan bilangan atau kata-kata yang tepat.

(1) Bangun ruang yang tersusun atas bidang-bidang disebut [] .

(2) Jika garis-garis tidak berpotongan pada ruang, dan mereka berada dalam satu bidang, maka [] mereka . Jika mereka tidak berada dalam satu bidang, maka mereka [] .

(3) Rasio keliling dinyatakan dalam huruf Yunani [].

(4) Panjang keliling lingkaran berjari-jari r cm adalah cm, dan luasnya adalah [] cm²
.
Jawaban:

(1) Bangun ruang yang tersusun atas bidang-bidang disebut [Polihedron]

(2) Jika garis-garis tidak berpotongan pada ruang, dan mereka berada dalam satu bidang, maka [berpotongan] mereka . Jika mereka tidak berada dalam satu bidang, maka mereka [bersilangan].

(3) Rasio keliling dinyatakan dalam huruf Yunani [π].

(4) Panjang keliling lingkaran berjari-jari r cm adalah [2πr] cm, dan luasnya adalah [2r²] cm²

2. Berdasarkan gambar prisma di samping ini, tentukan:

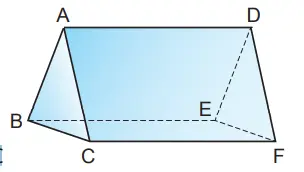
(1) Rusuk yang sejajar dengan sisi AD

Jawaban:

rusuk BC, EF

(2) Rusuk yang bersilangan dengan garis AD

Jawaban:

rusuk BC, EF

(3) Permukaan yang sejajar dengan permukaan ABC

Jawaban:

Bidang DEF

(4) Permukaan yang tegak lurus permukaan ABC

Jawaban:

Bidang ABED, BCFE, ACFD

3. Proyeksi bangun ruang ditunjukkan di samping ini. Lengkapilah proyeksi dengan menambahkan garis-garis yang sesuai.

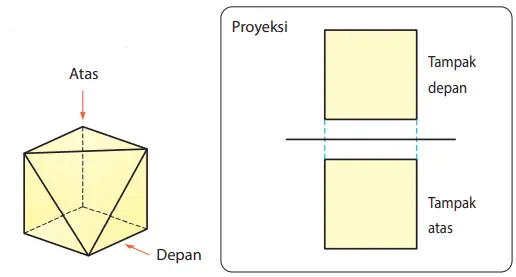
Jawaban:

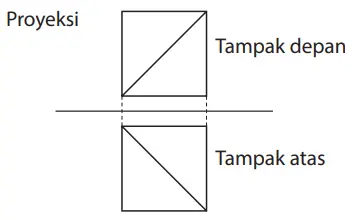
4. Tentukan luas permukaan dan volume bangun ruang di bawah ini.

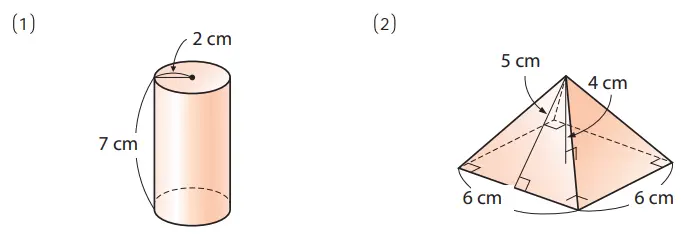
Jawaban:

(1) Luas permukaan = (2π × 2)× 7 + (π × 2²)× 2
= 28π + 4π × 2
= 36π (cm²)

Volume = (π × 2²) × 7 = 28π (cm³)

(2) Luas permukaan = {1/2 x 6 x 5} × 4 + 6²
= 60 + 36
= 96 (cm²)

Volume = 1/3 × 6² × 4
= 48 (cm³)

5. Sebuah bangun ruang dibentuk dengan memutar ΔABC sekali putar dengan sumbu putar garis AC, seperti ditunjukkan pada gambar di samping. Jawablah pertanyaan berikut ini.

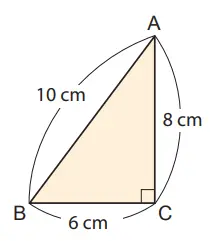
(1) Gambarlah sketsa bangun ruang tersebut.

Jawaban:

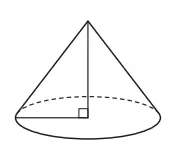
(2) Hitunglah volumenya.

Jawaban:

1/3 × (π × 6²) × 8= 96π (cm³)

(3) Hitunglah luas selimut.

Jawaban:

π × 10² × {(2π x 6)/(2π x 10)} = 60π (cm²)

6. Gambar di samping kanan ini menunjukkan jaring-jaring kubus. Sebuah kubus dibentuk dari jaring-jaring tersebut. Tentukan:

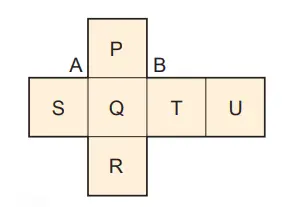
(1) Permukaan yang sejajar dengan permukaan P.

Jawaban:

permukaan (bidang) atau sisi R

(2) Permukaan yang sejajar dengan sisi A.

Jawaban:

permukaan (bidang) atau sisi R, U

(3) Permukaan yang tegak lurus dengan rusuk AB.

Jawaban:

permukaan (bidang) atau sisi S, T

7. Tentukan luas permukaan da volume bangun ruang berikut.

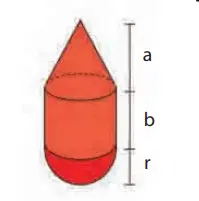
Jawaban:

πr²(2/3r + b + 1/3a)

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Selanjutnya jangan lewatkan dan dapatkan Berita berita Update lainnya.***