ohgreat.id-Jawaban Soal Menyederhanakan Bentuk Linear halaman 77 Menyederhanakan Bentuk Aljabar Matematika SMP Kelas 7 Kurikulum Merdeka.
Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 77. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 2 Aljabar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???
Menyederhanakan Bentuk Aljabar
Menyederhanakan Bentuk Linear
Penjumlahan dan Pengurangan dalam Bentuk Linear
Q. Ketika pita kakak sepanjang a cm saya potong, maka pitanya berkurang 7 cm. Ketika saya memotong pita adik sebanyak dua potong masing-masing sepanjang a cm, maka pitanya tinggal 5 cm.
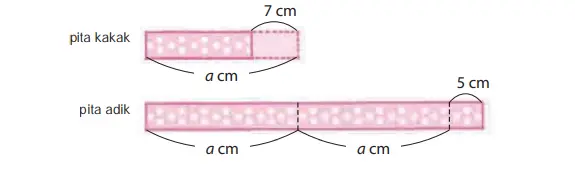
(1) Berapakah panjang pita kakak digabungkan dengan pita adik mula-mula?
Jawaban:
(3a – 2) cm
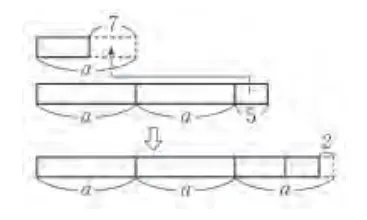
(2) Berapa cm pita adik lebih panjang dari pita kakak?
Jawaban:
(a + 12) cm
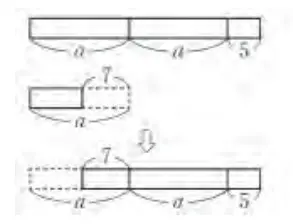
Contoh 1
(a – 7) + (2a + 5)
= a – 7 + 2a + 5
= a + 2a – 7 + 5 = 3a – 2
Ketika menambahkan dua bentuk aljabar linear, gabungkan suku-suku yang memuat huruf yang sama. Demikian juga suku-suku bilangan. Tujuannya adalah untuk menyederhanakan bentuk aljabar tersebut.
1. Sederhanakanlah.
(1) (5x – 4) + (3x – 6)
(2) (2x + 9) + (4x – 3)
(3) (3a + 5) + (-2a + 8)
(4) (-7a – 1) + (a + 4)
(5) (-7 + 5x) + (2 – 5x)
(6) （3/5x – 2/3）+（2/5x + 1/3 )
Jawaban:
(1) 8x – 10
(2) 6x + 6
(3) a + 13
(4) -6a + 3
(5) -5
(6) x -1/3
Contoh 2
Sederhanakanlah (2a + 5) – (a – 7).
Ubahlah tanda negatif pada a – 7, Kemudian jumlahkan dengan bentuk aljabar linear lain.
(2a + 5) – (a – 7)
= (2a + 5) + (-a + 7)
= 2a + 5 – a + 7 = a + 12
Jawab: a + 12
Ketika mengurangkan bentuk aljabar linear, ubahlah tanda dari pengurang, kemudian jumlahkan pada suku linear lainnya.
2. Sederhanakanlah.
(1) (7x + 2) – (3x – 1)
(2) (x – 8) – (2x – 5)
(3) (-4a + 9) – (a + 3)
(4) (5a + 6) – (-2a + 6)
(5) (7 – x) – (2x + 8)
(6) （1/3x – 2) –（1/2x – 5)
Jawaban:
(1) 4x + 3
(2) -x – 3
(3) -5a + 6
(4) 7a
(5) -3x – 1
(6) -1/6x+3
Perkalian Bentuk Aljabar dan Bilangan
Q. Terdapat 5 orang yang masing-masing menerima 4 buah kotak berisi kelengkeng. Tiap kota tersebut berisi seberat a gram kelengkeng. Nyatakan berat total kelengkeng (yang diterima 5 orang) tersebut. Pastikan berat kotak tidak dihitung.
Jawaban:
(4a × 5)g, (4a + 4a + 4a + 4a + 4a) g, 20a g
3. Sederhanakanlah.
(1) 6x × 2
(2) (-7) × 2y
(3) -3a × 4
(4) -b × (-9)
(5) 10 × 0,8x
(6) 2/3a × 6
Jawaban:
(1) 12x
(2) -14y
(3) -12a
(4) 9b
(5) 8x
(6) 4a
Contoh 4
Sederhanakanlah 2(x + 4).
hapus tanda kurung dengan menerapkan sifat distributif.
2(x + 4)
= 2 × x + 2 × 4
= 2x + 8 Jawab: 2x + 8
4. Sederhanakanlah.
(1) 5(x + 2)
(2) -2(4x + 5)
(3) (1 – 6x) × 3
(4) (a – 4) × (-6)
(5) -(-9x + 8)
(6) 2/3(9y + 6)
Jawaban:
(1) 5x + 10
(2) -8x – 10
(3) 3 – 18x
(4) -6a + 24
(5) 9x – 8
(6) 6y + 4
5. Sederhanakanlah.
(1) (3x + 1)/2 × 4
(2) 12 x (x – 3)/4
Jawaban:
(1) Jadi = (3x + 1) × 2
= 6x + 2
(2) Jadi = 3 × (x – 3)
= 3x – 9
Pembagian Bentuk Aljabar dengan Bilangan
Contoh 7
Sederhanakanlah 6x : 4.
6. Sederhanakanlah.
(1) 8x : 2
(2) 12x : (-4)
(3) -10x : (-5)
(4) -a : 5
(5) 9x : 12
(6) 15x : (-3/2)
Jawaban:
(1) 4x
(2) -3x
(3) 2x
(4) -a/5 atau -1/5a
(5) 3.4x atau 3x/4
(6) -10x
7. Sederhanakanlah.
(1) (2x + 6) : 2
(2) (12a – 8) : (-4)
(3) (10x – 5) : 5/2
Jawaban:
(1) x + 3
(2) -3a + 2
(3) 4x – 2
8. Ilzar mengubah (8x – 3) : 2 ke dalam pecahan seperti ditunjukkan di samping ini. Apakah yang dilakukan Ilzar benar? Koreksilah kesalahannya jika ada.
Benarkah?
(8x – 3) : 2
= (8x – 3)/2
= 4x -3
Jawaban:
Tidak benar
(8x – 3) : 2
= (8x – 3)/2
= 8x/2 – 3/2 = 4x – 3/2
9. Sederhanakanlah.
(1) (6x + 1) + 3(x + 2)
(2) 2(-a + 6) + 4(a – 3)
(3) -3(3x – 5) + 7(2x – 1)
(4) 2(a + 5) – 8(a + 1)
(5) 6(x – 2) – 2(3x – 7)
(6) -(a – 8) – 5(-2a + 4)
Jawaban:
(1) 9x + 7
(2) 2a
(3) 5x + 8
(4) -6a + 2
(5) 2
(6) 9a – 12
10. Sederhanakanlah.
(1) 1/2(6x + 4) + (6x – 3)
(2) 2/3(9a – 6) – 1/2(2a – 10)
Jawaban:
(1) 5x + 1
(2) 5a + 1
Cermati
Apa Pengertian Suku Aljabar Kuadrat dan Bentuk Aljabar Kuadrat?
Suku-suku yang menyatakan hasil kali dua huruf dan bilangan seperti 2×2 atau -5a2b disebut suku aljabar kuadrat. Bentuk aljabar yang memuat suku kuadrat disebut bentuk aljabar kuadrat
Disclaimer:
1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya
2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama
3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain
*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***
