ohgreat.id-Jawaban Soal Bentuk Aljabar Linear halaman 75 Menyederhanakan Bentuk Aljabar Matematika SMP Kelas 7 Kurikulum Merdeka.

Kali ini, Ohgreat akan membahas jawaban Matematika SMP Kelas 7 halaman 75. Pertanyaan ini bisa Adik-adik temukan pada buku Matematika SMP Kelas 7 Kurikulum Merdeka Bab 2 Aljabar. Pembahasan berikut bisa Adik-adik simak untuk mencocokan dengan jawaban yang telah Ohgreat kerjakan sebelumnya. Jadi, silahkan kerjakan terlebih dahulu secara mandiri ya???

Menyederhanakan Bentuk Aljabar

Bentuk Aljabar Linear

Q. Nyatakanlah luas tiga persegi panjang pada gambar di samping ini dengan menggunakan bentuk aljabar. Hitunglah selisih luas antara dua gambar di (1) dan (2)

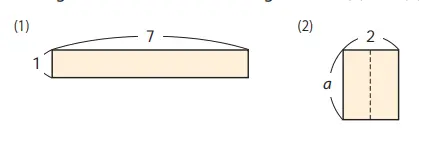
Jawaban:

Luas persegi panjang 3a

(1) 3a – 7

(2) 3a – 2a

Selisih luas persegi panjang di Q jika dibandingkan dengan 1 dapat dinyatakan sebagai 3a – 7. Dengan menggunakan tanda +, pernyataan tersebut dapat dituliskan sebagai 3a + (-7), 3a dan 7 disebut suku-suku. Pada suku 3a, bilangan 3 disebut koefisien dari a.

Contoh
Karena -2x – 5 = -2x + (-5), maka suku-suku pada bentuk aljabar -2x – 5 adalah -2x dan -5. Koefisien dari x pada suku -2x adalah -2.

1. Sebutkanlah suku-sukunya. Tentukan koefisien dari huruf-huruf pada bentuk aljabar berikut ini.

(1) 5a – 20

(2) -9a + 8

(3) 4 – x

(4) x/2 + 7

Jawaban:

(1) Sukunya adalah 5a dan -20.
Koefisien a dari suku 5a adalah 5.

(2) Sukunya adalah -9a dan 8.
Koefisien a dari suku -9a adalah -9.

(3) Sukunya adalah 4 dan –x.
Koefisien x dari suku –x adalah -1.

(4) Sukunya adalah x/2dan 7
Koefisien dari x dari suku x/2 adalah 1/2.

2. Berdasarkan Q, di atas, bandingkan luas (3) dengan luas (2) dan nyatakanlah selisih luas tersebut menggunakan bentuk aljabar. Sebutkan suku-sukunya. Untuk suku dengan huruf, sebutkan koefisiennya.

Jawaban:

Selisih luasnya adalah 3a – 2a.
Sukunya adalah 3a dan -2a.
Koefisien a dari suku 3a adalah 3.
Koefisien a dari suku -2a adalah -2.

Ketika terdapat suku-suku dengan huruf yang sama seperti pada Soal 2 di halaman 75, kita dapat menerapkan sifat distributif untuk menggabungkan suku-suku dengan huruf yang sama.
3a – 2a = (3 – 2)a = a

3. Sederhanakan.

(1) 5x + 2x

(2) 9a – 6a

(3) -7b + b

(4) -y – 4y

(5) 0,4x + 0,6x

(6) 4/5a – 1/5 a

Jawaban:

(1) 7x (4) -5y

(2) 3a (5) x

(3) -6b (6) 3/5a

4. Sederhanakanlah.

(1) 4x + 7 + 5x + 8

(2) -3a + 5 + 9a – 2

(3) 2x – 12 – 6x + 15

(4) -a + 2 – 3 – 8a

Jawaban:

(1) 9x + 15

(2) 6a + 3

(3) -4x + 3

(4) -9a – 1

Suku yang dinyatakan sebagai hasil kali satu huruf dan bilangan positif atau negatif seperti 2x atau -8adisebut suku linear.

5. Manakah yang merupakan bentuk aljabar linear?

a. -8x

b. x2 + 1

c. 2a + 8

d 2/5a – 7

Jawaban:

(a), (c), dan (d)

Dalam bentuk aljabar linear ax + b ( a ≠ 0), ingatlah bahwa ax + b dengan b ≠ 0 dan axdengan b = 0 .

 

 

Disclaimer:

1. Kunci jawaban pada unggahan Ohgreat tidak mutlak kebenarannya

2. Unggahan ini bisa Adik-adik gunakan sebagai salah satu acuan dalam mengerjakan soal bukan sebagai acuan utama

3. Jawaban pada unggahan Ohgreat mungkin akan berbeda dengan pembahasan di sekolah atau penunjang lain

*** Agar tidak ketinggalan update berita berita menarik dan Pembahasan Soal terbaru lainnya yang ada di ohgreat.id. Jangan lewatkan dan dapatkan Berita berita Update lainnya.***